Xét dấu biểu thức sau: f(x) = (4x - 1)(x + 2)(3x - 5)(-2x + 7)

Những câu hỏi liên quan
Xét dấu các biểu thức sau:
a) f(x)= (x-2).(x+1)/3x -1
b) f(x)= 1-4x /2x-3
c) f(x)= 3x (6 -2x)/5x-4
d) f(x)= -4/3x+1 - 3/2-x
e) f(x)= 2x-5/(3x+1) (2-4x)
Xem chi tiết
Bài 3: Xét dấu các biểu thức sau 1/ f(x) = (2x - 1)(x ^ 3 - 1)
. 2 / (f(x)) = (- 2x ^ 2 + 7x + 7)/(x ^ 2 - 3x - 10) - 1
Xét dấu các biểu thức sau :
\(f\left(x\right)=\left(4x-1\right)\left(x+2\right)\left(3x-5\right)\left(-2x+7\right)\)
Xét:
\(4x-1=0\Leftrightarrow x=\dfrac{1}{4}\); \(x+2=0\Leftrightarrow x=-2\);
\(3x-5=0\Leftrightarrow x=\dfrac{5}{3}\); \(-2x+7=0\Leftrightarrow x=\dfrac{7}{2}\).
Vậy: \(f\left(x\right)=0\) khi \(x=\left\{-2;-\dfrac{1}{4};\dfrac{5}{3};\dfrac{7}{2}\right\}\).
\(f\left(x\right)>0\) khi \(\left(-2;-\dfrac{1}{4}\right)\cup\left(\dfrac{5}{3};\dfrac{7}{2}\right)\).
\(f\left(x\right)< 0\) khi \(\left(-\infty;-2\right)\cup\left(-\dfrac{1}{4};\dfrac{5}{3}\right)\cup\left(\dfrac{7}{2};+\infty\right)\).
Đúng 0
Bình luận (0)
Xét dấu biểu thức:
a) f(x) = \(-3x^2+2x\)
b) g(x) = \(x^2-10x+25\)
c) h(x) = \(4x^2-4x+1\)
d) q(x) = ( 2x+3 ).( x- 5 )
a: Đặt f(x)=0
=>\(-3x^2+2x=0\)
=>\(3x^2-2x=0\)
=>x(3x-2)=0
=>\(\left[{}\begin{matrix}x=0\\3x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
Bảng xét dấu:
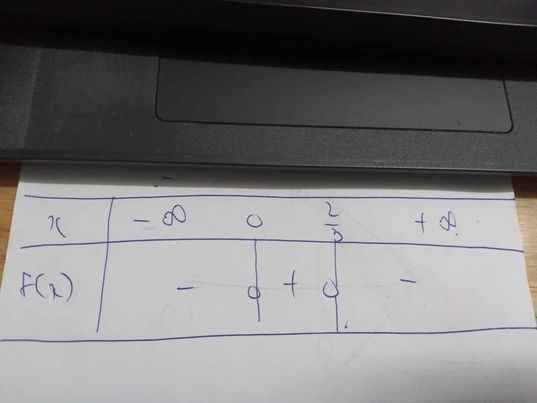
b: Đặt G(x)=0
=>\(x^2-10x+25=0\)
=>\(\left(x-5\right)^2=0\)
=>x-5=0
=>x=5
Bảng xét dấu:

c: Đặt H(x)=0
=>\(4x^2-4x+1=0\)
=>\(\left(2x-1\right)^2=0\)
=>2x-1=0
=>x=1/2
Bảng xét dấu:

d: Đặt Q(x)=0
=>(2x+3)(x-5)=0
=>\(\left[{}\begin{matrix}2x+3=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=5\end{matrix}\right.\)
Bảng xét dấu:

Đúng 0
Bình luận (0)
Xét dấu biểu thức sau đây:\(f\left(x\right)=\) \(\dfrac{2x+3}{x+1}+\dfrac{x+6}{-3x-2}\)
Lập bảng xét dấu các biểu thức sau :
a. \(f\left(x\right)=\left(3x^2-10x+3\right)\left(4x-5\right)\)
b. \(f\left(x\right)=\left(3x^2-4x\right)\left(2x^2-x-1\right)\)
c. \(f\left(x\right)=\left(4x^2-1\right)\left(-8x^2+x-3\right)\left(2x+9\right)\)
d. \(f\left(x\right)=\dfrac{\left(3x^2-x\right)\left(3-x^2\right)}{4x^2+x-3}\)
a) 3x^3 -10x+3 =(3x-1)(x-3)
| x | -vc | 1/3 | 5/4 | 3 | +vc | |||||||||
| 3x-1 | - | 0 | + | + | + | + | + | |||||||
| x-3 | - | - | - | - | - | 0 | + | |||||||
| 4x-5 | - | - | - | 0 | + | + | + | |||||||
| VT | - | 0 | + | 0 | - | 0 | + |
Kết luận
VT< 0 {dấu "-"} khi x <1/3 hoắc 5/4<x<3
VT>0 {dấu "+"} khi x 1/3<5/4 hoặc x> 3
VT=0 {không có dấu} khi x={1/3;5/4;3}
Đúng 0
Bình luận (0)
Xét dấu biểu thức sau: f(x,y)= 3x^2 + y^2 - 2x - xy + y +3
\(f\left(x;y\right)=3x^2+y^2-2x-xy+y+3\)
\(=\left(x^2-xy+\dfrac{y^2}{4}\right)+\dfrac{1}{2}\left(4x^2-4x+1\right)+\dfrac{1}{3}\left(\dfrac{9}{4}y^2+3y+1\right)+\dfrac{13}{6}\)
\(=\left(x-\dfrac{y}{2}\right)^2+\dfrac{1}{2}\left(2x-1\right)^2+\dfrac{1}{3}\left(\dfrac{3y}{4}+1\right)^2+\dfrac{13}{6}>0;\forall x;y\)
Đúng 0
Bình luận (0)
xét dấu các biểu thức sau:
a) f(x) =(2x-4)(3x+5)
Với \(x>2\) thì f(x) > 0.
Với \(x<\frac{-3}{5}\) thì f(x) > 0.
Với \(\frac{-3}{5}< x<2\) thì f(x) < 0.
Với x = 2 thì f(x) = 0.
Với \(x=\frac{-3}{5}\) thì f(x) = 0.
Đúng 1
Bình luận (0)
f(x)=(3x+1)/(x+1)-(4)/(x^(2)-2x+1)
Xét dấu biểu thức ạ ai giúp mình với

















