Biểu thức (cota + tana)2 bằng
A. 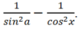
B. cot2a + tan2a.
C .![]()
D. cot2a.tan2a + 2.
3; cho tana-cota=3 . tính giá trị các biểu thức sau :
a; A= tan2a + cot2a
Biết sina = \(\frac{2}{5}\) . Tính giá trị biểu thức : \(\frac{cota-tana}{cota+tana}\)
Ta có : \(\sin^2a+\cos^2a=1\Rightarrow\cos a=\frac{\sqrt{21}}{5}\)
Ta có : \(\frac{\cot a-\tan a}{\cot a+\tan a}=\frac{\frac{\cos a}{\sin a}-\frac{\sin a}{\cos a}}{\frac{\cos a}{\sin a}+\frac{\sin a}{\cos a}}\\ =\frac{\frac{\frac{\sqrt{21}}{5}}{\frac{2}{5}}-\frac{\frac{2}{5}}{\frac{\sqrt{21}}{5}}}{\frac{\frac{\sqrt{21}}{5}}{\frac{2}{5}}+\frac{\frac{2}{5}}{\frac{\sqrt{21}}{5}}}=\frac{17}{25}=0,68\)
Cho cosa = 3/4 vào 270°<a<370° . Tính
A sina , tana , cota
B sin2a , cos2a , tan2a
B sin( a+ π\3 )
Chứng minh rằng giá trị của biểu thức A dưới đây không phụ thuộc vài số đo góc a
A=(tana + cota)bình phương - (tana-cota)bình phương
cho sin a= 1/3. Tính giá tị của biểu thức A= cota-tana/ tan+2cota
\(A=\dfrac{cota-tana}{tana+2\cdot cota}\)
\(=\dfrac{\dfrac{cosa}{sina}-\dfrac{sina}{cosa}}{\dfrac{sina}{cosa}+2\cdot\dfrac{cosa}{sina}}\)
\(=\dfrac{cos^2a-sin^2a}{sina\cdot cosa}:\dfrac{sin^2a+2\cdot cos^2a}{sina\cdot cosa}\)
\(=\dfrac{cos^2a-sin^2a}{sin^2a+2\cdot cos^2a}\)
\(=\dfrac{1-2\cdot sin^2a}{sin^2a+2\left(1-sin^2a\right)}\)
\(=\dfrac{1-2\cdot sin^2a}{-sin^2a+2}\)
\(=\dfrac{1-2\cdot\left(\dfrac{1}{3}\right)^2}{-\left(\dfrac{1}{3}\right)^2+2}=\dfrac{1-\dfrac{2}{9}}{-\dfrac{1}{9}+2}=\dfrac{7}{9}:\dfrac{17}{9}=\dfrac{7}{17}\)
câu20:Cho tana=-2 và pi/2<a<pi.Tính giá trị biểu thức P=cos2a+sin2a
câu21Cho 2tana-cota=1 và -pi/2<a<0.Tính giá trị của biểu thức P=tana+2cota
câu22: Cho sina=-1/7 và pi<a<3pi/2.Tính giá trị của biểu thức P=cos(a+pi/6)
câu23: Cho sina=-1/9; cosb=-2/3 và pi<a<3pi/2; pi/2<b<pi. Tính giá trị của biểu thức P= sin(a+b)
Rút gọn biểu thức: cota+ tana/ 1+ tan2a.tana
Chứng minh:
tan3a+tan2a+tana=tan3a*tan2a*tana
Chứng minh:
tan3a-tan2a-tana=tan3a*tan2a*tana
\(tan3a-tan2a-tana=\frac{sin3a}{cos3a}-\frac{sin2a}{cos2a}-\frac{sina}{cosa}=\frac{sin3a.cos2a-sin2a.cos3a}{cos3a.cos2a}-\frac{sina}{cosa}\)
\(=\frac{sin\left(3a-2a\right)}{cos3a.cos2a}-\frac{sina}{cosa}=\frac{sina}{cos3a.cos2a}-\frac{sina}{cosa}=tana\left(\frac{cosa}{cos3a.cos2a}-1\right)\)
\(=tana\left(\frac{cos\left(3a-2a\right)-cos3a.cos2a}{cos3a.cos2a}\right)=tana\left(\frac{cos3a.cos2a+sin3a.sin2a-cos3a.cos2a}{cos3a.cos2a}\right)\)
\(=tana\left(\frac{sin3a.sin2a}{cos3a.cos2a}\right)=tana.tan2a.tan3a\)