Cho hàm số y = ( a 2 – 4 ) x 2 + b – 3 a b + 2 a x – 2 là hàm số bậc nhất khi:
A. a = 2 ; b ≠ 6 ; − 4
B a = − 2 ; b ≠ − 6 ; 4
C. a = 2 ; a = − 2
D. Cả A, B đều đúng
1.Cho hàm số y = g(x) = x - 4. Khi đó g(-2) bằng
A.-2 B.2 C.-6 D.6
2.Cho hàm số y = f(x) = -3x+ 5. Nếu f(x) = -7 thì x bằng
A.2/3 B.-4 C.2 D.4
Câu 25. Cho hàm số \(y = \dfrac{x + 1}{x - 1}, y = -x^3+x^2-3x+1, y = x^4 + 2x^2 +2.\) Trong các hàm số trên, có bao nhiêu hàm số đơn điệu trên \(R\)?
A. 1. B. 3. C. 0. D. 2.
\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất
a) y= ( m - 2 )x - \(\dfrac{2}{3}\) b) y= ( 4 - 2022m )x - 2 c) y= \(\sqrt{1-2m}\)x + m - 3
Bài 2: Cho đồ thị hàm số y= -2x + 3
a) Xác định hệ số a,b
b) Các điểm A( -2 ; 7) ; B(\(\sqrt{2}\) ; 6)
c) Tìm tọa độ điểm M thuộc ( d ) có tung độ = 11
d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nó
e) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau
Bài 1 : Cho hàm số y=(m-3)x+4 . Với giá trị nào của m thì hàm số đồng biến, nghịch biến Bài 4: Cho hàm số y=(3-√2) x+1 a, Hàm số đồng biến hay nghịch biến? Vì sao? b, Tính các giá trị tương ứng của y khi x nhân các giá trị sau ; O, 1, √2, 3+√2, 3-√2
Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)
phần 1 -hệ phương trình / | 3 x - 4 y = 7 < | 2 x + Sy = -1 \ -hàm số và đồ thị của hàm số y = a x² Đồng biến nghịch biến tìm hệ số a vd : cho hàm số y = ax² (P) a, tìm a cho biết đồ thị hàm số đi qua A ( -3 ; 3 ) b, vẽ đồ thị hàm số với a vừa tìm được - giải bài toán bằng hệ phương trình - chứng minh tứ giác nội tiếp ( các điểm cùng thuộc 1 đường tròn ) - các góc bằng nhau . L là góc nội tiếp - chứng minh bất đẳng thức phương trình bặc nhất 2 ẩn ; nghiệm của phương trình a x + b y = c ( Xo ; Yo ) 2 hệ tương đương khi có cùng tập nghiệm hàm số đồng biến , nghịch biến và tìm hệ số điểm thuộc đồ thị vị trí tương đối của 2 đường tròn , đường tròn ngoại tiếp của tam giác tính chất 2 tiếp tuyến cắt nhau tứ giác nối tiếp - công thức nghiệm tam giác - một mảnh vườn hình chữ nhật có nhiều dài lớn hơn chiều rộng 6m ; mảnh vườn là 160 m² tìm cách kích thước của mảnh vườn
3:
Gọi chiều rộng là x
=>Chiềudài là x+6
Theo đề, ta có: x(x+6)=160
=>x^2+6x-160=0
=>(x+16)(x-10)=0
=>x-10=0
=>x=10
=>Chiều dài là 16m
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
1.cho hàm số bậc nhất: a/ y= -2 . (x+5) - 4 b/ y = phân thức 1+x phần 2
tìm hệ số a,b của hàm số bậc nhất đó
2. cho hàm số y =ax+5
a/ tìm a biết khi x = 1 thì y = 1
b/ với giá trị của a tìm được hãy hoàn thành bảng sau:
x = -2,-1,0,?, ?
y = ?,?,?,3,-7
3.vẽ đồ thị hàm số sau: a/ y =2x- 3 b/ y = -x+4 c/ y = -5/2x
Bài 2:
a: Thay x=1 và y=1 vào y=ax+5, ta được:
\(a\cdot1+5=1\)
=>a+5=1
=>a=-4
b: a=-4 nên y=-4x+5
| x | -2 | -1 | 0 | 1/2 | -3 |
| y=-4x+5 | 13 | 9 | 5 | 3 | -7 |
Bài 1:
a: \(y=-2\left(x+5\right)-4\)
\(=-2x-10-4\)
=-2x-14
a=-2; b=-14
b: \(y=\dfrac{1+x}{2}\)
=>\(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2};b=\dfrac{1}{2}\)
Bài 3:
a: Bảng giá trị:
| x | 1 | 3 |
| y=2x-3 | -1 | 3 |
Vẽ đồ thị
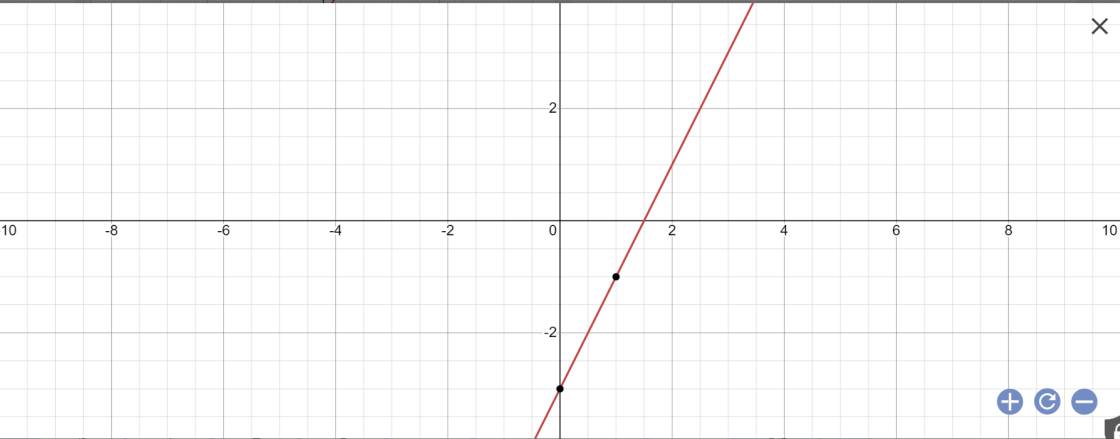
b: Bảng giá trị
| x | 1 | 3 |
| y=-x+4 | 3 | 1 |
Vẽ đồ thị
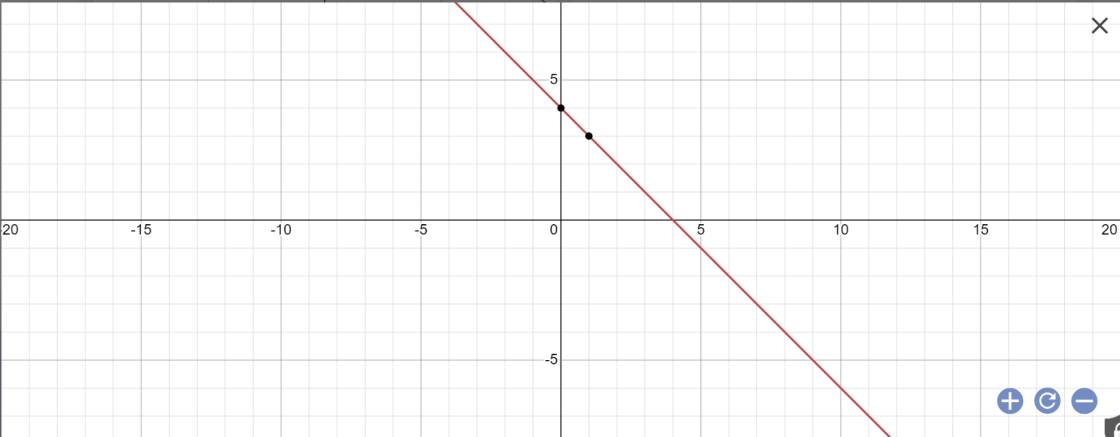
c: Bảng giá trị
| x | 0 | 6 |
| \(y=-\dfrac{5}{2}x\) | 0 | -15 |
Vẽ đồ thị:

a) Cho đồ thị hàm số (p) \(y=\dfrac{-x^2}{4}\)
và (d) \(y=\dfrac{-x}{2}-2\)
Giải bất phương trình sau bằng đồ thị hàm số trên
\(x^2-2x-8< 0\)
Cho hàm số y = f ( x ) có đồ thị như hình vẽ.
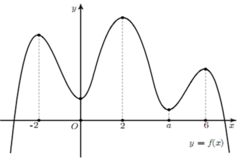
Biết tất cả các điểm cực trị của hàm số y = f ( x ) là – 2, 0, 2, a , 6 với 4 < a < 6. Số điểm cực trị của hàm số y = f ( x 6 − 3 x 2 ) là
A. 8
B. 11
C. 9
D. 7
Bài 1: Tìm m để a/ Hàm số y = (- m + 4) x + 5 là hàm số bậc nhất b/ Hàm số y = (2 - m) x - 3 đồng biến trong R Bài 2: Cho hàm số y = 2x có đồ thị (d1); hàm số y=x-1 có đồ thị (d2) . a / Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ. b/ Xác định tọa độ giao điểm A của (d1) và (d2) bằng phép toán. c/ Viết ph / trình đường thẳng (D) song song với (d2) và điểm M(6;3) qua
b: Để hàm số đồng biến thì 2-m>0
hay m<2