\(a,\\ \Leftrightarrow3x-x=10-6\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=2\\ b,\\ \Leftrightarrow\left(x-2\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

\(a,\Leftrightarrow3x-x=10-6\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=\dfrac{4}{2}=2\)

Vậy phương trình có tập nghiệm S = \(\left\{2\right\}\)

\(b,\Leftrightarrow\left(x+1\right)\left(x-2\right)=0\\ \Leftrightarrow x+1=0\)           hoặc            \(\Leftrightarrow x-2=0\)       

\(\Leftrightarrow x=-1\)                                                     \(\Leftrightarrow x=2\)

Vậy phương trình có tập nghiệm S = \(\left\{-1;2\right\}\)

a)3x + 6 = x +10
 ⟺3x-x=10-6
 ⟺2x=4 ⟺x=2
Vậy tập nghiệm của phương trình là S={2}
b) x(x + 1) - 2 (x + 1) = 0
 ⟺(x+1)(x-2)=0
 ⟺x+1=0        ⟺x=-1
     x-2=0         ⟺x=2
Vậy tập nghiệm của phương trình là S={2;-1}

a) \(\sqrt {2 - x}  + 2x = 3\)\( \Leftrightarrow \sqrt {2 - x}  = 3 - 2x\)  (1)

Ta có: \(3 - 2x \ge 0 \Leftrightarrow x \le \frac{3}{2}\)

Bình phương hai vế của (1) ta được:

\(\begin{array}{l}2 - x = {\left( {3 - 2x} \right)^2}\\ \Rightarrow 2 - x = 9 - 12x + 4{x^2}\\ \Leftrightarrow 4{x^2} - 11x + 7 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {TM} \right)\\x = \frac{7}{4}\left( {KTM} \right)\end{array} \right.\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ 1 \right\}\)

b) \(\sqrt { - {x^2} + 7x - 6}  + x = 4\)\( \Leftrightarrow \sqrt { - {x^2} + 7x - 6}  = 4 - x\)  (2)

Ta có: \(4 - x \ge 0 \Leftrightarrow x \le 4\)

Bình phương hai vế của (2) ta được:

\(\begin{array}{l} - {x^2} + 7x - 6 = {\left( {4 - x} \right)^2}\\ \Leftrightarrow  - {x^2} + 7x - 6 = 16 - 8x + {x^2}\\ \Leftrightarrow 2{x^2} - 15x + 22 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\left( {TM} \right)\\x = \frac{{11}}{2}\left( {KTM} \right)\end{array} \right.\end{array}\)

Vậy tập nghiệm của phương trình là \(S = \left\{ 2 \right\}\)

2:

\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)

\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)

B=(x1+x2)^2-2x1x2

=3^2-2*(-7)

=9+14=23

C=căn (x1+x2)^2-4x1x2

=căn 3^2-4*(-7)=căn 9+28=căn 27

D=(x1^2+x2^2)^2-2(x1x2)^2

=23^2-2*(-7)^2

=23^2-2*49=431

D=9x1x2+3(x1^2+x2^2)+x1x2

=10x1x2+3*23

=69+10*(-7)=-1

a) Tam thức \(f(x) =  - 5{x^2} + x - 1\) có \(\Delta  =  - 19 < 0\), hệ số \(a =  - 5 < 0\) nên f(x) luôn âm (cùng dấu với a) với mọi x, tức là \(\)\( - 5{x^2} + x - 1 < 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm

b) Tam thức \(g(x) = {x^2} - 8x + 16\) có \(\Delta  = 0\), hệ số a=1>0 nên g(x) luôn dương (cùng dấu với a) với mọi \(x \ne 4\), tức là \({x^2} - 8x + 16 > 0\) với mọi \(x \ne 4\)

Suy ra bất phương trình có nghiệm duy nhất là x = 4

c) Tam thức \(h(x) = {x^2} - x + 6\) có \(\Delta  =  - 23 < 0\), hệ số a=1>0 nên h(x) luôn dương (cùng dấu với a) với mọi x, tức là \({x^2} - x + 6 > 0\) với mọi \(x \in \mathbb{R}\). Suy ra bất phương trình có vô số nghiệm.

a \(\Leftrightarrow3x=12\Leftrightarrow x=4\)

b \(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{3}{2}\end{matrix}\right.\)

c \(ĐKXĐ:x\ne2;x\ne-2\)

\(\Rightarrow\left(x+2\right)^2-6\left(x-2\right)=x^2\Leftrightarrow x^2+4x+4-6x+12=x^2\Leftrightarrow-2x+16=0\Leftrightarrow-2x=-16\Leftrightarrow x=8\left(TM\right)\)

a) Ta có: 3x-12=0

\(\Leftrightarrow3x=12\)

hay x=4

Vậy: S={4}

b) Ta có: (x-2)(2x+3)=0

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\2x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-3}{2}\end{matrix}\right.\)

Vậy: \(S=\left\{2;\dfrac{-3}{2}\right\}\)

a) \(\sqrt {x + 2}  = x\)

Điều kiện: \(x \ge 0\)

Bình phương 2 vế của phương trình ta được:

\(x + 2 = {x^2} \Leftrightarrow {x^2} - x - 2 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 2\end{array} \right.\)

b) \(\sqrt {2{x^2} + 3x - 2}  = \sqrt {{x^2} + x + 6} \)

Bình phương 2 vế của phương trình ta được:

\(\begin{array}{l}2{x^2} + 3x - 2 = {x^2} + x + 6\\ \Leftrightarrow {x^2} + 2x - 8 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\x =  - 4\end{array} \right.\end{array}\)

Thay vào bất phương trình \(2{x^2} + 3x - 2 \ge 0\) ta thấy cả 2 nghiệm đều thỏa mãn.

Vậy tập nghiệm là \(S = \left\{ { - 4;2} \right\}\)

c) \(\sqrt {2{x^2} + 3x - 1}  = x + 3\)

Điều kiện: \(x + 3 \ge 0 \Leftrightarrow x \ge  - 3\)

Bình phương 2 vế của phương trình ta được:

\(\begin{array}{l}2{x^2} + 3x - 1 = {\left( {x + 3} \right)^2}\\ \Leftrightarrow {x^2} - 3x - 10 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 2\left( {tm} \right)\\x = 5\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy tập nghiệm là \(S = \left\{ { - 2;5} \right\}\)

a) \({\log _{\frac{1}{2}}}\left( {x - 2} \right) =  - 2\)

Điều kiện: \(x - 2 > 0 \Leftrightarrow x > 2\)

Vậy phương trình có nghiệm là \(x = 6\).

b) \({\log _2}\left( {x + 6} \right) = {\log _2}\left( {x + 1} \right) + 1\)

Điều kiện: \(\left\{ \begin{array}{l}x + 6 > 0\\x + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x >  - 6\\x >  - 1\end{array} \right. \Leftrightarrow x >  - 1\)

Vậy phương trình có nghiệm là \(x = 4\).

a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta  = 529 > 0\), có hai nghiệm phân biệt \({x_1} =  - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)

b) \( - 6{x^2} + 11x > 10 \Leftrightarrow  - 6{x^2} + 11x - 10 > 0\)

Xét tam thức \(f\left( x \right) =  - 6{x^2} + 11x - 10\) có \(\Delta  =  - 119 < 0\)và có \(a =  - 6 < 0\)

Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm

c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)

Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta  =  - 12 < 0\)và có \(a = 2 > 0\)

Ta có bảng xét dấu như sau

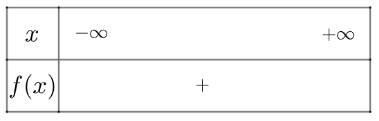
Vậy bất phương trình có vô số nghiệm

d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta  = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)