Tính đạo hàm của hàm số f x = x 2 + x + 1 k h i x < 1 x - 1 + 3 k h i x > 1
A. 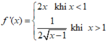
B. 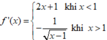
C. 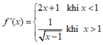
D. 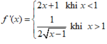
Biết hàm số f ( x ) - f ( 2 x ) có đạo hàm bằng 5 tại x = 1 và đạo hàm bằng 7 tại x = 2 Tính đạo hàm của hàm số f ( x ) - f ( 4 x ) tại x = 1.
A. 8.
B. 12.
C. 16.
D. 19.
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Trước hết ta xét: \(g\left(x\right)=\dfrac{1}{x+a}=\left(x+a\right)^{-1}\) với a là hằng số bất kì
\(g'\left(x\right)=-1.\left(x+a\right)^{-2}=\left(-1\right)^1.1!.\left(x+a\right)^{-\left(1+1\right)}\)
\(g''\left(x\right)=-1.\left(-2\right).\left(x+a\right)^{-3}=\left(-1\right)^2.2!.\left(x+a\right)^{-\left(2+1\right)}\)
Từ đó ta dễ dàng tổng quát được:
\(g^{\left(n\right)}\left(x\right)=\left(-1\right)^n.n!.\left(x+a\right)^{-\left(n+1\right)}=\dfrac{\left(-1\right)^n.n!}{\left(x+a\right)^{n+1}}\)
Xét: \(f\left(x\right)=\dfrac{x^2+1}{x\left(x-2\right)\left(x+2\right)}=-\dfrac{1}{4}.\left(\dfrac{1}{x}\right)+\dfrac{5}{8}\left(\dfrac{1}{x+2}\right)+\dfrac{5}{8}\left(\dfrac{1}{x-2}\right)\)
Áp dụng công thức trên ta được:
\(f^{\left(30\right)}\left(1\right)=\dfrac{1}{4}.\dfrac{\left(-1\right)^{30}.30!}{1^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1+2\right)^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1-2\right)^{31}}\)
Bạn tự rút gọn kết quả nhé
\(f\left(x\right)=\dfrac{x^2+1}{x^3}-4x\) hay \(f\left(x\right)=\dfrac{x^2+1}{x^3-4x}\) bạn?
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
Cho hàm số f(x), g(x) có đồ thị như hình vẽ. Đặt h ( x ) = f ( x ) g ( x ) . Tính h'(2) đạo hàm của hàm số h(x) tại x = 2.
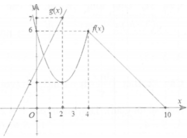
A. 4/49
B. -4/49
C. 2/7
D. -2/7
Cho hàm số \(f(x) = {2^{3x + 2}}\)
a) Hàm số f(x) là hàm hợp của hàm số nào?
b) Tìm đạo hàm của f(x)
a) Hàm số f(x) là hàm hợp của hàm số \(y = {a^x}\)
b) \(f'(x) = \left( {{2^{3x + 2}}} \right)' = \left( {3x + 2} \right)'{.2^{3x + 2}}.\ln 2 = {3.2^{3x + 2}}.\ln 2\)
Cho hàm số f(x), g(x) có đồ thị như hình vẽ. Đặt h x = f x g x . Tính h' (2) đạo hàm của hàm số h(x) tại x = 2.
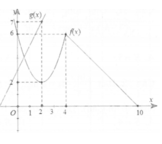
A. h ' 2 = 4 49
B. h ' 2 = - 4 49
C. h ' 2 = 2 7
D. h ' 2 = - 2 7
Tính đạo hàm của hàm số f(x)=ln x
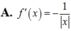
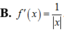
![]()
![]()
Tính đạo hàm f'(x) của hàm số f(x)= log 2 ( 3 x - 1 ) với x>1/
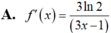

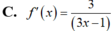
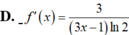
Tính đạo hàm của hàm số \(f\left( x \right)= \log x\) tại điểm \({x_0} = \frac{1}{2}\)
\(f'\left(x\right)=\dfrac{1}{x\cdot ln10}\)
=>\(f'\left(\dfrac{1}{2}\right)=\dfrac{1}{\dfrac{1}{2}\cdot ln10}=\dfrac{2}{ln10}\)