Cho hàm số y = x 4 - 2 ( 1 - m 2 ) x 2 + m + 1 . Tìm tất cả các giá trị của tham số thực m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất
A. m = - 1 2
B. m = 1 2
C. m = 0
D. m = 1
Những câu hỏi liên quan
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Đúng 0
Bình luận (0)
Bài 1: Xét tính đơn điệu của hàm số yf(x) khi biết đạo hàm của hàm số là:a) f(x)(x+1)(1-x^2)(2x-1)^3b) f(x)(x+2)(x-3)^2(x-4)^3Bài 2: Cho hàm số yf(x) có đạo hàm f(x)x(x+1)(x-2). Xét tính biến thiên của hàm số:a) yf(2-3x)b) yf(x^2+1)c) yf(3x+1)
Đọc tiếp
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
5 tháng 8 2023 lúc 9:58
Câu 25. Cho hàm số \(y = \dfrac{x + 1}{x - 1}, y = -x^3+x^2-3x+1, y = x^4 + 2x^2 +2.\) Trong các hàm số trên, có bao nhiêu hàm số đơn điệu trên \(R\)?
A. 1. B. 3. C. 0. D. 2.
\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
Đúng 2
Bình luận (1)
Bài 1 : Cho hàm số y=(m-3)x+4 . Với giá trị nào của m thì hàm số đồng biến, nghịch biến Bài 4: Cho hàm số y=(3-√2) x+1 a, Hàm số đồng biến hay nghịch biến? Vì sao? b, Tính các giá trị tương ứng của y khi x nhân các giá trị sau ; O, 1, √2, 3+√2, 3-√2
Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm
f
(
x
)
x
(
x
-
1
)
2
(
x
-
2
)
. Hỏi hàm số
y
f
5
x
x
2
+
4...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm f ' ( x ) = x ( x - 1 ) 2 ( x - 2 ) . Hỏi hàm số y = f 5 x x 2 + 4 đồng biến trên khoảng nào dưới đây ?
A. ( - ∞ ; - 2 ) .
B. (0;2).
C. (2;4).
D. (-2;1)
Cho hàm số
y
f
(
x
)
có đạo hàm
f
(
x
)
(
x
+
1
)...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) ( x - 2 ) 2 ( x - 3 ) 3 ( x + 5 ) 4 . Hỏi hàm số y = f ( x ) có mấy điểm cực trị?
A. 2
B. 3
C. 4
D. 5
Chọn A
f ' ( x ) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.
Đúng 0
Bình luận (0)
Cho các hàm số sau: \(y=\dfrac{1}{3}x^3-x^2+3x+4\); \(y=\sqrt{x^2+4}\);\(y=x^3+4x-sinx\);\(y=x^4+x^2+2\). Có bao nhiêu hàm số đồng biến trên những khoảng mà nó xác định
y'=1/3*3x^2-2x+3=x^2-2x+3=(x-1)^2+2>0
=>y=1/3x^3-x^2+3x+4 luôn đồng biến trên từng khoảng xác định
\(y=\sqrt{x^2+4}\)
=>\(y'=\dfrac{-\left(x^2+4\right)'}{\left(x^2+4\right)^2}=\dfrac{-\left(2x\right)}{\left(x^2+4\right)^2}\)
=>Hàm số này không đồng biến trên từng khoảng xác định
\(y=x^3+4x-sinx\)
=>y'=3x^2+4-cosx
-1<=-cosx<=1
=>3<=-cosx+4<=5
=>y'>0
=>Hàm số luôn đồng biến trên từng khoảng xác định
y=x^4+x^2+2
=>y'=4x^3+2x=2x(2x^2+1)
=>Hàm số ko đồng biến trên từng khoảng xác định
Đúng 1
Bình luận (0)
Cho hàm số yf(x) có đồ thị đạo hàm yf’(x) được cho như hình vẽ bên và các mệnh đề sau:(1). Hàm số yf(x) có duy nhất 1 điểm cực trị(2). Hàm số yf(x) nghịch biến trên khoảng (-2;1) (3). Hàm số yf(x) đồng biến trên khoảng
0
;
+
∞
(4). Hàm số
g
x
f
x
+
x
2
có 2 điểm cực trị.Số mệnh đề đúng...
Đọc tiếp
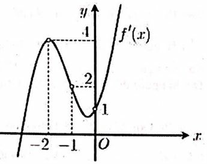
Cho hàm số y=f(x) có đồ thị đạo hàm y=f’(x) được cho như hình vẽ bên và các mệnh đề sau:
(1). Hàm số y=f(x) có duy nhất 1 điểm cực trị
(2). Hàm số y=f(x) nghịch biến trên khoảng (-2;1)
(3). Hàm số y=f(x) đồng biến trên khoảng 0 ; + ∞
(4). Hàm số g x = f x + x 2 có 2 điểm cực trị.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho các hàm số dưới đây, có bao nhiêu hàm số là hàm số chẵn:
y
cos
3
x
(
1
)
;
y
sin
(
x
2
+
1
)
(
2
)
;
y
tan
2
x
(
3
)...
Đọc tiếp
Cho các hàm số dưới đây, có bao nhiêu hàm số là hàm số chẵn:
y = cos 3 x ( 1 ) ; y = sin ( x 2 + 1 ) ( 2 ) ; y = tan 2 x ( 3 ) ; y = c o t x ( 4 )
A.1
B. 2
C. 3
D. 4
+ Xét hàm số y= f(x) = cos3x
TXĐ: D =R
Với mọi x ∈ D , ta có: - x ∈ D và
f( -x) = cos( - 3x) = cos3x = f(x)
Do đó, y= cos 3x là hàm chẵn trên tập xác định của nó.
+ Xét hàm y= g(x)= sin(x2 + 1)
TXĐ: D= R
Với mọi x ∈ D , ta có: - x ∈ D và
g( -x)= sin[ (-x)2 +1]= sin( x2+1)= g(x)
Do đó: y= sin( x2 +1) là hàm chẵn trên R.
+ Xét hàm số y= h( x)= tan2x .
TXĐ: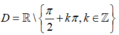 
Với mọi x ∈ D , ta có: - x ∈ D và
h( -x)= tan2 (-x)= (- tanx)2 = tan2 x= h(x)
Do đó y= tan2x là hàm số chẵn trên D.
+ Xét hàm số y= t(x)= cotx.
TXĐ: 
Với mọi x ∈ D , ta có: - x ∈ D và t(-x)= cot(-x) = - cotx = - t(x)
Do đó: y= cotx là hàm số lẻ trên D.
Vậy (1); (2); (3) là các hàm số chẵn
Đáp án C
Đúng 0
Bình luận (0)
phần 1
-hệ phương trình
/
| 3 x - 4 y 7
| 2 x + Sy -1
-hàm số và đồ thị của hàm số y a x²
Đồng biến nghịch biến tìm hệ số a
vd : cho hàm số y ax² (P)
a, tìm a cho biết đồ thị hàm số đi qua A ( -3 ; 3 )
b, vẽ đồ thị hàm số với a vừa tìm được
- giải bài toán bằng hệ phương trình
- chứng minh tứ giác nội tiếp ( các điểm cùng thuộc 1 đường tròn )
- các góc bằng nhau . L là góc nội tiếp
- chứng minh bất đẳng thức
phương trình bặc nhất 2 ẩn ; nghiệ...
Đọc tiếp
phần 1 -hệ phương trình / | 3 x - 4 y = 7 < | 2 x + Sy = -1 \ -hàm số và đồ thị của hàm số y = a x² Đồng biến nghịch biến tìm hệ số a vd : cho hàm số y = ax² (P) a, tìm a cho biết đồ thị hàm số đi qua A ( -3 ; 3 ) b, vẽ đồ thị hàm số với a vừa tìm được - giải bài toán bằng hệ phương trình - chứng minh tứ giác nội tiếp ( các điểm cùng thuộc 1 đường tròn ) - các góc bằng nhau . L là góc nội tiếp - chứng minh bất đẳng thức phương trình bặc nhất 2 ẩn ; nghiệm của phương trình a x + b y = c ( Xo ; Yo ) 2 hệ tương đương khi có cùng tập nghiệm hàm số đồng biến , nghịch biến và tìm hệ số điểm thuộc đồ thị vị trí tương đối của 2 đường tròn , đường tròn ngoại tiếp của tam giác tính chất 2 tiếp tuyến cắt nhau tứ giác nối tiếp - công thức nghiệm tam giác - một mảnh vườn hình chữ nhật có nhiều dài lớn hơn chiều rộng 6m ; mảnh vườn là 160 m² tìm cách kích thước của mảnh vườn
3:
Gọi chiều rộng là x
=>Chiềudài là x+6
Theo đề, ta có: x(x+6)=160
=>x^2+6x-160=0
=>(x+16)(x-10)=0
=>x-10=0
=>x=10
=>Chiều dài là 16m
Đúng 1
Bình luận (0)