\(\sqrt{\left(x-1\right)^2}=\left|x-1\right|\)

Chọn C

ChọnC

C.

ĐKXĐ: x≥0

Ta có: (\(\sqrt{5+\sqrt{x}}\))\(^2\)= 4\(^2\) ⇔ l\(5+\sqrt{x}\)l = 16

TH1) \(5+\sqrt{x}=16\)⇔\(\sqrt{x}\)= 11⇔x = 121 (TM)

TH2) 5+\(\sqrt{x}\) = -16⇔ \(\sqrt{x}\) = -21(vô nghiệm)

Vậy x = 121=> Chọn C

a: \(x^2-4x-5=\left(x-5\right)\left(x+1\right)\)

b: \(x^2-3x+2=\left(x-2\right)\left(x-1\right)\)

d: \(2x^2-3x+1=\left(x-1\right)\left(2x-1\right)\)

k: \(4x^2-9=\left(2x-3\right)\left(2x+3\right)\)

Chọn A

A

A

a. \(R=\dfrac{R1.R2}{R1+R2}=\dfrac{10.15}{10+15}=6\Omega\)

b + c. \(U=U1=U2=IR=1,5.6=9V\)(R1//R2)

\(\left\{{}\begin{matrix}I1=U1:R1=9:10=0,9A\\I2=U2:R2=9:15=0,6A\end{matrix}\right.\)

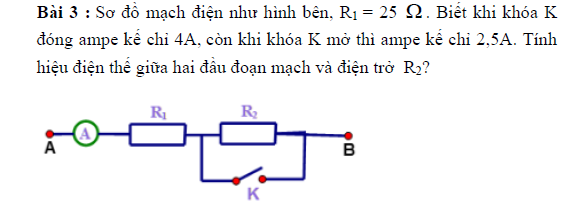
Ta có: Khi khóa K đóng thì dòng điện sẽ không đi qua R₂ nên số chỉ của Ampe kế là số chỉ của cường độ dòng điện chạy trong mạch, tức là khi khóa K đóng: 4A.

Hiệu điện thế giữa hai đầu đoạn mạch:

\(U=IR1=4.25=100V\)

Khi khóa K mở thì R1 nt R2, nên sẽ có cường độ dòng điện đi qua mạch, tức là cường độ dòng điện khi khóa K mở: 4A.

Điện trở tương đương: \(R=U:I=100:2,5=40\Omega\)

\(\Rightarrow R2=R-R1=40-25=15\Omega\)

Bài `4`

`1, 2y(x+2)-3x-6`

`=2y(x+2) -(3x+6)`

`=2y(x+2) -3(x+2)`

`=(x+2)(2y-3)`

`2, 3(x+4) -x^2-4x`

`=3(x+4)-(x^2+4x)`

`=3(x+4) -x(x+4)`

`=(x+3)(3-x)`

`3, 2(x+5) -x^2-5x`

`=2(x+5)-(x^2+5x)`

`=2(x+5)-x(x+5)`

`=(x+5)(2-x)`

`4, x^2 +6x-3(x+6)`

`= (x^2+6x) -3(x+6)`

`=x(x+6)-3(x+6)`

`=(x+6)(x-3)`

`5, x(x+y) -5x-5y`

`=x(x+y) -(5x+5y)`

`=x(x+y)-5(x+y)`

`=(x+y)(x-5)`

`6,x(x-y)+2x-2y`

`=x(x-y)+2(x-y)`

`=(x-y)(x+2`

Bạn tách ra từng bài đi ạ. Làm all trong 1 câu nhiều lắm.

Em ko muốn bài giải vậy Thầy xóa đây. Em tự xem lại cách học của mình nhé!

ĐKXĐ: \(\left\{{}\begin{matrix}-3x\ge0\\x^2-1\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le0\\x^2\ne1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\le0\\x\ne\pm1\end{matrix}\right.\)

\(\sqrt{2x+5}\) xác định khi \(2x+5\ge0\Rightarrow2x\ge-5\Rightarrow x\ge-\dfrac{5}{2}\)

\(\sqrt{2x+5}\le0\Leftrightarrow2x+5\le0\Leftrightarrow2x\le-5\Leftrightarrow x\ge\dfrac{-5}{2}\)

\(\Rightarrow\) Đáp án:   A

Chọn A