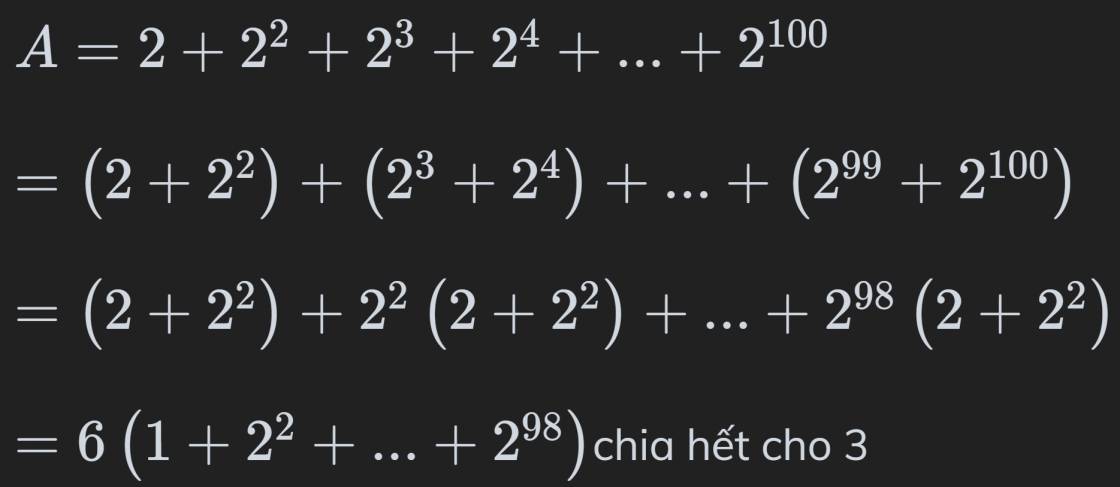Chứng tỏ:A=31+32+33+...+360 chia hết cho 13

Những câu hỏi liên quan
14. Cho B = 3 + 32 + 33 + …. + 360. Chứng tỏ rằng:
a) B chia hết cho 4;
b) B chia hết cho 13.
a) B\(=\) 3 + 32 + 33 + ... + 360
\(=\)(3+32)+(33+34)+...+(359+360)
\(=\)3(1+3)+33(1+3)+...+359(1+3)
\(=\)(3+1)(3+33+...+359)
\(=\)4(3+33+...+359)⋮4
⇒B⋮4
b) B\(=\)(3+32+33)+...+(358+359+360)
\(=\)30(3+32+33)+...+357(358+359+360)
\(=\)3+32+33(30+33+36+...+357)
\(=\)39(30+33+36+...+357)⋮13
⇒ B⋮13
Đúng 1
Bình luận (0)
a)Chứng tỏ: A = 31 + 32 + 33 + … + 360 chia hết cho 13
b)Cho M = 2 + 22 + 23 + … + 220 . Chứng tỏ rằng M
![]()
5
đăng 3 lần rồi giúp mik ik
\(A=\left(3+3^2+3^3\right)+...+\left(3^{58}+3^{59}+3^{60}\right)\\ A=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\\ A=\left(1+3+3^2\right)\left(3+...+3^{58}\right)\\ A=13\left(3+...+3^{58}\right)⋮13\)
\(M=\left(2+2^2+2^3+2^4\right)+...+\left(2^{17}+2^{18}+2^{19}+2^{20}\right)\\ M=\left(2+2^2+2^3+2^4\right)+...+2^{16}\left(2+2^2+2^3+2^4\right)\\ M=\left(2+2^2+2^3+2^4\right)\left(1+...+2^{16}\right)\\ M=30\left(1+...+2^{16}\right)⋮5\)
Đúng 6
Bình luận (0)
a)Chứng tỏ: A = 31 + 32 + 33 + … + 360 chia hết cho 13
b)Cho M = 2 + 22 + 23 + … + 220 . Chứng tỏ rằng M ![]() 5
5
hãy giúp mik ik mik cần gắp
a)Chứng tỏ: A = 31 + 32 + 33 + … + 360 chia hết cho 13
b)Cho M = 2 + 22 + 23 + … + 220 . Chứng tỏ rằng M ![]() 5
5
hãy giúp mik và chỉ cách trình bày cho mik nhen
Bài 5. Cho B = 30 + 31 + 32 + 33 + .... + 3100. Chứng tỏ B chia hết cho 13
\(B=3^0+3^1+3^2...+3^{100}\)
\(=3^0\times\left(1+3^1+3^2\right)+3^3\times\left(1+3^1+3^2\right)+...+3^{98}\times\left(1+3^1+3^2\right)\)
\(=3^0\times13+3^3\times13+...+3^{98}\times13\)
\(=13\times\left(3^0+3^3+...+3^{98}\right)⋮13\)
Đúng 1
Bình luận (0)
Chứng minh : 3 + 32 + 33+ .....+ 360 chia hết cho 13
Làm ơn giúp mình trong tối nay
a. Chứng minh A=21+22+23+24+...+2100 chia hết cho 3
b. Chứng minh B=31+32+33+34+...+299chia hết cho 13
c. Chứng minh C=51+52+53+54+...+5105 chia hết cho 6 và 31
a) Chứng minh: A = 21 +22 +23 +24 +...+ 22020 chia hết cho 3; và 7.
b) Chứng minh: B =31 +32 +33 +34 +...+22022 chia hết cho 4 và 13.
Câu 1:
$A=(2+2^2)+(2^3+2^4)+(2^5+2^6)+....+(2^{2019}+2^{2020})$
$=2(1+2)+2^3(1+2)+2^5(1+2)+....+2^{2019}(1+2)$
$=(1+2)(2+2^3+2^5+...+2^{2019})=3(2+2^3+2^5+...+2^{2019})\vdots 3$
-----------------
$A=2+(2^2+2^3+2^4)+(2^5+2^6+2^7)+....+(2^{2018}+2^{2019}+2^{2020})$
$=2+2^2(1+2+2^2)+2^5(1+2+2^2)+....+2^{2018}(1+2+2^2)$
$=2+(1+2+2^2)(2^2+2^5+....+2^{2018})$
$=2+7(2^2+2^5+...+2^{2018})$
$\Rightarrow A$ chia $7$ dư $2$.
Đúng 0
Bình luận (0)
Câu 2:
$B=(3+3^2)+(3^3+3^4)+....+(3^{2021}+3^{2022})$
$=3(1+3)+3^3(1+3)+...+3^{2021}(1+3)$
$=(1+3)(3+3^3+...+3^{2021})=4(3+3^3+....+3^{2021})\vdots 4$
-------------------
$B=(3+3^2+3^3)+(3^4+3^5+3^6)+...+(3^{2020}+3^{2021}+3^{2022})$
$=3(1+3+3^2)+3^4(1+3+3^2)+....+3^{2020}(1+3+3^2)$
$=(1+3+3^2)(3+3^4+...+3^{2020})=13(3+3^4+...+3^{2020})\vdots 13$ (đpcm)
Đúng 1
Bình luận (0)
Cho B = 3 + 32 + 33 + …… + 360. Hãy cho biết B có chia hết cho 13 không? Vì sao?
\(B=3+3^2+3^3+...+3^{60}\)
\(=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{58}\right)⋮13\)
Đúng 2
Bình luận (0)