Cho hàm số y=f(x) có đạo hàm liên tục trên tập R/ 2 và có đồ thị hàm số y=f’(x) như hình vẽ. Biết f 1 ≠ 10 f(3)=4 . Có bao nhiêu tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó song song với đường thẳng 3x+y-13
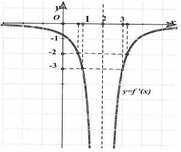
A. 2
B. 1
C. 0.
D. 3
Cho hàm số \(y=x^4-2x^2\) có đồ thị (C) . Hỏi có bao nhiêu tiếp tuyến của đồ thị (C) song song với trục hoành ?
Lời giải:
Để PTTT tại $x=x_0$ song song với trục hoành thì $f'(x_0)=0$ và $f(x_0)\neq 0$
$f'(x)=4x^3-4x=0\Leftrightarrow x=0;1;-1$
Thử các giá trị $x$ này vô $f(x_0)$ xem có khác $0$ hay không ta thu được $x=\pm 1$
Tức là có 2 tiếp tuyến của $(C)$ song song với trục hoành.
Cho hàm số y = - x 3 + 2 x 2 có đồ thị (C). Có bao nhiêu tiếp tuyến của đồ thị (C) song song với đường thẳng y=x
A. 2
B. 3
C. 1
D. 4
Cho hàm số y = x - 2/x + 3 có đồ thị C sao cho điểm M trên đồ thị c tiếp tuyến của C tại M tạo với hai trục tọa độ một tam giác có diện tích bằng 18/5
Bài 4: Cho hàm số y = - x ^ 3 + 3x ^ 2 + 9x + 5 (C). Trong tất cả các tiếp tuyến của đồ thị (C), hãy tìm tiếp tuyến có hệ số góc lớn nhất.
Ta có y’ = -3x2 – 6x + 9
Gọi xo là hoành độ tiếp điểm của tiếp tuyến, ta có f’(xo) = -3xo2 – 6xo + 9
⇔ f’(xo) = -3(xo2 + 2xo + 1) + 12 = -3(xo + 1)2 + 12 ≤ 12
Từ đó suy ra maxf’(xo) = 12 tại xo = -1.
Với xo = -1 ⇒ yo = -16, phương trình tiếp tuyến cần tìm: y = 12x - 4.
Chúc bn học tốt
1/Viết pt tiếp tuyến của đồ thị hàm số y=\(\frac{2x}{x-2}\) Tại điểm có hoành độ bằng 3
2/có bao nhiêu tiếp tuyến với đồ thị hàm số: y=\(\frac{2x+3}{x-1}\) biết tiếp tuyến song song với đường thẳng y=-5x-3
a/
\(y'=-\frac{4}{\left(x-2\right)^2}\Rightarrow\left\{{}\begin{matrix}y'\left(3\right)=-4\\y\left(3\right)=6\end{matrix}\right.\)
Pt tiếp tuyến: \(y=-4\left(x-3\right)+6\Leftrightarrow y=-4x+18\)
b.
\(y'=\frac{-5}{\left(x-1\right)^2}\)
Tiếp tuyến song song với \(y=-5x-3\) nên có hệ số góc \(k=-5\)
\(\Rightarrow\frac{-5}{\left(x-1\right)^2}=-5\Rightarrow\left(x-1\right)^2=1\Rightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
Có 2 tiếp tuyến thỏa mãn
a) tìm hệ số góc của tiếp tuyến của đồ thị hàm số y=-x^3+3x-2 (c) tại điểm có hoành độ -3
b) viết phương trình tiếp tuyến của đồ thị hàm số (c) trên tại điểm ( ứng với tiếp điểm ) có hoành độ -3
1//Cho hàm số y=x3- 2x2+ 2x có đồ thị (C). Gọi x1,x2 là hoành độ các điểm M,N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y=-x+2017. Khi đó x1+x2 bằng bao nhiêu?
2// Hoành độ tiếp điểm của tiếp tuyến song song với trục hoành của đồ thị hàm số y=x3-3x+2
3// Tiếp tuyến của đồ thị y=\(\frac{x^3}{3}+3x^2-2\) Có hệ số góc k=-9 , có phương trình là gì
4//Cho hs \(y=-x^3+3x^3-3\) có đồ thị (C) Số tiếp tuyến (C) vuông góc với đường thẳng \(y=\frac{1}{9}x+2017\)
1.
Tiếp tuyến vuông góc với \(y=-x+2017\) nên có hệ số góc \(k=\frac{-1}{-1}=1\)
\(y'=3x^2-4x+2=1\)
\(\Rightarrow3x^2-4x+1=0\Rightarrow\left[{}\begin{matrix}x=1\\x=\frac{1}{3}\end{matrix}\right.\)
\(\Rightarrow x_1+x_2=1+\frac{1}{3}=\frac{4}{3}\)
2.
Tiếp tuyến song song Ox nên có hệ số góc \(k=0\)
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
3.
\(y'=x^2+6x=-9\Rightarrow\left(x+3\right)^2=0\Rightarrow x=-3\Rightarrow y=16\)
Pt tiếp tuyến: \(y=-9\left(x+3\right)+16=-9x-11\)
4.
Tiếp tuyến vuông góc \(y=\frac{1}{9}x+2017\) có hệ số góc \(k=\frac{-1}{\frac{1}{9}}=-9\)
\(y'=-3x^2+6x=-9\Leftrightarrow3x^2-6x-9=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
Có 2 tiếp điểm nên có 2 tiếp tuyến thỏa mãn
Cho hàm số y = x - 1 2 x + 2 có đồ thị (C). Có bao nhiêu tiếp tuyến của (C) tạo với hai trục tọa một tam giác có trọng tâm nằm trên đường thẳng y = - x
A. 4.
B. 1.
C. 3.
D. 2.
Cho hàm số y = x - 1 2 x + 2 có đồ thị (C). Có bao nhiêu tiếp tuyến của (C) tạo với hai trục tọa một tam giác có trọng tâm nằm trên đường thẳng y=-x.
A. 4.
B. 1.
C. 3.
D. 2.
