Tính tích phân ∫ 0 2 max x , x 3 d x .
A. 2
B. 4
C. 15 4
D. 17 4
Những câu hỏi liên quan
f(x)^3 + f(x)= x Tính tích phân f(x)dx từ 0 đến 2
Cho hàm số y f(x) liên tục trên đoạn [0;1] thoả mãn
∫
0
1
x
2
f
(
x
)
d
x
0
và
m
a
x
[
0
;
1
]
f
(...
Đọc tiếp
Cho hàm số y = f(x) liên tục trên đoạn [0;1] thoả mãn ∫ 0 1 x 2 f ( x ) d x = 0 và m a x [ 0 ; 1 ] f ( x ) = 6 Giá trị lớn nhất của tích phân ∫ 0 1 x 3 f ( x ) d x bằng
Cho hàm số y f(x) liên tục trên [0;1] thỏa mãn
∫
0
1
x
f
(
x
)
d
x
0
và
m
a
x
[
0
;
1
]
f
(...
Đọc tiếp
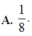
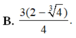
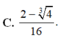
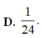
Cho hàm số y = f(x) liên tục trên [0;1] thỏa mãn ∫ 0 1 x f ( x ) d x = 0 và m a x [ 0 ; 1 ] f ( x ) = 1 Tích phân I = ∫ 0 1 e x f ( x ) d x thuộc khoảng nào trong các khoảng sau đây?
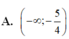
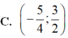
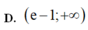
phân tích đa thức thành nhân tử 2x(x-y)-3x+3y
thực hiện phép tính (x-9/x^2-9)-(3/x^2+3x)
chứng tỏ rằng 2x-x^2-0<0 với mọi giá trị của x
\(2x\left(x-y\right)-3x+3y=2x\left(x-y\right)-\left(3x-3y\right)=2x\left(x-y\right)-3\left(x-y\right)=\left(x-y\right)\left(2x-3\right)\)
Đúng 1
Bình luận (0)
Bài1: Thực hiện phép tính a) 2x(3x2 – 5x + 3) b) - 2x ( x2 + 5x+3) Bài 4: Tìm x, biết.a/ 3x + 2(5 – x) 0 b/ x(2x – 1)(x + 5) – (2x2 + 1)(x + 4,5) 3,5c/ 3x2 – 3x(x – 2) 36.II. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ Bài1: Phân tích đa thức thành nhân tử.a/ 14x2y – 21xy2 + 28x2y2 b/ x(x + y) – 5x – 5y.c/ 10x(x – y) – 8(y – x). d/ (3x + 1)2 – (x + 1)2e/ 5x2 – 10xy + 5y2 – 20z2. f/ x2 + 7x – 8g/ x3 – x + 3x2y + 3xy2 + y3 – y h/ x2 + 4x + 3.
Đọc tiếp
Bài1: Thực hiện phép tính
a) 2x(3x2 – 5x + 3) b) - 2x ( x2 + 5x+3)
Bài 4: Tìm x, biết.
a/ 3x + 2(5 – x) = 0 b/ x(2x – 1)(x + 5) – (2x2 + 1)(x + 4,5) = 3,5
c/ 3x2 – 3x(x – 2) = 36.
II. PHÂN TÍCH ĐA THỨC THÀNH NHÂN TỬ
Bài1: Phân tích đa thức thành nhân tử.
a/ 14x2y – 21xy2 + 28x2y2 b/ x(x + y) – 5x – 5y.
c/ 10x(x – y) – 8(y – x). d/ (3x + 1)2 – (x + 1)2
e/ 5x2 – 10xy + 5y2 – 20z2. f/ x2 + 7x – 8
g/ x3 – x + 3x2y + 3xy2 + y3 – y h/ x2 + 4x + 3.
Bài 1:
a: \(=6x^3-10x^2+6x\)
b: \(=-2x^3-10x^2-6x\)
Bài 4:
a: =>3x+10-2x=0
=>x=-10
c: =>3x2-3x2+6x=36
=>6x=36
hay x=6
Đúng 0
Bình luận (0)
Bài 1:
\(a,=6x^3-10x^2+6x\\ b,=-2x^3-10x^2-6x\)
Bài 4:
\(a,\Leftrightarrow3x+10-2x=0\Leftrightarrow x=-10\\ b,\Leftrightarrow x\left(2x^2+9x-5\right)-\left(2x^3+9x^2+x+4,5\right)=3,5\\ \Leftrightarrow2x^3+9x^2-5x-2x^3-9x^2-x-4,5=3,5\\ \Leftrightarrow-6x=8\Leftrightarrow x=-\dfrac{4}{3}\\ c,\Leftrightarrow3x^2-3x^2+6x=36\Leftrightarrow x=6\)
Bài 1:
\(a,=7xy\left(2x-3y+4xy\right)\\ b,=x\left(x+y\right)-5\left(x+y\right)=\left(x-5\right)\left(x+y\right)\\ c,=\left(x-y\right)\left(10x+8\right)=2\left(5x+4\right)\left(x-y\right)\\ d,=\left(3x+1-x-1\right)\left(3x+1+x+1\right)\\ =2x\left(4x+2\right)=4x\left(2x+1\right)\\ e,=5\left[\left(x-y\right)^2-4z^2\right]=5\left(x-y-2z\right)\left(x-y+2z\right)\\ f,=x^2+8x-x-8=\left(x+8\right)\left(x-1\right)\\ g,\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\\ h,=x^2+3x+x+3=\left(x+3\right)\left(x+1\right)\)
Đúng 1
Bình luận (0)
cho x≠0, y≠0 thỏa mãn: (x+y)xy=x2+y2-xy. Tính max A=\(\dfrac{1}{x^3}+\dfrac{1}{y^3}\)
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y}\). khi đó gt trở thành:
\(a+b=a^2+b^2-ab\ge\dfrac{1}{4}\left(a+b\right)^2\Leftrightarrow o\le a+b\le4\);
\(A=a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)=\left(a+b\right)^2\le16\)
Đẳng thức xảy ra khi và chỉ khi a=b=2 <=> x=y=1/2
Vậy Max A = 16
Đúng 1
Bình luận (0)
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) 0, F(2) 1, G(2) 1 và
∫
0
2
F
(
x
)
g
(
x
)
d
x
3 . Tính tích phân hàm:
∫
0
2
G
(
x
)
f
(
x
)
d
x
A. I 3. B. I 0....
Đọc tiếp
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.
Đúng 0
Bình luận (0)
cho \(y=ax^2+bx+c=f\left(x\right)\) có đồ thị đi qua \(A\left(1;8\right),Max=9\) tại x=2
tìm m để
a, \(3\left|f\left(x\right)\right|+m-5=0\) có 3 nghiệm phân biệt
b,\(2f\left(\left|x\right|\right)-7+5m=0\) có 4 nghiệm pb
Từ điều kiện đề bài \(\Rightarrow\left\{{}\begin{matrix}a+b+c=8\\-\dfrac{b}{2a}=2\\\dfrac{4ac-b^2}{4a}=9\end{matrix}\right.\Rightarrow f\left(x\right)=-x^2+4x+5\)
a. Không tồn tại m để \(3\left|f\left(x\right)\right|+m-5=0\) có 3 nghiệm phân biệt (nếu pt đã cho có 3 nghiệm thì 1 nghiệm trong đó luôn là nghiệm kép). Có 3 nghiệm thì được (khi đó \(\dfrac{5-m}{3}=9\Rightarrow m\))
b. \(2f\left(\left|x\right|\right)-7+5m=0\Leftrightarrow f\left(\left|x\right|\right)=\dfrac{-5m+7}{2}\) (1)
Đồ thì hàm \(y=f\left(\left|x\right|\right)\) (tạo ra bằng cách bỏ phần bên trái trục Oy và lấy đối xứng phần bên phải của đồ thị \(y=f\left(x\right)\) qua):
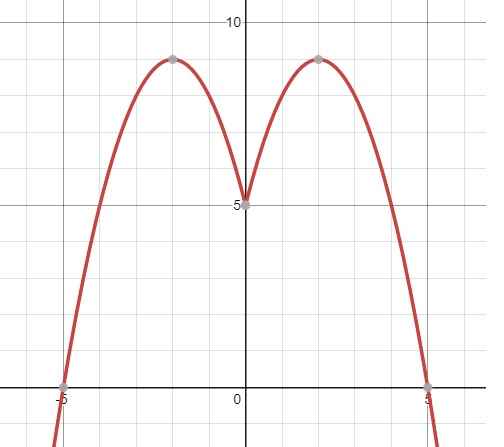
Từ đồ thị ta thấy (1) có 4 nghiệm pb khi:
\(5< \dfrac{-5m+7}{2}< 9\) \(\Rightarrow-\dfrac{11}{5}< m< -\dfrac{3}{5}\)
Đúng 1
Bình luận (0)
phân tích thành nhân tử
\(A=x^3+y^3+z^3-3xyz\)
từ đó tìm nghiệm nguyên (x, y, z) của phương trình
\(x^3+y^3+z^3-3xyz=x\left(y-z\right)^2+z\left(x-y\right)^2+y\left(z-x\right)^2\)
thỏa mãn điều kiện
\(max\left(x,y,z\right)< x+y+z-max\left(x,y,z\right)\)
Cho phương trình x^2 + 2(m - 3)x + m^2 =0 a. Giải phương trình với m = 0 b. Tìm m pt có hai nghiệm phân biệt. Tính tổng và tích hai nghiệm theo m
a. Bạn tự giải
b.
Pt có 2 nghiệm phân biệt khi:
\(\Delta'=\left(m-3\right)^2-m^2>0\)
\(\Leftrightarrow-6m+9>0\)
\(\Leftrightarrow m< \dfrac{3}{2}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-3\right)\\x_1x_2=m^2\end{matrix}\right.\)
Đúng 0
Bình luận (0)