Từ điều kiện đề bài \(\Rightarrow\left\{{}\begin{matrix}a+b+c=8\\-\dfrac{b}{2a}=2\\\dfrac{4ac-b^2}{4a}=9\end{matrix}\right.\Rightarrow f\left(x\right)=-x^2+4x+5\)
a. Không tồn tại m để \(3\left|f\left(x\right)\right|+m-5=0\) có 3 nghiệm phân biệt (nếu pt đã cho có 3 nghiệm thì 1 nghiệm trong đó luôn là nghiệm kép). Có 3 nghiệm thì được (khi đó \(\dfrac{5-m}{3}=9\Rightarrow m\))
b. \(2f\left(\left|x\right|\right)-7+5m=0\Leftrightarrow f\left(\left|x\right|\right)=\dfrac{-5m+7}{2}\) (1)
Đồ thì hàm \(y=f\left(\left|x\right|\right)\) (tạo ra bằng cách bỏ phần bên trái trục Oy và lấy đối xứng phần bên phải của đồ thị \(y=f\left(x\right)\) qua):
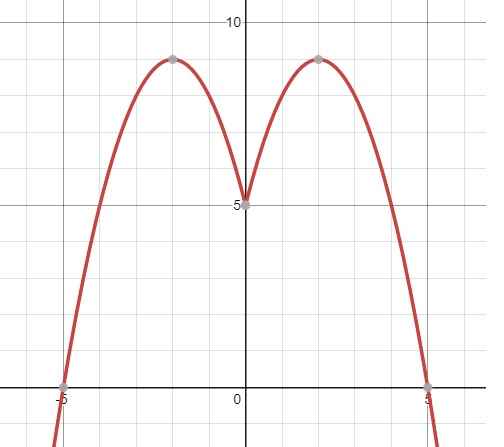
Từ đồ thị ta thấy (1) có 4 nghiệm pb khi:
\(5< \dfrac{-5m+7}{2}< 9\) \(\Rightarrow-\dfrac{11}{5}< m< -\dfrac{3}{5}\)





