Ôn tập chương I
Nội dung lý thuyết
I. CÁC ĐỊNH NGHĨA
1. Định nghĩa vectơ
- Định nghĩa: Vectơ là một đoạn thẳng có hướng.
- Vectơ có điểm đầu \(A\), điểm cuối \(B\) được kí hiệu là \(\overrightarrow{AB}\) và đọc là "vectơ \(AB\)". Để vẽ vectơ \(\overrightarrow{AB}\) ta vẽ đoạn thẳng \(AB\) và đánh dấu mũi tên ở đầu mút \(B\).
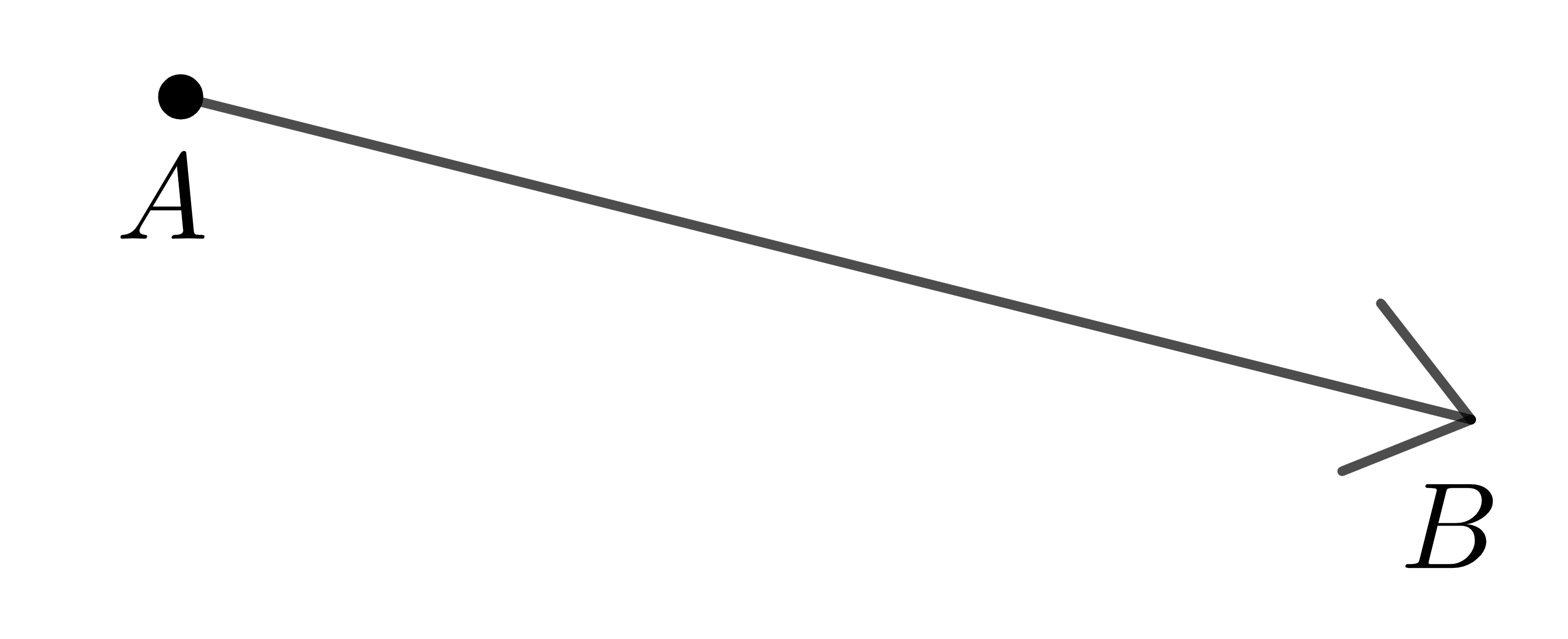
Ngoài ra vectơ có thể được kí hiệu là \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{x},\overrightarrow{y}\)... khi không cần chỉ rõ điểm đầu và điểm cuối của nó.

2. Hai vectơ cùng phương
- Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Trong các vectơ trên, vectơ \(\overrightarrow{AB}\) và vectơ \(\overrightarrow{CD}\) là hai vectơ cùng phương và cùng có chiều đi từ trái sang phải. Ta nói \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\) là hai vectơ cùng hướng.
Tương tự, vectơ \(\overrightarrow{PQ}\) và vectơ \(\overrightarrow{RS}\) cùng phương nhưng có hướng ngược nhau. Ta nói \(\overrightarrow{PQ}\) và \(\overrightarrow{RS}\) là hai vectơ ngược hướng.
- Nhận xét: Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng phương.
3. Hai vectơ bằng nhau
- Mỗi vectơ có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của vectơ \(\overrightarrow{AB}\) được kí hiệu là \(\left|\overrightarrow{AB}\right|\), như vậy \(\left|\overrightarrow{AB}\right|=AB\).
Vectơ có độ dài bằng 1 gọi là vectơ đơn vị.
Hai vectơ \(\overrightarrow{a},\overrightarrow{b}\) được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu \(\overrightarrow{a}=\overrightarrow{b}\)
- Chú ý: Khi cho trước vectơ \(\overrightarrow{a}\) và điểm \(O\) thì ta luôn tìm được một điểm \(A\) duy nhất sao cho \(\overrightarrow{OA}=\overrightarrow{a}\).
4. Vectơ - không
- Vectơ - không là vectơ có điểm đầu và điểm cuối trùng nhau.
Ví dụ: \(\overrightarrow{AA}\) là một vectơ - không.
- Vectơ - không cùng phương, cùng hướng với mọi vectơ.
- Quy ước độ dài của vectơ - không bằng 0.
Ví dụ: \(\left|\overrightarrow{AA}\right|=0\).
- Ta kí hiệu vectơ - không là \(\overrightarrow{0}\). Như vậy \(\overrightarrow{0}=\overrightarrow{AA}=\overrightarrow{BB}=...\)
@1950063@
II. TỔNG VÀ HIỆU CỦA HAI VECTƠ
1. Tổng của hai vectơ
- Định nghĩa: Cho hai vectơ \(\overrightarrow{a},\overrightarrow{b}\). Lấy một điểm \(A\) tuỳ ý, vẽ \(\overrightarrow{AB}=\overrightarrow{a}\), \(\overrightarrow{BC}=\overrightarrow{b}\). Khi đó vectơ \(\overrightarrow{AC}\) được gọi là tổng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\). Ta kí hiệu tổng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là \(\overrightarrow{a}+\overrightarrow{b}\). Vậy \(\overrightarrow{AC}=\overrightarrow{a}+\overrightarrow{b}\).

2. Quy tắc hình bình hành
Nếu \(ABCD\) là hình bình hành thì \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\).

3. Tính chất của phép cộng các vectơ
Với ba vectơ \(\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}\) tuỳ ý ta có:
\(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\) (tính chất giao hoán) ;
\(\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)\) (tính chất kết hợp) ;
\(\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}\) (tính chất cộng với vectơ - không).

4. Hiệu của hai vectơ
- Vectơ đối của vectơ \(\overrightarrow{a}\) là một vectơ có cùng độ dài và ngược hướng với \(\overrightarrow{a}\), kí hiệu là \(-\overrightarrow{a}\).
Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của \(\overrightarrow{AB}\) là \(\overrightarrow{BA}\), nghĩa là \(-\overrightarrow{AB}=\overrightarrow{BA}\).
Vectơ đối của vectơ \(\overrightarrow{0}\) là vectơ \(\overrightarrow{0}\).
- Cho hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\). Ta gọi hiệu của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là vectơ \(\overrightarrow{a}+\left(-\overrightarrow{b}\right)\), kí hiệu \(\overrightarrow{a}-\overrightarrow{b}\)
Như vậy: \(\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+\left(-\overrightarrow{b}\right)\)
- Với ba điểm \(O,A,B\) tuỳ ý ta có \(\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\).

- Với ba điểm \(A,B,C\) tuỳ ý ta luôn có:
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\) (Quy tắc ba điểm)
\(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}\) (Quy tắc trừ)
5. Áp dụng
- Điểm \(I\) là trung điểm của đoạn thẳng \(AB\) khi và chỉ khi \(\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}\) ;
- Điểm \(G\) là trọng tâm của tam giác \(ABC\) khi và chỉ khi \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\).
@1950297@
III. TÍCH CỦA VECTƠ VỚI MỘT SỐ
1. Định nghĩa
Cho số \(k\ne0\) và vectơ \(\overrightarrow{a}\ne\overrightarrow{0}\). Tích của vectơ \(\overrightarrow{a}\) với số \(k\) là một vectơ, kí hiệu là \(k\overrightarrow{a}\), cùng hướng với \(\overrightarrow{a}\) nếu \(k>0\), ngược hướng với \(\overrightarrow{a}\) nếu \(k< 0\) và có độ dài bằng \(\left|k\right|\left|\overrightarrow{a}\right|\).
Quy ước \(0.\overrightarrow{a}=\overrightarrow{0}\) , \(k\overrightarrow{0}=\overrightarrow{0}\).
2. Tính chất
Với hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) bất kì, với mọi số \(h\) và \(k\), ta có:
\(k\left(\overrightarrow{a}+\overrightarrow{b}\right)=k\overrightarrow{a}+k\overrightarrow{b}\) ;
\(\left(h+k\right)\overrightarrow{a}=h\overrightarrow{a}+k\overrightarrow{a}\) ;
\(h\left(k\overrightarrow{a}\right)=\left(hk\right)\overrightarrow{a}\) ;
\(1.\overrightarrow{a}=\overrightarrow{a},\left(-1\right).\overrightarrow{a}=-\overrightarrow{a}\).
3. Trung điểm của đoạn thẳng và trọng tâm của tam giác
- Nếu \(I\) là trung điểm của đoạn thẳng \(AB\) thì với mọi điểm \(M\) ta có \(\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\)
- Nếu \(G\) là trọng tâm của tam giác \(ABC\) thì với mọi điểm \(M\) ta có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\).
4. Điều kiện để hai vectơ cùng phương
Điều kiện cần và đủ để hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) (\(\overrightarrow{b}\ne\overrightarrow{0}\)) cùng phương là có một số \(k\) để \(\overrightarrow{a}=k\overrightarrow{b}\).
Nhận xét: Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi có số \(k\) khác 0 để \(\overrightarrow{AB}=k\overrightarrow{AC}\).
5. Phân tích một vectơ theo hai vectơ không cùng phương
Cho hai vectơ không cùng phương \(\overrightarrow{a}\) và \(\overrightarrow{b}\). Khi đó mọi vectơ \(\overrightarrow{x}\) đều phân tích được một cách duy nhất theo hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\), nghĩa là có duy nhất cặp số \(h,k\) sao cho \(\overrightarrow{x}=h\overrightarrow{a}+k\overrightarrow{b}\).

@1950979@
IV. HỆ TRỤC TOẠ ĐỘ
1. Trục và độ dài đại số trên trục
- Trục toạ độ (hay gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm \(O\) gọi là điểm gốc và một vectơ đơn vị \(\overrightarrow{e}\). Ta kí hiệu trục đó là \(\left(O;\overrightarrow{e}\right)\).

- Cho \(M\) là một điểm tuỳ ý trên trục\(\left(O;\overrightarrow{e}\right)\). Khi đó có duy nhất một số \(k\) sao cho \(\overrightarrow{OM}=k\overrightarrow{e}\). Ta gọi số \(k\) đó là toạ độ của điểm \(M\) đối với trục đã cho.
- Cho hai điểm \(A\) và \(B\) trên trục \(\left(O;\overrightarrow{e}\right)\). Khi đó có duy nhất số \(a\) sao cho \(\overrightarrow{AB}=a\overrightarrow{e}\). Ta gọi số \(a\) đó là độ dài đại số của vectơ \(\overrightarrow{AB}\) đối với trục đã cho và kí hiệu là \(a=\overline{AB}\).
Nhận xét: Nếu \(\overrightarrow{AB}\) cùng hướng với \(\overrightarrow{e}\) thì \(\overline{AB}=AB\), còn nếu \(\overrightarrow{AB}\) ngược hướng với \(\overrightarrow{e}\) thì \(\overline{AB}=-AB\).
- Nếu hai điểm \(A\) và \(B\) trên trục \(\left(O;\overrightarrow{e}\right)\) có toạ độ lần lượt là \(a\) và \(b\) thì \(\overline{AB}=b-a\).
2. Hệ trục toạ độ
- Định nghĩa: Hệ trục toạ độ \(\left(O;\overrightarrow{i};\overrightarrow{j}\right)\) gồm hai trục \(\left(O;\overrightarrow{i}\right)\) và \(\left(O;\overrightarrow{j}\right)\) vuông góc với nhau. Điểm gốc \(O\) chung của hai trục gọi là gốc toạ độ. Trục \(\left(O;\overrightarrow{i}\right)\) được gọi là trục hoành và kí hiệu là \(Ox\), trục \(\left(O;\overrightarrow{j}\right)\) được gọi là trục tung và kí hiệu là \(Oy\). Các vectơ \(\overrightarrow{i}\) và \(\overrightarrow{j}\) là các vectơ đơn vị trên \(Ox\) và \(Oy\) và \(\left|\overrightarrow{i}\right|=\left|\overrightarrow{j}\right|=1\). Hệ trục toạ độ\(\left(O;\overrightarrow{i};\overrightarrow{j}\right)\) còn được kí hiệu là \(Oxy\).
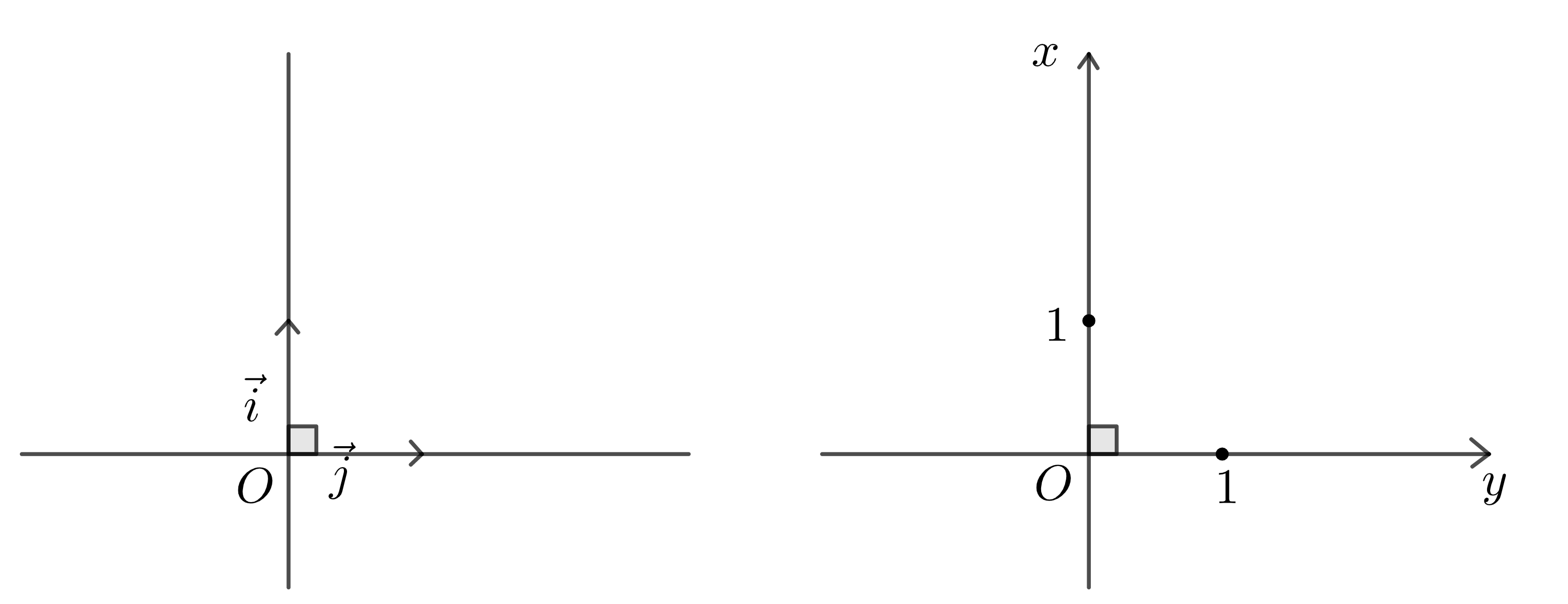
Mặt phẳng mà trên đó đã cho một hệ toạ độ \(Oxy\) được gọi là mặt phẳng toạ độ \(Oxy\) hay gọi tắt là mặt phẳng \(Oxy\).
- Toạ độ của vectơ: \(\overrightarrow{u}=\left(x;y\right)\Leftrightarrow\overrightarrow{u}=x\overrightarrow{i}+y\overrightarrow{j}\)
Ta gọi \(x\) là hoành độ, \(y\) là tung độ của vectơ \(\overrightarrow{u}\).
- Hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.
Nếu \(\overrightarrow{u}=\left(x;y\right)\) và \(\overrightarrow{u'}=\left(x';y'\right)\) thì \(\overrightarrow{u}=\overrightarrow{u'}\Leftrightarrow\left\{{}\begin{matrix}x=x'\\y=y'\end{matrix}\right.\).
- Toạ độ của điểm \(M\): \(M=\left(x;y\right)\Leftrightarrow\overrightarrow{OM}=x\overrightarrow{i}+y\overrightarrow{j}\)
Ta gọi \(x\) là hoành độ của điểm \(M\) và được kí hiệu là \(x_M\), \(y\) là tung độ của điểm \(M\) và được kí hiệu là \(y_M\).
- Cho hai điểm \(A\left(x_A;y_A\right)\) và \(B\left(x_B;y_B\right)\). Ta có
\(\overrightarrow{AB}=\left(x_B-x_A;y_B-y_A\right)\)
3. Toạ độ các vectơ \(\overrightarrow{u}+\overrightarrow{v}\), \(\overrightarrow{u}-\overrightarrow{v}\), \(k\overrightarrow{u}\)
Cho \(\overrightarrow{u}=\left(u_1;u_2\right)\) và \(\overrightarrow{v}=\left(v_1;v_2\right)\). Khi đó:
\(\overrightarrow{u}+\overrightarrow{v}=\left(u_1+v_1;u_2+v_2\right)\) ;
\(\overrightarrow{u}-\overrightarrow{v}=\left(u_1-v_1;u_2-v_2\right)\) ;
\(k\overrightarrow{u}=\left(ku_1;ku_2\right),k\in R\).
Ví dụ: Cho các vectơ \(\overrightarrow{a}=\left(1;-1\right)\), \(\overrightarrow{b}=\left(2;1\right)\), \(\overrightarrow{c}=\left(4;-1\right)\).
Ta có thể phân tích vectơ \(\overrightarrow{c}\) theo hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) là: \(\overrightarrow{c}=2\overrightarrow{a}+\overrightarrow{b}\).
4. Toạ độ trung điểm của đoạn thẳng. Toạ độ trọng tâm của tam giác
- Cho đoạn thẳng \(AB\) có \(A\left(x_A;y_A\right)\) và \(B\left(x_B;y_B\right)\). Toạ độ trung điểm \(I\left(x_I;y_I\right)\) của đoạn thẳng \(AB\) là:
\(x_I=\dfrac{x_A+x_B}{2};y_I=\dfrac{y_A+y_B}{2}\).
- Cho tam giác \(ABC\) có \(A\left(x_A;y_A\right)\), \(B\left(x_B;y_B\right)\) và \(C\left(x_C;y_C\right)\). Toạ độ trọng tâm \(G\left(x_G;y_G\right)\) của tam giác \(ABC\) là:
\(x_G=\dfrac{x_A+x_B+x_C}{3};y_G=\dfrac{y_A+y_B+y_C}{3}\).
@1950387@