Phương trình a x + b = 0 có nghiệm khi:
A. a ≠ 0
B. a = 0 , b ≠ 0
C. a = b = 0 a ≠ 0
D. a = b = 0
Cho 2 phương trình x^2+ax+12=0 và x^2+bx+7=0 có nghiệm chung. Khi đó A= 2a+3b+4 min=?
Cho a,b là nghiệm của phương trình x^2+5x-8=0 có a/b+1 và b/a+1 là
Viết chương trình giải phương trình ax + b = 0 (các hệ số a,b được nhập từ bàn phím)
Hướng dẫn có sẵn trong bài là:
- Nếu a khác 0 thì phương trình có nghiệm x=-b/a(âm b phần a)
- Nếu a = 0 và b = 0 thì phương trình có vô số nghiệm
- Nếu a = 0 và b khác 0 thì phương trình vô nghiệm
uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else
if (a=0 and b#0) then write('pt vo nghiem')
else
write(nghiẹm la x=': -b/a);
readln
end.
uses crt;
var a, b: logint;
Begin
write('nhap so a ='); Readln(a);
write('nhap so b ='); readln(b);
If (a = 0 and b = 0)
then write ('pt co nghiem x thuoc R')
else
if (a=0 and b#0) then write('pt vo nghiem')
else
write(nghiẹm la x=': -b/a);
readln
end.
biết rằng phương trình \(x^2+px+1=0\) có nghiệm là a,b và phương trình \(x^2+qx+2=0\) có nghiêm là b,c . Khi đó giá trị của biểu thức \(A=pq-\left(b-a\right)\left(b-c\right)\)bằng ?
Áp dụng viet vào pt \(x^2+px+1=0\) ta được:\(\left\{{}\begin{matrix}a+b=-p\\ab=1\end{matrix}\right.\)
Áp dụng viet vào pt \(x^2+qx+2=0\) ta được:\(\left\{{}\begin{matrix}b+c=-q\\bc=2\end{matrix}\right.\)
\(A=pq-\left(b-a\right)\left(b-c\right)=-\left(a+b\right).-\left(b+c\right)-\left(b^2-bc-ab+ac\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
\(=2ab+2bc=6\)
Phương trình: \(x^2+px+1=0\)
Có 2 nghiệm:a,b
\(\Rightarrow\left\{{}\begin{matrix}a+b=-p\\a.b=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}p=-\left(a+b\right)\\1=a.b\end{matrix}\right.\)
Phương trình \(x^2+px+2=0\)
Có 2 nghiệm:b,c
\(\Rightarrow\left\{{}\begin{matrix}b+c=-q\\b.c=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}q=-\left(b+c\right)\\2=b.c\end{matrix}\right.\)
Ta có: \(p.q-\left(b-a\right)\left(b-c\right)\)
\(=-\left(a+b\right).\left[-\left(b+c\right)\right]-\left(b-a\right)\left(b-c\right)\)
\(=\left(a+b\right)\left(b+c\right)-\left(b-a\right)\left(b-c\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
=\(\left(ab+ab\right)+\left(ac-ac\right)+\left(b^2-b^2\right)+\left(bc+bc\right)\)
\(=2ab+2bc\)
\(=2.1+2.2\)
=6
-Chúc bạn học tốt-
Cho hai phương trình
log 2 9 x - 4 = x log 2 3 + log 2 3 và 3 2 x - 3 x + 1 - 4 = 0 . Biết nghiệm chung của hai phương trình có dạng x = log a b ,với a , b > 0 , a + b < 10 .Khi đó
A. a+b= 9
B. a+b = 6
C. a+b = 5
D. a+b = 7
Cho phương trình: (m + 1) * x ^ 2 - 2(m - 1) * x + m - 2 = 0 (1)(x l hat a hat a n) a) Giải phương trình (1) khi m = 0 . b) Tìm giá trị của m để phương trình (1) có hai nghiệm phân biệt.
a. Bạn tự giải
b.
Phương trình có 2 nghiệm pb khi:
\(\left\{{}\begin{matrix}m+1\ne0\\\Delta'=\left(m+1\right)^2-\left(m+1\right)\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-1\\m>-1\end{matrix}\right.\) \(\Rightarrow m>-1\) (1)
c.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m+1}\\x_1x_2=\dfrac{m-2}{m+1}\end{matrix}\right.\)
Để biểu thức đề bài xác định \(\Rightarrow x_1x_2\ne0\Rightarrow m\ne2\), khi đó:
\(\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{7}{4}\Rightarrow\dfrac{x_1+x_2}{x_1x_2}=\dfrac{7}{4}\)
\(\Rightarrow4\left(x_1+x_2\right)=7x_1x_2\)
\(\Rightarrow\dfrac{8\left(m-1\right)}{m+1}=\dfrac{7\left(m-2\right)}{m+1}\)
\(\Rightarrow8\left(m-1\right)=7\left(m-2\right)\)
\(\Rightarrow m=-6< -1\) (ktm (1))
Vậy ko tồn tại m thỏa mãn yêu cầu đề bài
Cho phương trình a x 2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; △ ' = b ' 2 - ac. Phương trình đã cho có hai nghiệm phân biệt khi:
A. △ ' > 0
B. △ ' = 0
C. △ ' ≥ 0
D. △ ' ≤ 0
Đáp án A
Xét phương trình bậc hai a x 2 + bx + c = 0 (a ≠ 0) có biệt thức b = 2b'; Δ' = b ' 2 - ac:
• TH1: Nếu Δ' < 0 thì phương trình vô nghiệm
• TH2: Nếu Δ' = 0 thì phương trình có nghiệm kép
x
1
=
x
2
= 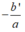
• TH3: Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt
x
1
,
2
= 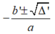
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2 b ’ ; Δ ' = b ' 2 − a c Phương trình đã cho có hai nghiệm phân biệt khi?
A. Δ ' > 0
B. Δ ' = 0
C. Δ ' ≥ 0
D. Δ ' ≤ 0
Xét phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0)
với b = 2b’ và biệt thức Δ ' = b ' 2 − a c
Trường hợp 1: Nếu ∆ < 0 thì phương trình vô nghiệm
Trường hợp 2: Nếu ∆ = 0 thì phương trình có nghiệm kép x1 = x2 = − b ' a
Trường hợp 3: nếu ∆ > 0 thì phương trình có hai nghiệm phân biệt
x1,2 = − b ' ± Δ ' a
Đáp án cần chọn là: A
Hai phương trình x 2 + a x + 1 = 0 v à x 2 - x - a = 0 có một nghiệm thực chung khi a bằng:
(A) 0 ; (B) 1 ; (C) 2 ; (D) 3
Hãy chọn câu trả lời đúng.
Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
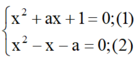
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.
Hai phương trình x 2 + a x + 1 = 0 v à x 2 - x - a = 0 có một nghiệm thực chung khi a bằng:
(A) 0 ; (B) 1 ; (C) 2 ; (D) 3
Hãy chọn câu trả lời đúng.
Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
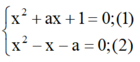
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.