Giúp mình với! Khó quá!
Cho hình thang ABCD(AB//CD) có \(\widehat{ADC}>\widehat{BCD}\).C/m AC>BD
Những câu hỏi liên quan
Hình thang ABCD có \(\widehat{D}=\widehat{A}=90^0\); AB = 30cm; CD = 18cm; BC = 20cm
a. Tính \(\widehat{ABC};\widehat{BCD}\)
b. Tính \(\widehat{DAC};\widehat{ADB}\)
c. Tính BD, AC
Cho hình thang ABCD có AB song song với CD . Gọi M, N lần lượt là trung điểm của hai đáy AB và CD thỏa mãn : MN=\(\frac{CD-AB}{2}\).
Chứng minh : \(\widehat{BCD}+\widehat{ADC}\) = 90 độ
Cho hình thang vuông ABCD(AB//CD,\(\widehat{A}=\widehat{D}=90\)độ ) có 2 đường chéo AC vuông góc với BD. c/m rằng : \(AD=\sqrt{AB.CD}\)
20 tháng 6 2019 lúc 10:46
Cho hình thang ABCD có đường cao AP và BQ cùng bằng đáy nhỏ AB (P,Q thuộc CD) và \(\widehat{BCD}+\widehat{ADC}=90^o\). Gọi E và F lần lượt là giao điểm của AP và BD; BQ và AC. Đường thẳng EF cắt AD và BC ở M,N. Chứng minh: EM = FN.
Cho hình thang ABCD có Ab song song CD và AB nhỏ hơn CD. Gọi M, N lần lượt là trung điểm của 2 đáy AB và CD thỏa mãn MN=\(\dfrac{CD-AB}{2}\)
Chứng tỏ \(\widehat{BCD}+\widehat{ADC}=90^0\)
SGK Cánh Diều
14 tháng 8 2023 lúc 0:00
Cho hình tứ diện ABCD có AB a,BC b,BD c,widehat {ABC} widehat {ABD} widehat {BCD} {90^ circ }. Gọi M,N,P lần lượt là trung điểm của AB,AC,AD (Hình 77).a) Tính khoảng cách từ điểm C đến đường thẳng AB.b) Tính khoảng cách từ điểm D đến mặt phẳng left( {ABC} right).c) Tính khoảng cách giữa hai đường thẳng AB và C{rm{D}}.
Đọc tiếp
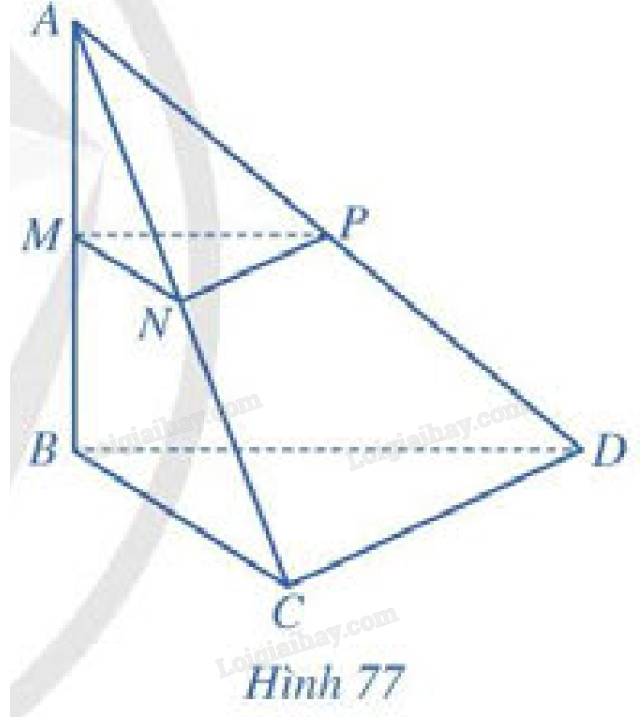
Cho hình tứ diện \(ABCD\) có \(AB = a,BC = b,BD = c\),\(\widehat {ABC} = \widehat {ABD} = \widehat {BCD} = {90^ \circ }\). Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,AC,AD\) (Hình 77).
a) Tính khoảng cách từ điểm \(C\) đến đường thẳng \(AB\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {ABC} \right)\).
c) Tính khoảng cách giữa hai đường thẳng \(AB\) và \(C{\rm{D}}\).
a) \(\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC \Rightarrow d\left( {C,AB} \right) = BC = b\).
b)
\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABC} = {90^ \circ } \Rightarrow AB \bot BC\\\widehat {ABD} = {90^ \circ } \Rightarrow AB \bot BD\end{array} \right\} \Rightarrow AB \bot \left( {BC{\rm{D}}} \right)\\\left. \begin{array}{l} \Rightarrow AB \bot C{\rm{D}}\\\widehat {BC{\rm{D}}} = {90^ \circ } \Rightarrow BC \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {ABC} \right)\\ \Rightarrow d\left( {D,\left( {ABC} \right)} \right) = C{\rm{D}} = \sqrt {B{{\rm{D}}^2} - B{C^2}} = \sqrt {{c^2} - {b^2}} \end{array}\)
c) \(AB \bot BC,C{\rm{D}} \bot BC \Rightarrow d\left( {AB,C{\rm{D}}} \right) = BC = b\).
Đúng 0
Bình luận (0)
CHO TỨ GIÁC LỒI ABCD KHÔNG CÓ 2 CẠNH NÀO SONG SONG VÀ \(\widehat{BAD}+\widehat{BCD}=\widehat{ABC}+\widehat{ADC}\). HAI ĐG CHÉO CẮT NHAU Ở O, CÁC ĐG THẲNG AB, CD CẮT NHAU Ở Q.
A) CM AB*CD+AD*BC=AC*BD
B) CM \(OA\cdot OC+OQ^2=QC\cdot QD\)
CHO TỨ GIÁC LỒI ABCD KHÔNG CÓ 2 CẠNH NÀO SONG SONG VÀ \(\widehat{BAD}+\widehat{BCD}=\widehat{ABC}+\widehat{ADC}\). HAI ĐG CHÉO CẮT NHAU Ở O, CÁC ĐG THẲNG AB, CD CẮT NHAU Ở Q.
A) CM AB*CD+AD*BC=AC*BD
B) CM \(OA\cdot OC+OQ^2=QC\cdot QD\)
Cho tứ giác ABCD ABBCAD , vàwidehat{DAB} + widehat{BCD} ^{^{ }180^o} a) Chứng minh rằng DB là tia phân giác của góc widehat{ADC} ?b) Chứng minh rằng tứ giác ABCD là hình thang cân ?
Đọc tiếp
Cho tứ giác ABCD \(AB=BC=AD\) , và\(\widehat{DAB}\) + \(\widehat{BCD}\) = \(^{^{ }180^o}\)
a) Chứng minh rằng DB là tia phân giác của góc \(\widehat{ADC}\) ?
b) Chứng minh rằng tứ giác ABCD là hình thang cân ?
a. Ta có: AD = AB
=> \(\Delta ABD\) là tam giác cân
=> Góc ADB = góc ABD (1)
Mà góc ABD = góc BDC (so le trong) (2)
Từ (1) và (2), suy ra:
BD là tia phân giác của góc ADC
b. Nối AC
Xét 2 tam giác ABC và ABD có:
AD = BC (gt)
AB chung
=> \(\Delta ABD\sim\Delta ABC\) (1)
Ta có: AD = AB = BC (2)
Từ (1) và (2), suy ra: \(\Delta ABD=\Delta ABC\)
=> Góc A = góc B
Ta có: AB//CD
=> Góc D + góc A = 90o (2 góc trong cùng phía)
Mà góc A = góc B
=> Góc C = góc D
=> ABCD là hình thang cân
Đúng 2
Bình luận (2)
Nhưng bậy giờ bn chỉ cần chứng minh đó là hình thang là đc
Đúng 0
Bình luận (1)
Xem thêm câu trả lời