Giải phương trình: \(\frac{x^4+x^3+x+1}{x^4-x^3+2x^2-x+1}\le0\)

Những câu hỏi liên quan
Giải các bất phương trình sau
1) \(\dfrac{\text{x - 2}}{x+1}-\dfrac{3}{x+2}>0\) 2) \(\dfrac{\text{x + 1}}{x+2}+\dfrac{x}{x-3}\le0\)
3) \(\dfrac{\text{x}^2+2x+5}{x+4}>x-3\) 4) \(\sqrt{\text{x^2}-3x+2}\ge3\)
\(\dfrac{x-2}{x+1}-\dfrac{3}{x+2}>0.\left(x\ne-1;-2\right).\\ \Leftrightarrow\dfrac{x^2-4-3x-3}{\left(x+1\right)\left(x+2\right)}>0.\\ \Leftrightarrow\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{x^2-3x-7}{\left(x+1\right)\left(x+2\right)}>0.\)
Ta có: \(x^2-3x-7=0.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3+\sqrt{37}}{2}.\\x=\dfrac{3-\sqrt{37}}{2}.\end{matrix}\right.\)
\(x+1=0.\Leftrightarrow x=-1.\\ x+2=0.\Leftrightarrow x=-2.\)
Bảng xét dấu:
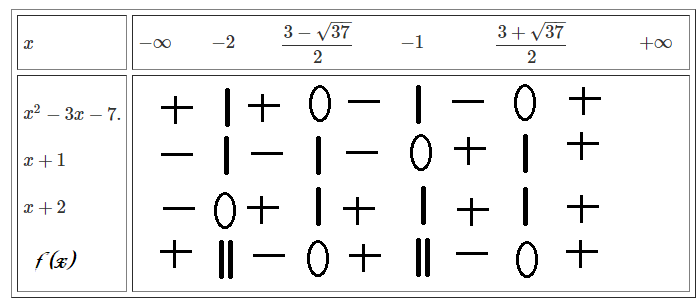
\(\Rightarrow f\left(x\right)>0\Leftrightarrow x\in\left(-\infty-2\right)\cup\left(\dfrac{3-\sqrt{37}}{2};-1\right)\cup\left(\dfrac{3+\sqrt{37}}{2};+\infty\right).\)
\(\sqrt{x^2-3x+2}\ge3.\\ \Leftrightarrow x^2-3x+2\ge9.\\ \Leftrightarrow x^2-3x-7\ge0.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3-\sqrt{37}}{2}.\\x=\dfrac{3+\sqrt{37}}{2}.\end{matrix}\right.\)
Đặt \(f\left(x\right)=x^2-3x-7.\)
\(f\left(x\right)=x^2-3x-7.\)
\(\Rightarrow f\left(x\right)\ge0\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
\(\Rightarrow\sqrt{x^2-3x+2}\ge3\Leftrightarrow x\in(-\infty;\dfrac{3-\sqrt{37}}{2}]\cup[\dfrac{3+\sqrt{37}}{2};+\infty).\)
Đúng 1
Bình luận (0)
giải bất phương trình:
a)\(\frac{2x+1}{x-1}-2\le0\)
b)\(\frac{\left(x-2\right)\left(2x+3\right)}{1-x}\le0\)
c)\(\frac{2}{x-1}\le\frac{5}{2x-1}\)
e)\(\frac{1}{x}+\frac{2}{x+4}< \frac{3}{x+3}\)
f)\(\frac{x+2}{3x+1}\le\frac{x-2}{2x-1}\)
https://i.imgur.com/NIunWu5.jpg
https://i.imgur.com/m9wCgfC.jpg
Áp dụng giải bất phương trình
\(\dfrac{\left(2x+1\right)^4\left(x-3\right)^3}{\left(x+5\right)^2x^5}\le0\)
Lời giải:
ĐK: $x\neq -5; n\neq 0$
\(\frac{(2x+1)^4(x-3)^3}{(x+5)^2x^5}\leq 0\Leftrightarrow \left[\frac{(2x+1)^2(x-3)}{(x+5)x^2}\right]^2.\frac{x-3}{x}\leq 0\)
\(\Leftrightarrow \frac{x-3}{x}\leq 0\Rightarrow \left[\begin{matrix} x-3\geq 0; x< 0\\ x-3\leq 0; x>0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} 0> x\geq 3(\text{vô lý})\\ 3\geq x>0\end{matrix}\right.\)
Vậy $3\geq x>0$
Đúng 0
Bình luận (0)
Giải bất phương trình
1) \(\frac{x^4-1}{x^2+3x}+x^2\ge1\)
2) \(\left(x^4-5x^2+4\right)\left(\frac{x-2}{x}-3\right)\le0\)
3) \(\left(\frac{4}{x}-\frac{2}{x-1}\right)\left(\frac{x^2+1}{x}-2\right)\le0\)
4) \(\left(\sqrt{x^3-4x}-\sqrt{15}\right)\sqrt{\frac{1+x}{x}-2}\le0\)
a/
\(\Leftrightarrow\frac{\left(x^2-1\right)\left(x^2+1\right)}{x^2+3x}+x^2-1\ge0\)
\(\Leftrightarrow\left(x^2-1\right)\left(\frac{x^2+1}{x^2+3x}+1\right)\ge0\)
\(\Leftrightarrow\left(x^2-1\right)\left(\frac{2x^2+3x+1}{x^2+3x}\right)\ge0\)
\(\Leftrightarrow\frac{\left(x-1\right)\left(x+1\right)\left(x+1\right)\left(2x+1\right)}{x\left(x+3\right)}\ge0\)
\(\Leftrightarrow\frac{\left(x-1\right)\left(2x+1\right)\left(x+1\right)^2}{x\left(x+3\right)}\ge0\)
\(\Rightarrow\left[{}\begin{matrix}x< -3\\x=-1\\-\frac{1}{2}\le x< 0\\x\ge1\end{matrix}\right.\)
b/
\(\Leftrightarrow\left(x^2-1\right)\left(x^2-4\right)\left(\frac{-2-2x}{x}\right)\le0\)
\(\Leftrightarrow\frac{-2.\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\left(x+1\right)}{x}\le0\)
\(\Leftrightarrow\frac{\left(x+2\right)\left(x-1\right)\left(x-2\right)\left(x+1\right)^2}{x}\ge0\)
\(\Rightarrow\left[{}\begin{matrix}x\le-2\\x=-1\\0< x\le1\\x\ge2\end{matrix}\right.\)
c/
\(\Leftrightarrow\left(\frac{4\left(x-1\right)-2x}{x\left(x-1\right)}\right)\left(\frac{x^2+1-2x}{x}\right)\le0\)
\(\Leftrightarrow\frac{\left(2x-4\right)\left(x-1\right)^2}{x^2\left(x-1\right)}\le0\)
\(\Leftrightarrow\frac{\left(x-2\right)\left(x-1\right)^2}{x^2\left(x-1\right)}\le0\)
\(\Rightarrow1< x\le2\)
d/
ĐKXĐ: \(\left\{{}\begin{matrix}x^3-4x\ge0\\\frac{1+x}{x}-2\ge0\\x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\left(x-2\right)\left(x+2\right)\ge0\\\frac{1-x}{x}\ge0\\x\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}-2\le x\le0\\x\ge2\end{matrix}\right.\\0< x\le1\\x\ne0\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại x thỏa mãn ĐKXĐ
Vậy BPT đã cho vô nghiệm
Giải các bất phương trình sau:
a. \(\left(1-2x\right)\left(x^2+x-30\right)\left(x^2-4x+4\right)\le0\)
b. \(\frac{1}{x^2-5x+4}< \frac{1}{x^2-7x+6}\)
c. \(\frac{2}{x^2-x+1}-\frac{1}{x-1}\ge\frac{2x-1}{x^3+a}\)
Giúp mình với ạ
a) Giải phương trình: \(\frac{x^2}{2}+\frac{x}{2}+1=\sqrt{2x^3-x^2+x+1}\)
b) Giải hệ phương trình \(\hept{\begin{cases}2x+3+\sqrt{4-y}=4\\\sqrt{2y+3}+\sqrt{4-x}=4\end{cases}}\)
Giải Phương trình
a, \(\frac{x+4}{2x^2-5x+2}+\frac{x+1}{2x^2-7x+3}=\frac{2x+5}{2x^2-7x+3}\)
b, \(\frac{x^2}{x^2+2x+2}+\frac{x^2}{x^2-2x+2}-\frac{4.\left(x^2-5\right)}{x^4+4}=\frac{322}{65}\)
c, \(\frac{1}{x-1}+\frac{2x^2-5}{x^3-1}=\frac{4}{x^2+x+1}\)
Trình bày cách làm nữa nha
Bài 1: Giải phương trình
1) \(\sqrt{4x^2+12x+9}=2-x\left(vớix\le0\right)\)
2) \(\sqrt{x^4+2x^2+1}=x^2+5x+4\) ( với \(x^2+5x+4>0\))
3) \(\sqrt{5x+1}=4\)
4) \(\sqrt{3-x}=7\)
Câu 2,3,4 nx thôi ạ. Câu 1 có bạn giúp r ạ
Đúng 0
Bình luận (0)
1)\(\sqrt{4x^2+12x+9}=2-x\)
\(\Leftrightarrow\sqrt{\left(2x+3\right)^2}=2-x\)
\(\Leftrightarrow\left|2x+3\right|=2-x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+3=2-x\\2x+3=x-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=-1\\x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-5\end{matrix}\right.\)
\(\)
Đúng 0
Bình luận (1)
2)\(\sqrt{x^4+2x^2+1}=x^2+5x+4\) ĐK:\(x\ge-1\)
\(\Leftrightarrow\sqrt{\left(x^2+1\right)^2}=x^2+5x+4\)
\(\Leftrightarrow\left|x^2+1\right|=x^2+5x+4\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=x^2+5x+4\\x^2+1=-x^2-5x-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}5x=-3\\2x^2+5x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{5}\\2\left(x+\dfrac{5}{4}\right)^2+\dfrac{15}{8}=0\left(voli\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải hệ phương trình: \(\hept{\begin{cases}\sqrt{2x^2y^2-x^4y^4}=y^6+x^2\left(1-x\right)\\\sqrt{1+\left(x+y\right)^2}+x\left(2y^3+x^2\right)\le0\end{cases}}\)



















