Ai đồ Sử nào giúp mềnh với ạ, mềnh xin tặng 5coin ạ!
Mềnh cần gấp ạ, giúp mềnh mềnh xin biếu 5coin mần quà :))
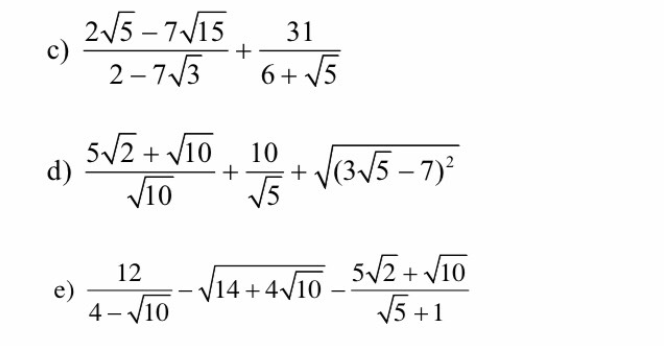
c) \(=\dfrac{\sqrt{5}\left(2-7\sqrt{3}\right)}{2-7\sqrt{3}}+\dfrac{31\left(6-\sqrt{5}\right)}{36-5}=\sqrt{5}+6-\sqrt{5}=6\)
d) \(=\dfrac{\sqrt{10}\left(\sqrt{5}+1\right)}{\sqrt{10}}+\dfrac{10\sqrt{5}}{5}+\left|3\sqrt{5}-7\right|=\sqrt{5}+1+2\sqrt{5}+7-3\sqrt{5}=8\)
e) \(=\dfrac{12\left(4+\sqrt{10}\right)}{16-10}-\sqrt{\left(\sqrt{10}+2\right)^2}-\dfrac{\sqrt{10}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}=2\left(4+\sqrt{10}\right)-\sqrt{10}-2-\sqrt{10}=6\)
P/s: Nhớ lời hứa nha bé =))
c) \(\dfrac{2\sqrt{5}-7\sqrt{15}}{2-7\sqrt{3}}+\dfrac{31}{6+\sqrt{5}}=\dfrac{\sqrt{5}\left(2-7\sqrt{3}\right)}{2-7\sqrt{3}}+\dfrac{31}{6+\sqrt{5}}=\sqrt{5}+\dfrac{31}{6+\sqrt{5}}=\dfrac{\sqrt{5}\left(6+\sqrt{5}\right)+31}{6+\sqrt{5}}=\dfrac{6\sqrt{5}+36}{6+\sqrt{5}}=\dfrac{6\left(\sqrt{5}+6\right)}{6+\sqrt{5}}=6\)
d) \(\dfrac{5\sqrt{2}+\sqrt{10}}{\sqrt{10}}+\dfrac{10}{\sqrt{5}}+\sqrt{\left(3\sqrt{5}-7\right)^2}=\dfrac{\sqrt{10}\left(\sqrt{5}+1\right)}{\sqrt{10}}+\dfrac{\sqrt{100}}{\sqrt{5}}+\sqrt{\left(7-3\sqrt{5}\right)^2}=\sqrt{5}+1+2\sqrt{5}+7-3\sqrt{5}=8\)
e) \(\dfrac{12}{4-\sqrt{10}}-\sqrt{14+4\sqrt{10}}-\dfrac{5\sqrt{2}+\sqrt{10}}{\sqrt{5}+1}=\dfrac{\sqrt{144}}{\sqrt{16}-\sqrt{10}}-\sqrt{14+2\sqrt{40}}-\dfrac{\sqrt{50}+\sqrt{10}}{\sqrt{5}+1}=\dfrac{\sqrt{144}}{\sqrt{2}\left(\sqrt{8}-\sqrt{5}\right)}-\sqrt{10+2\sqrt{10}.\sqrt{4}+4}-\dfrac{\sqrt{10}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}=\dfrac{\sqrt{72}}{\sqrt{8}-\sqrt{5}}-\sqrt{10}-2-\sqrt{10}=\dfrac{\sqrt{72}}{\sqrt{8}-\sqrt{5}}-2\sqrt{10}-2=6\)
Giúp mềnh câu c nha, mềnh xin tặng 5coin mần quà :>
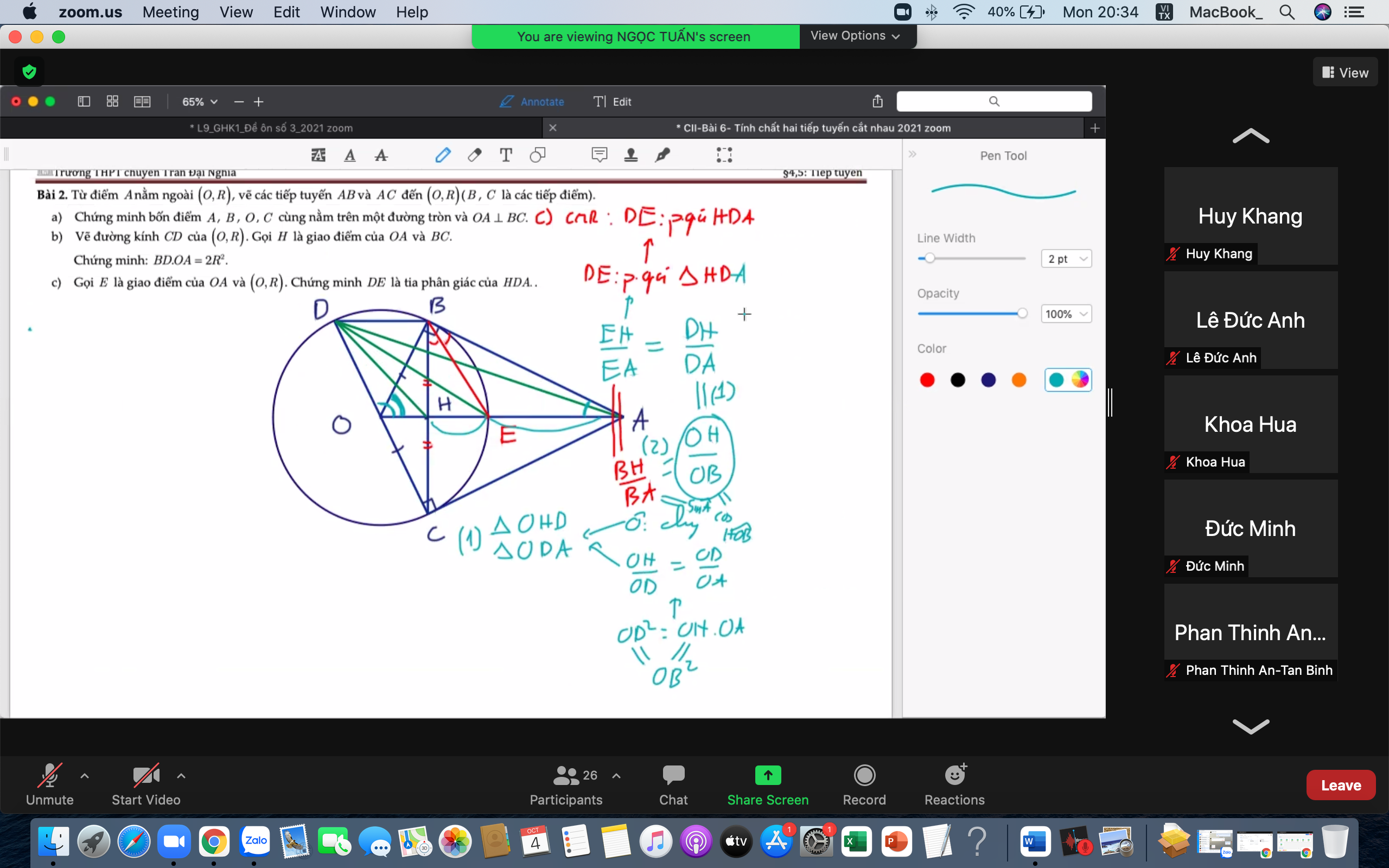
Ta có: \(\widehat{DBC}=90^0\) (nt chắn nửa đường tròn)
\(\Rightarrow BD||OA\) (cùng vuông góc BC)
\(\Rightarrow\widehat{BDE}=\widehat{DEO}\) (slt)
Mà \(\widehat{DEO}=\widehat{ODE}\) (OD=OE=R nên tam giác ODE cân tại O)
\(\Rightarrow\widehat{ODE}=\widehat{BDE}\) (1)
Lại có OH là đường trung bình tam giác BCD (đi qua 2 trung điểm)
\(\Rightarrow BD=2OH\)
Theo câu b: \(BD.OA=2R^2=2OD^2\Rightarrow2OH.OA=2OD^2\)
\(\Rightarrow\dfrac{OH}{OD}=\dfrac{OD}{OA}\)
Hai tam giác ODH và OAD có: \(\left\{{}\begin{matrix}\widehat{O}\text{ chung}\\\dfrac{OH}{OD}=\dfrac{OD}{OA}\end{matrix}\right.\)
\(\Rightarrow\Delta ODH\sim\Delta OAD\Rightarrow\widehat{ODH}=\widehat{OAD}\)
Mà \(\widehat{OAD}=\widehat{BDA}\) (so le trong) (2)
(1);(2) \(\Rightarrow\widehat{HDE}=\widehat{ADE}\) hay DE là phân giác \(\widehat{HDA}\)
Giúp mềnh trong tối nay ạ, mềnh xin tặng 5 coin mần quà!

cho em coin đi ![]()
em ko bt giải hihi
em còn nhỏ
Khum cần coin đou e nha
IV
1 have known - was
2 have you read
3 have never seen
4 Have you already finished
5 has learned
6 has already given
7 have lived
8 haven't cleaned
9 has she learned
10 has taught
V
1 to go
2 studying
3 saw
4 was painted
5 didn't see
6 have played
7 has been read
8 get
9 getting
10 would have
11 cut
12 would come
13 has been
14 has been celebrated
15 were broken
Giúp mình vs ạ, mình xin tặng 5coin ạ :>
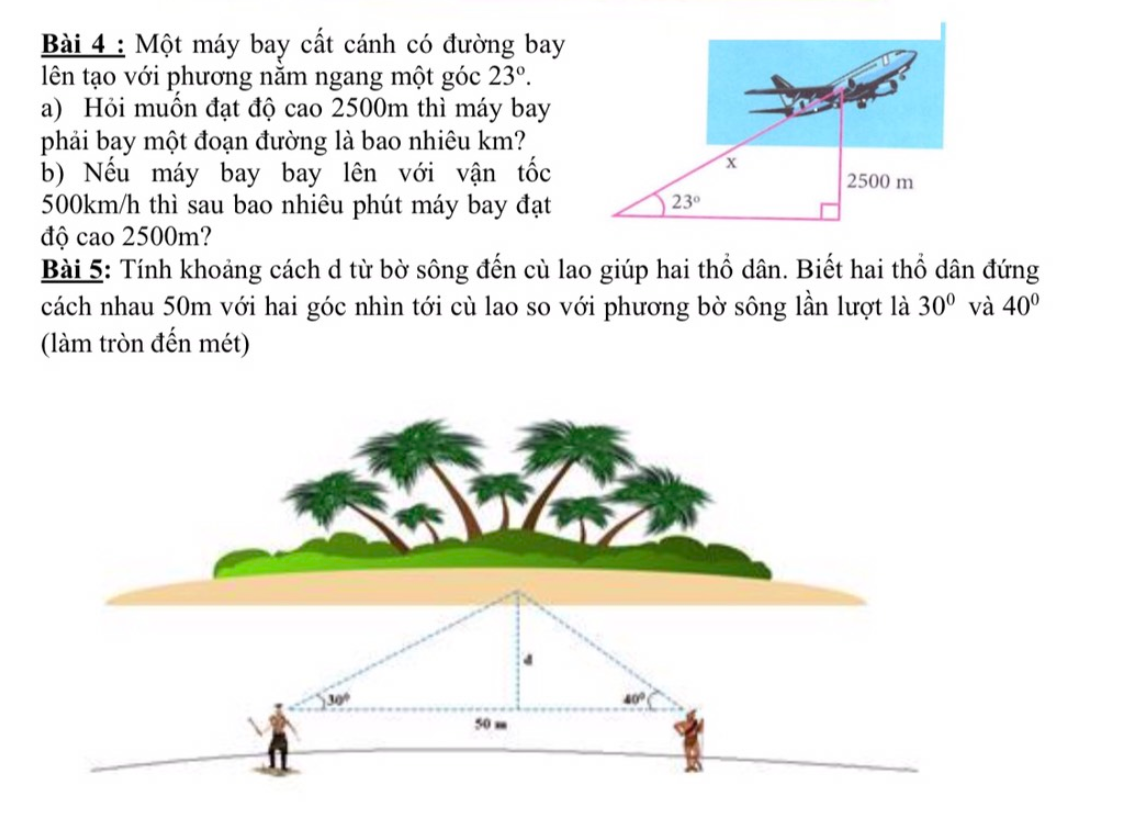
Bài 4:
a) Gọi AB là độ cao máy bay, BC là đoạn đường máy bay bay
Áp dụng tslg trong tam giác ABC vuông tại A:
\(sinC=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sinC}=\dfrac{2500}{sin23^0}\approx6398\left(m\right)\)
b) Đổi: \(6398m=6,398km\)
Thời gian máy bay đạt độ cao 2500m:
\(t=\dfrac{S}{v}=\dfrac{6,398}{500}\approx0,03h=1,8ph\)
Bài 5:
Gọi B là góc nhìn \(30^0\) và C là góc nhìn \(40^0\), A là cù lao, kẻ đường cao AH
Áp dụng tslg:
\(\left\{{}\begin{matrix}tanB=\dfrac{AH}{HB}\Rightarrow AH=HB.tan30^0\\tanC=\dfrac{AH}{HC}\Rightarrow AH=HC.tan40^0\end{matrix}\right.\)
\(\Rightarrow\dfrac{HB}{tan40^0}=\dfrac{HC}{tan30^0}=\dfrac{HB+HC}{tan40^0+tan30^0}=\dfrac{BC}{tan40^0+tan30^0}\approx35\left(m\right)\)
\(\Rightarrow HB\approx30\left(m\right)\Rightarrow AH\approx17\left(m\right)\)
Giúp mềnh câu c nha, mềnh xin tặng 2coin mần quà :>
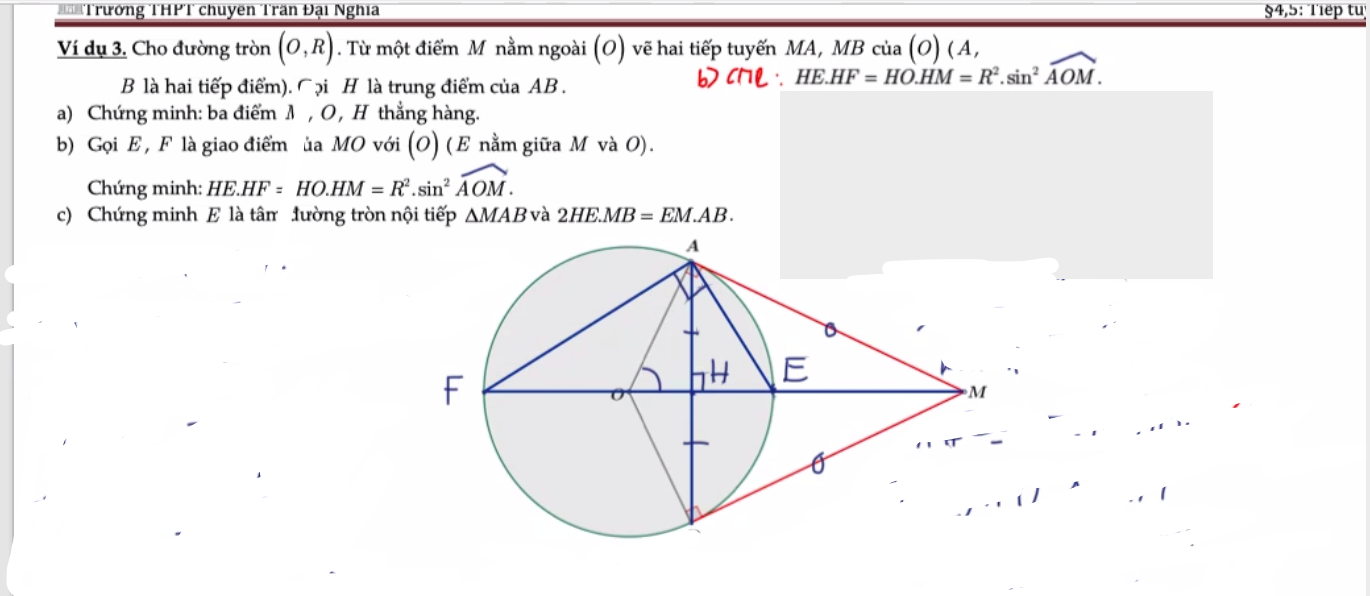
Theo t/c 2 tiếp tuyến \(AM=BM\Rightarrow\Delta ABM\) cân tại M
\(\Rightarrow MH\) là trung tuyến, đường cao, trung trực AB đồng thời là phân giác \(\widehat{AMB}\)
\(\Rightarrow AE=BE\Rightarrow\Delta ABE\) cân tại E
\(\Rightarrow\widehat{ABE}=\widehat{BAE}\)
Mà \(\widehat{ABE}=\widehat{MAE}\) (cùng chắn cung AE)
\(\Rightarrow\widehat{BAE}=\widehat{MAE}\Rightarrow AE\) là phân giác \(\widehat{BAM}\)
\(\Rightarrow\) E là giao điểm 2 đường phân giác trong của tam giác ABM hay E là tâm đường tròn nội tiếp tam giác
Theo định lý phân giác (trong tam giác AHM)
\(\dfrac{HE}{AH}=\dfrac{ME}{AM}\Rightarrow ME.AH=HE.AM\Rightarrow ME.\dfrac{AB}{2}=HE.BM\Rightarrow2HE.BM=ME.AB\)
ai có đề toán thi cuối học kì II cho mềnh xin với, cảm ơn các bạn nhìu
P/s: do ko có box lớp 5 nên..........mềnh đăng box 6 ạ
Giúp mềnh với ạ
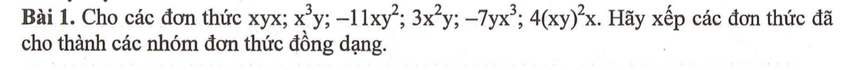 giúp mềnh với ạ=(((
giúp mềnh với ạ=(((
\(4\left(xy\right)^2\cdot x=4x^2y^2\cdot x=4x^3y^2\)
Nhóm 1: \(x^3y;-7x^3y\)
Nhóm 2: \(x^2y;3x^2y\)
 giúp mềnh với ạ
giúp mềnh với ạ