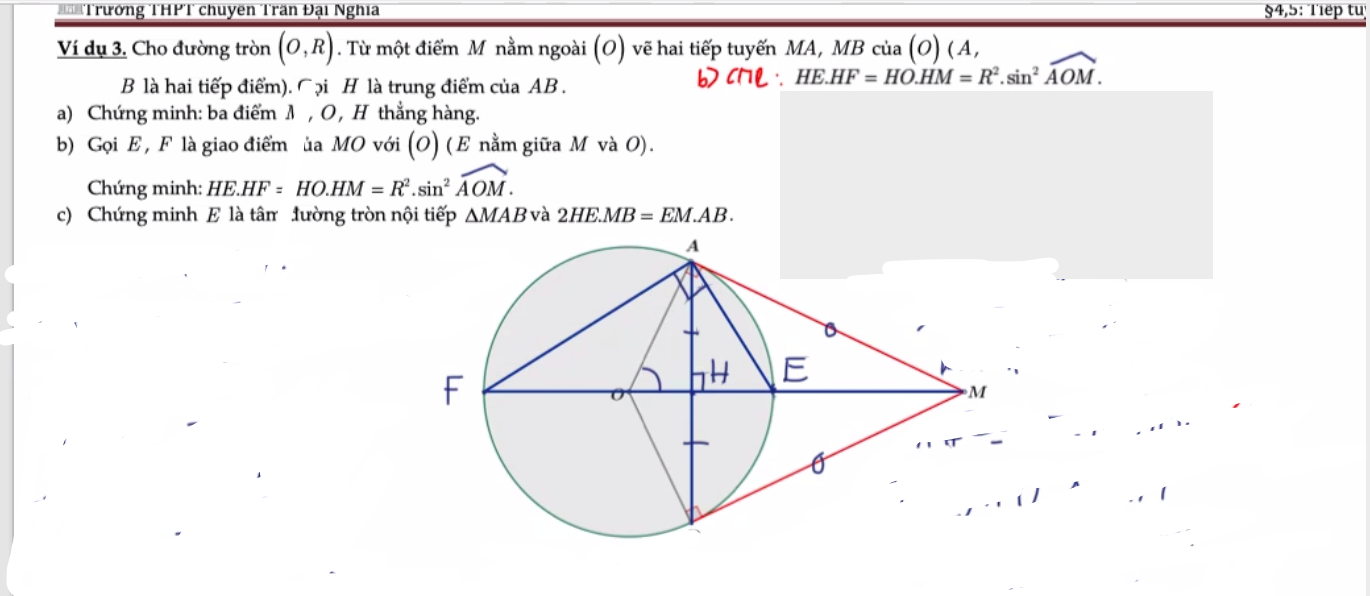
Theo t/c 2 tiếp tuyến \(AM=BM\Rightarrow\Delta ABM\) cân tại M
\(\Rightarrow MH\) là trung tuyến, đường cao, trung trực AB đồng thời là phân giác \(\widehat{AMB}\)
\(\Rightarrow AE=BE\Rightarrow\Delta ABE\) cân tại E
\(\Rightarrow\widehat{ABE}=\widehat{BAE}\)
Mà \(\widehat{ABE}=\widehat{MAE}\) (cùng chắn cung AE)
\(\Rightarrow\widehat{BAE}=\widehat{MAE}\Rightarrow AE\) là phân giác \(\widehat{BAM}\)
\(\Rightarrow\) E là giao điểm 2 đường phân giác trong của tam giác ABM hay E là tâm đường tròn nội tiếp tam giác
Theo định lý phân giác (trong tam giác AHM)
\(\dfrac{HE}{AH}=\dfrac{ME}{AM}\Rightarrow ME.AH=HE.AM\Rightarrow ME.\dfrac{AB}{2}=HE.BM\Rightarrow2HE.BM=ME.AB\)