Cho đường thẳng d: 2x+3y-1=0
Tìm M trên d sao cho OM=5
: Cho đường thẳng: (d): y = (2m – 1)x + m – 2.
1) Tìm m để đường thẳng (d):
a. Đi qua điểm A(1; 6).
b. Song song với đường thẳng 2x + 3y – 5 = 0.
c. Vuông góc với đường thẳng x + 2y + 1 = 0.
2) Tìm điểm cố định mà (d) luôn đi qua với mọi m.
mn giảng giúp mình với, tại mình không hiểu ý ạ:( camon mn nhiều ạ
1.
\(a,\Leftrightarrow2m-1+m-2=6\Leftrightarrow3m=9\Leftrightarrow m=3\\ b,2x+3y-5=0\Leftrightarrow3y=-2x+5\Leftrightarrow y=-\dfrac{2}{3}x+\dfrac{5}{3}\)
Để \(\left(d\right)\text{//}y=-\dfrac{2}{3}x+\dfrac{5}{3}\Leftrightarrow\left\{{}\begin{matrix}2m-1=-\dfrac{2}{3}\\m-2\ne\dfrac{5}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{1}{6}\\m\ne\dfrac{11}{3}\end{matrix}\right.\Leftrightarrow m=\dfrac{1}{6}\)
\(c,x+2y+1=0\Leftrightarrow2y=-x-1\Leftrightarrow y=-\dfrac{1}{2}x-\dfrac{1}{2}\\ \left(d\right)\bot y=-\dfrac{1}{2}x-\dfrac{1}{2}\Leftrightarrow\left(-\dfrac{1}{2}\right)\left(2m-1\right)=-1\\ \Leftrightarrow\dfrac{1}{2}\left(2m-1\right)=1\Leftrightarrow m-\dfrac{1}{2}=1\Leftrightarrow m=\dfrac{3}{2}\)
2.
Gọi điểm cố định đó là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(2m-1\right)x_0+m-2\\ \Leftrightarrow2mx_0+m-x_0-2-y_0=0\\ \Leftrightarrow m\left(2x_0+1\right)-\left(x_0+y_0+2\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x_0=-1\\x_0+y_0+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=-\dfrac{1}{2}\\y_0=-\dfrac{3}{2}\end{matrix}\right.\)
1. Cho M(3;-1) và đường thẳng d: 3x-4y+12=0. Tìm N đối xứng với M qua d.
2. Cho M(8;2) và đường thẳng d: 2x-3y+3=0. Tìm N đối xứng với M qua d.
3. Cho đường thẳng d: x+y-5=0 và I(2;0). Tìm điểm M thuộc d sao cho MI=3.
4. Cho tam giác ABC có M(2;-1) là trung điểm AB. Đường trung tuyến và đường cao qua A lần lượt là: d1: x+y-7=0 và d2: 5x+3y-29=0.
a.Tìm điểm A và viết pt cạnh BC.
b. Viết pt cạnh AC.
CÁC BẠN GIẢI GIÚP MÌNH VỚI NHÉ. CẢM ƠN
trl ; bạn kia đúng r
-
_
----------------
Trong hệ trục tọa độ (xOy), cho điểm G(2,0) và đường thẳng d x-3y+1=0 Tìm trên đường thẳng d điểm M sao cho OM là cạnh huyền của tam giác OMG
OM là cạnh huyền \(\Rightarrow OG\perp GM\)
Gọi \(M\left(3a-1;a\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{OG}=\left(2;0\right)\\\overrightarrow{GM}=\left(3a-3;a\right)\end{matrix}\right.\)
\(\overrightarrow{OG}.\overrightarrow{GM}=0\Leftrightarrow2\left(3a-3\right)=0\Leftrightarrow a=1\)
\(\Rightarrow M\left(2;1\right)\)
Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Tìm tọa độ của w → có giá vuông góc với đường thẳng d để d 1 là ảnh của d qua T w →
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Đường thẳng d 2 qua M vuông góc với có vectơ chỉ phương là v → = ( 2 ; − 3 ) .
Do đó phương trình của
d
2
là 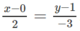 .
.
Gọi M' là giao của d 1 với d 2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
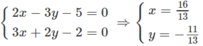
Từ đó suy ra
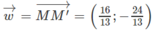
Cho đường tròn (C) x2+ y2- 2x + 6y + 6= 0 và đường thẳng d: 4x -3y + 5= 0. Đường thẳng d’ song song với đường thẳng d và chắn trên (C) một dây cung có độ dài bằng 2 3 có phương trình là:
A. 4x- 3y+ 8= 0
B.4x-3y- 8= 0 hoặc 4x – 3y -18= 0
C. 4x- 3y+ 10= 0
D. 4x + 3y + 8 = 0
Đáp án B
Đường tròn (C) có tâm I( 1; -3) và R= 2
![]() có phương trình 4x- 3y+ m= 0.
có phương trình 4x- 3y+ m= 0.
Vẽ
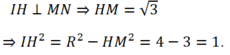
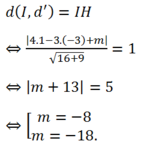

Vậy:
Trong mặt phẳng v → = ( − 2 ; 1 ) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d 1 có phương trình 2 x − 3 y − 5 = 0 .
Viết phương trình của đường thẳng d’ là ảnh của d qua T v → .
Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Khi đó M′ = T v → ( M ) = (0 − 2; 1 + 1) = (−2; 2) thuộc d'.
Vì d' song song với d nên phương trình của nó có dạng 2x − 3y + C = 0.
Do M' ∈ d′ nên 2.(−2) − 3.2 + C = 0. Từ đó suy ra C = 10 .
Do đó d' có phương trình 2x − 3y + 10 = 0.
Cho đường thẳng d có phương trình tổng quát là: x - 2y – 5 = 0.
a) Lập phương trình tham số của đường thẳng d.
b) Tìm toạ độ điểm M thuộc d sao cho OM = 5 với O là gốc toạ độ.
c) Tìm toạ độ điểm N thuộc d sao cho khoảng cách từ N đến trục hoành Ox là 3.
a) Từ phương trình tổng quát của đường thẳng, ta lấy được một vecto pháp tuyến là: \(\overrightarrow n = \left( {1; - 2} \right)\) nên ta chọn vecto chỉ phương của đường thẳng d là: \(\overrightarrow u = \left( {2;1} \right)\).
Chọn điểm \(A\left( {1; - 2} \right) \in d\).Vậy phương trình tham số của đường thẳng d là: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\end{array} \right.\) (t là tham số)
b) Do điểm M thuộc d nên ta có: \(M\left( {1 + 2m; - 2 + m} \right);m \in \mathbb{R}\).
Ta có: \(OM = 5 \Leftrightarrow \sqrt {{{\left( {1 + 2m} \right)}^2} + {{\left( { - 2 + m} \right)}^2}} = 5 \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2\)
Với \(m = 2 \Rightarrow M\left( {5;0} \right)\)
Với \(m = - 2 \Rightarrow M\left( { - 3; - 4} \right)\)
Vậy ta có 2 điểm M thỏa mãn điều kiện đề bài.
c) Do điểm N thuộc d nên ta có: \(N\left( {1 + 2n; - 2 + n} \right)\)
Khoảng cách từ N đến trục hoành bằng giá trị tuyệt đối của tung độ điểm N. Do đó, khoảng cách tư N đến trục hoành bằng 3 khi và chỉ khi: \(\left| { - 2 + n} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = - 1\end{array} \right.\)
Với \(n = 5 \Rightarrow N\left( {11;3} \right)\)
Với \(n = - 1 \Rightarrow N\left( { - 1; - 3} \right)\)
Vậy có 2 điểm N thỏa mãn bài toán
Cho đường thẩng (d): 2x+y-1=0 và điểm A(0; -2), B(2; 3).
1) Lập phương trình đường thẳng d1 đi qua A và song song với d.
2) Lập phương trình đường thẳng d2 đi qua B và vuông góc với d. Từ đó tìm tọa độ hình chiếu H của B trên d.
3) Tìm điểm M thuộc trục hoành sao cho khoảng cách từ M đến d bằng \(2√5 \).
4) Tìm điểm N thuộc d sao cho khoảng cách từ N đến A bằng 5.
Cho đường thẳng (d): y=ax+b
a) Tìm a,b sao cho (d) đi qua A(1;-1) và song song với đường thẳng y=2x+3
b) Vẽ đường thẳng (d)
c) Tìm m sao cho 3 đường thẳng (d) và y=x+1 và y=(m-1).x+5 đồng qui.
a: Vì (d)//y=2x+3 nên a=2
Vậy: (d): y=2x+b
Thay x=1 và y=-1 vào (d), ta được:
b+2=-1
hay b=-3
c. Gọi: \(\left[{}\begin{matrix}y=x+1\left(d'\right)\\y=\left(m-1\right)x+5\left(d''\right)\end{matrix}\right.\)
Ta có: \(PTHDGD:\left(d\right)-\left(d'\right)\)
\(2x+3=x+1\)
\(\Rightarrow x=-2\left(1\right)\)
\(Thay\left(1\right)in\left(d'\right):y=-2+1=-1\)
\(\Rightarrow A\left(-2;-1\right)\)
Để 3 đt này đồng quy, thì \(A\left(-2;-1\right)\in\left(d''\right)\Leftrightarrow-1=-2m+2+5\)
\(\Rightarrow m=4\)