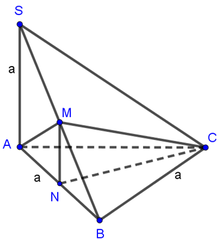
Cho SABC, SA⊥ (ABC), SA=a, tam giác ABC đều cạnh a. Tính d(SB,AC)

Những câu hỏi liên quan
cho hình chóp sabc có sa=sb=sc=2a, tam giác abc đều cạnh a. tính thể tích khối chóp sab
Gọi H là tâm đáy \(\Rightarrow SH\perp\left(ABC\right)\)
Ta có: \(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
Áp dụng định lý Pitago:
\(SH=\sqrt{SA^2-AH^2}=\dfrac{a\sqrt{33}}{3}\)
\(V=\dfrac{1}{3}SH.S_{ABC}=\dfrac{1}{3}.\dfrac{a\sqrt{33}}{3}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^3\sqrt{11}}{12}\)
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có SA vuông góc với đáy. Tính thể tích khối chóp SABC biết: a. Tam giác ABC đều cạnh a, góc giữa SB và đáy là 30°. b. Tam giác ABC vuông tại A, AB=a, SA=5a; góc giữa SC và đáy là 60°
Cho hình chóp SABCD có SA vuông góc với đáy. Tính thể tích khối chóp SABC biết: a. Tam giác ABC đều cạnh a, góc giữa SB và đáy là 30°. b. Tam giác ABC vuông tại A, AB=a, SA=5a; góc giữa SC và đáy là 60°
Cho hình chóp tam giác S.ABC có SA⊥(ABC), đáy ABC là tam giác đều cạnh a, cạnh bên SA a. Gọi M là trung điểm cạnh SB. Tính góc giữa hai đường thẳng SA và CM A.
90
0
B.
45
0
C.
60
0
D.
30
0
Đọc tiếp
Cho hình chóp tam giác S.ABC có SA⊥(ABC), đáy ABC là tam giác đều cạnh a, cạnh bên SA = a. Gọi M là trung điểm cạnh SB. Tính góc giữa hai đường thẳng SA và CM
A. 90 0
B. 45 0
C. 60 0
D. 30 0
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a.
S
A
⊥
A
B
C
và
S
A
a
3
. Thể tích khối chóp SABC là A.
3
a
3
6
B.
a
3
4
C....
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a. S A ⊥ A B C và S A = a 3 . Thể tích khối chóp SABC là
A. 3 a 3 6
B. a 3 4
C. 3 a 3 8
D. 3 a 3 4
Đáp án là B.
V S . A B C = 1 3 S A . S Δ A B C = 1 3 . a 3 . a 2 3 4 = a 3 4 .
Đúng 0
Bình luận (0)
Cho hình tứ diện SABC có đáy ABC là tam giác vuông tại B, có AB = a, BC =a\(\sqrt{5}\), SA vuông góc với (ABC), SA = a\(\sqrt{6}\)
a) Tính (SB;(ABC))
b) Tính (SA;(SBC))
a: (SB;(ABC))=(SB;BA)=góc SBA
\(\tan SBA=\dfrac{SA}{AB}=\sqrt{6}\)
=>góc SBA=68 độ
b: (SA;(SBC))=(SA;SB)=góc ASB
tan ASB=AB/SA=1/căn 6
=>góc ASB=22 độ
Đúng 0
Bình luận (0)
Cho hình chóp SABC , đáy ABC là tam giác vuông cân AB=AC=a, SC⊥(ABC), SC=a, Mặt phẳng qua C vuông góc với SB cắt SA,SB tại E và F. Tính VSCEF.
cho hình chóp sabc đáy tam giác abc đều cạnh a sa vuông góc với đáy
Sa=2a tính VSabc
cho (Sc với ABC bằng 30 độ tính thể tích SABC
Cho h/c SABC có đáy là tam giác vuông tại A, SA⊥(ABC)
cm: AC⊥SB
ΔABC vuông tại A nên AC\(\perp\)AB
AC\(\perp\)AB
AC\(\perp\)SA
AB,SA cùng thuộc mp(SAB)
Do đó: AC\(\perp\)(SAB)
=>AC\(\perp\)SB
Đúng 1
Bình luận (0)