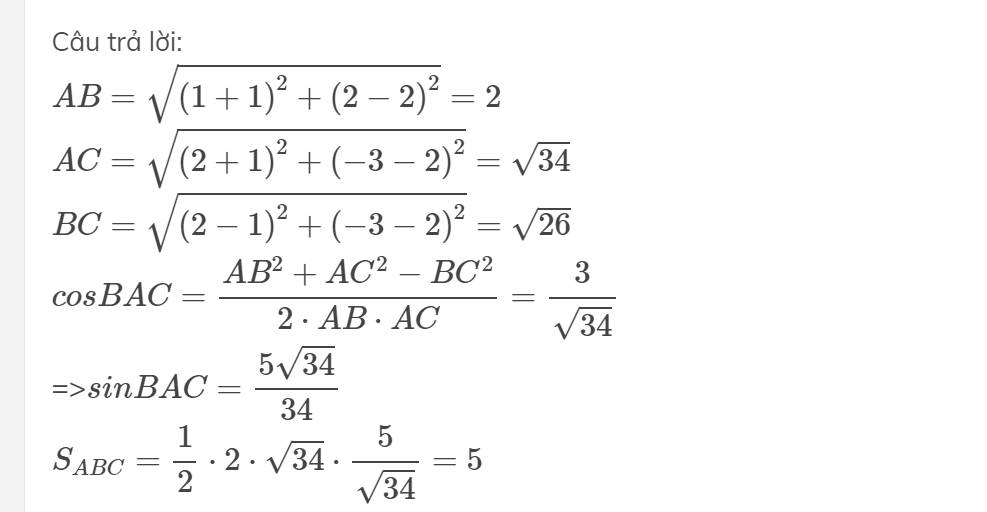trong mp với toạ đo oxy, cho tam giác ABC biết A(2;3),B(1;-2) C(0;6). viết pt các đt đi qua A lần lượt ss và vuông góc với đt BC. viết pt đường tròn có đường kính BC. Tính khoảng cách từ A đến đường thẳng BC

Những câu hỏi liên quan
Tìm toạ độ hình chiếu trọng tâm tam giác ABC trên mp oxy biết A(3,1,-2),B(1,1,4),C(2,-14,1)
Giúp em với ạ em cảm ơn!
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(6;-1) B(-1;2) C(2;5)
a) tính độ dài 3 cạnh vf số đo 3 góc của tam giác ABC
b)Tính chu vi và diện tích của tam giác ABC
c) Tìm toạ độ trực tâm , trọng tâm tam giác ABC.
Gợi ý thôi nhé.
a) Có \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\left(-1\right)-6\right)^2+\left(2-\left(-1\right)\right)^2}=\sqrt{58}\)
Tương tự như vậy, ta tính được AC, BC.
Tính góc: Dùng \(\cos A=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}\)
b) Chu vi thì bạn lấy 3 cạnh cộng lại.
Diện tích: Dùng \(S_{ABC}=\dfrac{1}{2}AB.AC.\sin A\)
c) Gọi \(H\left(x_H,y_H\right)\) là trực tâm thì \(\left\{{}\begin{matrix}AH\perp BC\\BH\perp AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{BH}.\overrightarrow{AC}=0\end{matrix}\right.\)
Sau đó dùng: \(\overrightarrow{u}\left(x_1,y_1\right);\overrightarrow{v}\left(x_2,y_2\right)\) thì \(\overrightarrow{u}.\overrightarrow{v}=x_1x_2+y_1y_2\) để lập hệ phương trình tìm \(x_H,y_H\)
Trọng tâm: Gọi \(G\left(x_G,y_G\right)\) là trọng tâm và M là trung điểm BC. Dùng \(\left\{{}\begin{matrix}x_M=\dfrac{x_B+x_C}{2}\\y_M=\dfrac{y_B+y_C}{2}\end{matrix}\right.\) để tìm tọa độ M.
Dùng \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\) để lập hpt tìm tọa độ G.
Đúng 1
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(6,0); B(3,1); C(-1,-1).Tính số đo góc B của tam giác đã cho
\(\left\{{}\begin{matrix}\overrightarrow{BA}=\left(3;-1\right)\\\overrightarrow{BC}=\left(-4;-2\right)\end{matrix}\right.\)
\(\Rightarrow cos\widehat{ABC}=cos\left(\overrightarrow{BA};\overrightarrow{BC}\right)=\dfrac{3.\left(-4\right)+1.2}{\sqrt{3^2+1^2}.\sqrt{\left(-4\right)^2+\left(-2\right)^2}}=-\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{ABC}=135^0\)
Đúng 0
Bình luận (0)
Trong mp toạ đọ Oxy, cho ∆ ABC biết A(-1,2), B(1,2), C(2,-3). Tính diện tích ∆ AbC
Trong mp toạ đọ Oxy, cho ∆ ABC biết A(-1,2), B(1,2), C(2,-3). Tính diện tích ∆ AbC
\(AB=\sqrt{\left(1+1\right)^2+\left(2-2\right)^2}=2\)
\(AC=\sqrt{\left(2+1\right)^2+\left(-3-2\right)^2}=\sqrt{34}\)
\(BC=\sqrt{\left(2-1\right)^2+\left(-3-2\right)^2}=\sqrt{26}\)
\(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{3}{\sqrt{34}}\)
=>\(sinBAC=\dfrac{5\sqrt{34}}{34}\)
\(S_{ABC}=\dfrac{1}{2}\cdot2\cdot\sqrt{34}\cdot\dfrac{5}{\sqrt{34}}=5\)
Đúng 1
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có A(2;4), B(-1;1), C(-8; 2).
a) Tính số đo góc ABC (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).
b) Tính chu vi của tam giác ABC.
c) Tìm toạ độ điểm M trên đường thẳng BC sao cho diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM.
a) Ta có: \(\overrightarrow {BC} = \left( { - 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right)\)
\(\cos \widehat {ABC} = \left( {\overrightarrow {BC} ,\overrightarrow {BA} } \right) = \frac{{\left( { - 7} \right).3 + 1.3}}{{\sqrt {{{\left( { - 7} \right)}^2} + {1^2}} .\sqrt {{3^2} + {3^2}} }} = - \frac{3}{5} \Rightarrow \widehat {ABC} \approx {126^o}\)
b) Ta có: \(\overrightarrow {BC} = \left( { - 7;1} \right),\overrightarrow {BA} = \left( {3;3} \right),\overrightarrow {AC} = \left( { - 10; - 2} \right)\)
Suy ra: \(\begin{array}{l}AB = \left| {\overrightarrow {BA} } \right| = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \\AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{{\left( { - 10} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt {104} \\BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{{\left( { - 7} \right)}^2} + {1^2}} = \sqrt {50} \end{array}\)
Vậy chu vi tam giác ABC là: \({P_{ABC}} = 2\sqrt {26} + 8\sqrt 2 \)
c) Để diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM thì M phải là trung điểm BC.
Vậy tọa độ điểm M là: \(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = \frac{{ - 9}}{2}\\\frac{{{y_B} + {y_C}}}{2} = \frac{3}{2}\end{array} \right.\). Vậy \(M\left( {\frac{{ - 9}}{2};\frac{3}{2}} \right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy cho tam giác ABC nội tiếp đường tròn tâm I và D là chân đường phân giác trong đỉnh A của tam giác ABC biết toạ độ các đieemr A(2;6) I(-1/2;1) D(2;-3/2) biết phương trình tổng quát của đường thẳng BC
Trong mp toạ độ oxy, cho tam giác ABC vuông tại A, BC có pt là y=0, M là trung điểm cạnh BC, điểm E thuộc đoạn MC. Gọi O(2;1/2) và I(7;8) lần lượt là tâm đường tròn ngoịa tiếp tam giác ABE và ACE. Tìm toạ độ E,M biết rằng hoành độ điểm E lớn hơn hoành độ điểm M
Trong mp toạ đọ Oxy, cho ∆ ABC biết A(-1,2), B(1,2), C(2,-3). Lập pt đường tròn (T) ngoại tiếp ∆ABC. Tìm toạ độ tâm (I) của đtron (T)
\(PT\left(T\right)\) có dạng \(x^2+y^2-2ax-2by+c=0\)
\(\left\{{}\begin{matrix}A\left(-1;2\right)\in\left(T\right)\\B\left(1;2\right)\in\left(T\right)\\C\left(2;-3\right)\in\left(T\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(-1\right)^2+2^2+2a-4b+c=0\\1^2+2^2-2a-4b+c=0\\2^2+\left(-3\right)^2-4a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a-4b+c=-5\\-2a-4b+c=-5\\-4a+6b+c=-13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-\dfrac{4}{5}\\c=-\dfrac{41}{5}\end{matrix}\right.\)
\(\Rightarrow\)Tâm \(I\left(0;-\dfrac{4}{5}\right)\)
Đúng 1
Bình luận (0)