Viết phương trình tham số của các đường thẳng sau :
a) 4x+y-5=0
b) -2x+y+4=0
c) x-5=0
d)y-7=0
Câu 1: Giải phương trình và hệ phương trình
a) \(\sqrt{4x^2-4x+9}=3\)
b) \(\left\{{}\begin{matrix}3x-y=5\\2y-x=0\end{matrix}\right.\)
Câu 2:
a) Cho hai đường thẳng (d\(_1\)): y = 2x - 5 và (d\(_2\)): y = 4x - m (m là tham số). Tìm tất cả các giá trị của tham số m để (d\(_1\)) và (d\(_2\)) cắt nhau tại một điểm trên trục hoành Ox
b) Rút gọn biểu thức: \(P=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{2x}{9-x}\right):\left(\dfrac{\sqrt{x}-1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\) với x > 0, x \(\ne\) 9, x \(\ne\) 25
a) \(\sqrt{4x^2-4x+9}=3\)
Vì \(4x^2-4x+9=\left(2x-1\right)^2+8>0\)( Với mọi x )
Nên \(\sqrt{4x^2-4x+9}=3\)
⇔\(4x^2-4x+9=9\)
⇔\(4x^2-4x=0\)
⇔\(4x\left(x-1\right)=0\)
⇔\(\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)là nghiệm
Câu 26. Cho hai đường tròn (C):(x-2)^ 2 +(y-2)^ 2 =9;(C' ):x^ 2 +y^ 2 +4x-8y+11=0 ,biết (C) và (C') đối xứng nhau qua đường thẳng (a) .Phương trình của (a) là : A. 2x + 2y - 4 = 0 B.2x-y+3=0 . C. x + y - 4 = 0 . D. 2x + 2y = 0 .
(3)
a) gpt: \(\sqrt{2x-3}-x+3=0\)
b) tìm các giá trị của tham số m để pt \(\sqrt{2x^2+mx-3}=x+1\) có 2 nghiệm phân biệt.
(4) trong mặt phẳng tọa độ Oxy, cho điểm I (1; -2) và 2 đg thẳng d1: 3x+y+5=0, d2: 3x+y+1=0.
a) viết phương trình đg thẳng d vuông góc với đg thẳng d1 và đi qua gốc tọa độ
b) viết pt đg thẳng đi qua 1 và cắt d1, d2 lần lượt tại A và B sao cho AB= \(2\sqrt{2}\)
giúp mk vs ạ mk cần gấp
(3):
a: =>căn 2x-3=x-3
=>x>=3 và x^2-6x+9=2x-3
=>x>=3 và x^2-8x+12=0
=>x=6
b: =>x>=-1 và 2x^2+mx-3=x^2+2x+1
=>x>=-1 và x^2+(m-2)x-4=0
=>với mọi m thì pt luôn có hai nghiệm phân biệt lớn hơn -1 vì a*c<0
Trong mặt phẳng Oxy cho A (4;1), B (-2;3), C (5;-1). a) Viết phương trình tham số và trình tổng quát của đường thẳng đi qua hai điểm A,C b) Viết phương trình tham số và trình tổng quát của đường thẳng A và vuông góc với B,C c) Viết phương trình tham số và trình tổng quát của đường thẳng qua A và song song với đường thẳng d : 2x - y + 3 = 0
Phương trình nào sau đây là phương trình tham số của đường thẳng?
A. \(2x - y + 1 = 0\)
B. \(\left\{ \begin{array}{l}x = 2t\\y = t\end{array} \right.\)
C. \({x^2} + {y^2} = 1\)
D. \(y = 2x + 3\)
Cho mặt phẳng α : 4 x + y + 2 z + 1 = 0 và β : 2 x - 2 y + z + 3 = 0 . Viết phương trình tham số của đường thẳng d là giao của (α) và (β).
A. x = t y = 1 - t z = - 1 - 2 t
B. x = t y = 1 z = - 1 - 2 t
C. x = - t y = 1 z = - 1 - 2 t
D. x = - t y = 1 + t z = - 1 - 2 t
Cho mặt phẳng ( α ) : 4 x + y + 2 z + 1 = 0 và ( β ) : 2 x - 2 y + z - 3 = 0 . Viết phương trình tham số của đường thẳng d là giao của α và β
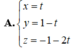
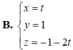
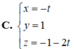
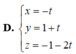
30. Viết pt tham số của đg thẳng đi qua 2 điểm A ( 3;-7) và B(1;-7)
A. x =t ; y =-7
B. x=t ; y =7
C. x=t ; y = -7-t
D. x = 3-7t; y = 1-7t
31. Trong mặt phẳng toạ độ Oxy , viết pt tổng quát của đg trung trực của đoạn thẳng AB với A(2;3) và B(-4;-1).
A. 3x - 2y +5 =0
B. 3x - 2y -5=0
C. 3x +2y +1 =0
D. 3x +2y -1=0
32. Trong mặt phẳng toạ độ Oxy , viết pt tổng quát của đg thẳng đi qua giao điểm của d1 : 3x - 5y +2=0 và d2 : 5x -2y +4=0 đồng thời sống song với đg thẳng d3 : 2x - y +4=0
A. 2x - y + 30/19 =0
B. 2x -y - 30/19=0
C. x +2y + 30/19=0
D. x +2y - 30/19=0
33. Trong mặt phẳng toạ độ Oxy , cho tg ABC với A(-1;2), B(1;1) , C(2;-1) . Viết pt tổng quát đg cao AH của tg ABC.
A. AH : x -2y +3=0
B. AH: 2x +y =0
C. AH : x -2y +5=0
D. AH: 2x - y +4 =0
34. Cho tg ABC có toạ độ các đỉnh là A(-1;1) và B(4;7) , C( 3;-2), M là trung điểm của đoạn thẳng AB. Viêt pt tham số của đg thẳng CM.
A. x = 3+t ; y = -2-4t
B. x = 3+t ;y = -2 + 4t
C. x = 3-t ; y = 4+2t
D. x = 3+3t ; y = -2+4t
Câu 32:
Gọi M là giao điểm d1;d2 thì tọa độ M là nghiệm của hệ:
\(\left\{{}\begin{matrix}3x-5y+2=0\\5x-2y+4=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{16}{19};-\frac{2}{19}\right)\)
Do d song song d3 nên d nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình d:
\(2\left(x+\frac{16}{19}\right)-1\left(y+\frac{2}{19}\right)=0\Leftrightarrow2x-y+\frac{30}{19}=0\)
Câu 33:
\(\overrightarrow{BC}=\left(1;-2\right)\)
Do AH vuông góc BC nên AH nhận \(\left(1;-2\right)\) là 1 vtpt
Phương trình AH:
\(1\left(x+1\right)-2\left(y-2\right)=0\Leftrightarrow x-2y+5=0\)
Câu 34:
Tọa độ M là: \(M\left(\frac{3}{2};4\right)\)
\(\overrightarrow{CM}=\left(-\frac{3}{2};6\right)=-\frac{3}{2}\left(1;-4\right)\)
Phương trình tham số CM: \(\left\{{}\begin{matrix}x=3+t\\y=-2-4t\end{matrix}\right.\)
Câu 30:
\(\overrightarrow{AB}=\left(-2;0\right)=-2\left(1;0\right)\) nên đường thẳng AB nhận \(\left(1;0\right)\) là 1 vtcp
Phương trình AB: \(\left\{{}\begin{matrix}x=1+t\\y=-7\end{matrix}\right.\)
Cả 4 đáp án đều ko chính xác
Câu 31:
Gọi M là trung điểm AB \(\Rightarrow M\left(-1;1\right)\)
\(\overrightarrow{AB}=\left(-6;-4\right)=-2\left(3;2\right)\Rightarrow\) đường trung trực AB nhận \(\left(3;2\right)\) là 1vtpt
Phương trình:
\(3\left(x+1\right)+2\left(y-1\right)=0\Leftrightarrow3x+2y+1=0\)