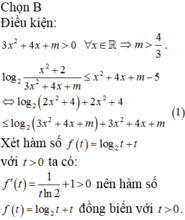2: \(-4x^2+5x-2\)

\(=-4\left(x^2-\dfrac{5}{4}x+\dfrac{1}{2}\right)\)

\(=-4\left(x^2-2\cdot x\cdot\dfrac{5}{8}+\dfrac{25}{64}+\dfrac{7}{64}\right)\)

\(=-4\left(x-\dfrac{5}{8}\right)^2-\dfrac{7}{16}< =-\dfrac{7}{16}< 0\forall x\)

Sửa đề:\(f\left(x\right)=\dfrac{-x^2+4\left(m+1\right)x+1-4m^2}{-4x^2+5x-2}\)

Để f(x)>0 với mọi x thì \(\dfrac{-x^2+4\left(m+1\right)x+1-4m^2}{-4x^2+5x-2}>0\forall x\)

=>\(-x^2+4\left(m+1\right)x+1-4m^2< 0\forall x\)(1)

\(\text{Δ}=\left[\left(4m+4\right)\right]^2-4\cdot\left(-1\right)\left(1-4m^2\right)\)

\(=16m^2+32m+16+4\left(1-4m^2\right)\)

\(=32m+20\)

Để BĐT(1) luôn đúng với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< 0\\a< 0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}32m+20< 0\\-1< 0\left(đúng\right)\end{matrix}\right.\)

=>32m+20<0

=>32m<-20

=>\(m< -\dfrac{5}{8}\)

\(\Leftrightarrow\) Với mọi \(x>0\) ta luôn có:

\(x^3-x^2-2x+m\left(x+1\right)\ge0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2-2x\right)+m\left(x+1\right)\ge0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2-2x+m\right)\ge0\)

\(\Leftrightarrow x^2-2x+m\ge0\) (do \(x+1>0\) ; \(\forall x>0\))

\(\Leftrightarrow m\ge-x^2+2x\)

\(\Leftrightarrow m\ge\max\limits_{x>0}\left(-x^2+2x\right)=1\)

\(\Rightarrow m=\left\{1;2;3;4;...;10\right\}\)

Chọn D

ĐKXĐ: \(x\ge0\)

- Với \(x=0\) ko phải là nghiệm

- Với \(x>0\) chia 2 vế cho \(x\) ta được:

\(\dfrac{x^2+4}{x}+2-m=4\sqrt{\dfrac{x^2+4}{x}}\)

Đặt \(\sqrt{\dfrac{x^2+4}{x}}=t\ge2\)

\(\Rightarrow t^2-4t+2=m\)

Xét hàm \(f\left(t\right)=t^2-4t+2\) với \(t\ge2\)

\(\Rightarrow f\left(t\right)\ge f\left(2\right)=-2\Rightarrow m\ge-2\)

Có \(2018-\left(-2\right)+1=2021\) giá trị nguyên của m

\(x^2-x+m\le0\)

\(\Leftrightarrow m\le f\left(x\right)=-x^2+x\)

Bảng biến thiên:

Yêu cầu bài toán thỏa mãn khi \(m>maxf\left(x\right)=f\left(\dfrac{1}{2}\right)=\dfrac{1}{4}\)

đáp án :m>1/4

Đặt \(x^2+4x+3=t\left(t\ge-1\right)\)

\(\left(x^2+4x+3\right)\left(x^2+4x+6\right)\ge m,\forall x\in R\)

\(\Leftrightarrow\left(x^2+4x+3\right)^2+3\left(x^2+4x+3\right)\ge m,\forall x\in R\)

\(\Leftrightarrow m\le f\left(t\right)=t^2+3t,\forall x\in R\)

Yêu cầu bài toán thỏa mãn khi:

\(m\le minf\left(t\right)=-2\)

Đáp án D.

Ta có:

P T ⇔ m 9 4 x − 2 m + 1 6 4 x + m ≤ 0 ⇔ m 3 2 2 x − 2 m + 1 3 2 x + m ≤ 0

Đặt t = 3 2 x ;  do x ∈ 0 ; 1 ⇒ t ∈ 1 ; 3 2 .  Khi đó PT trở thành: m t 2 − 2 m + 1 t + m ≤ 0 ⇔ m t 2 − 2 t + 1 ≤ t

Rõ ràng t = 1 là nghiệm của BPT đã cho.

Với t ∈ 1 ; 3 2 ⇒ m ≤ t t − 1 2 = f t ,  xét f x  với t ∈ 1 ; 3 2  ta có:

f ' t = t − 1 − 2 t t − 1 3 = − t − 1 t − 1 2 < 0 ∀ t ∈ 1 ; 3 2

do đó f t   nghịch biến trên 1 ; 2 3 .

Do đó BPT nghiệm đúng vơi ∀ t ∈ 1 ; 3 2 ⇔ m ≤ M i n 1 ; 3 2 f t = f 3 2 = 6

Vậy có 6 giá trị nguyên dương của m thỏa mãn.