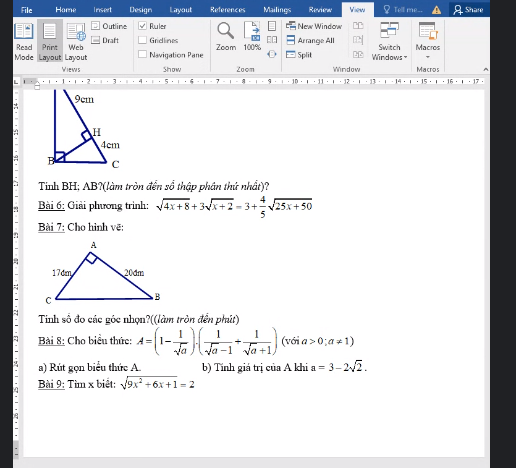
 giúp em bài 8 với 9 ạ :<
giúp em bài 8 với 9 ạ :<

Những câu hỏi liên quan
giúp em bài 8 bài 9 với ạ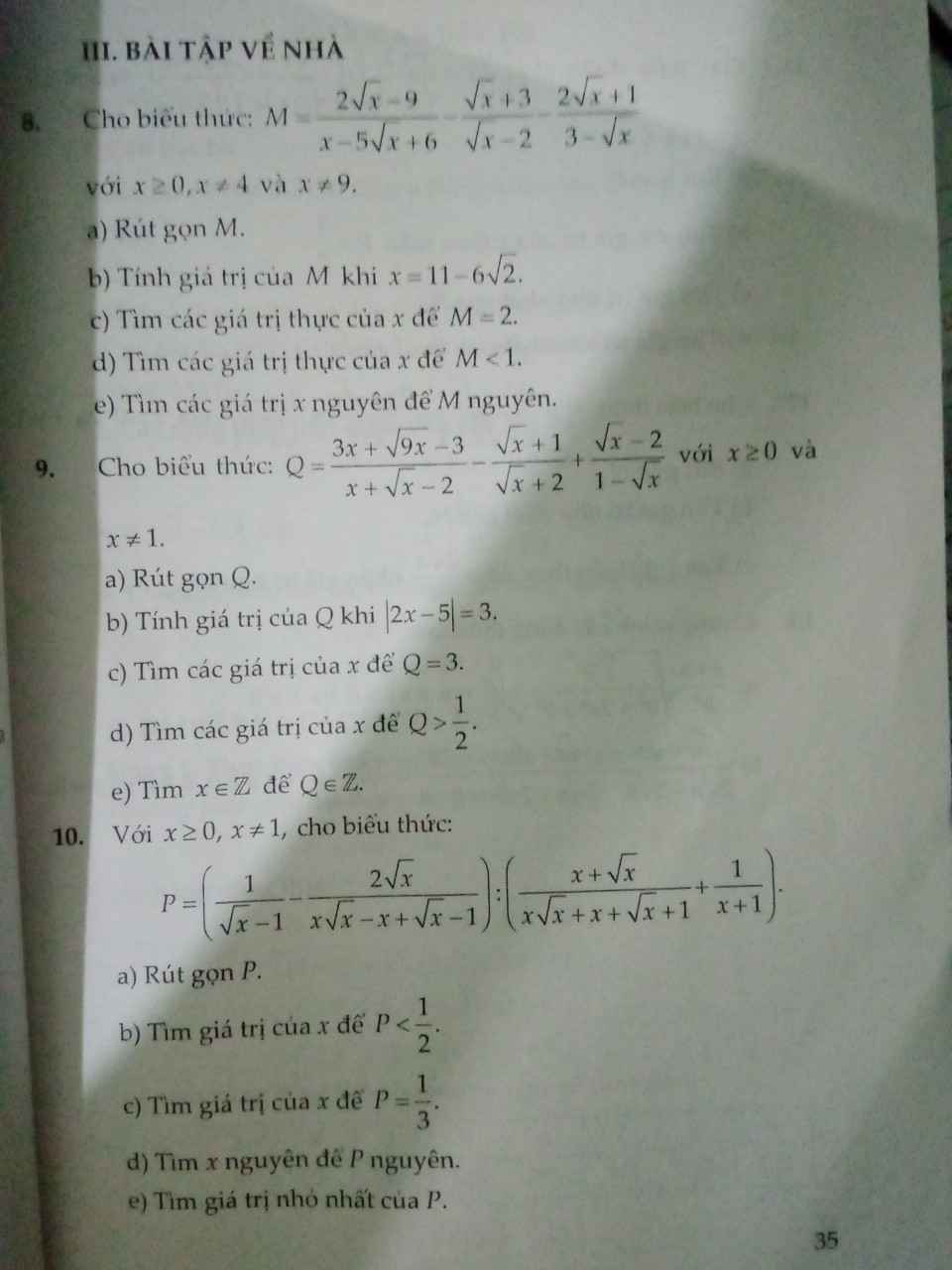
Bài 8:
a: Ta có: \(M=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b: Thay \(x=11-6\sqrt{2}\) vào M, ta được:
\(M=\dfrac{3-\sqrt{2}+1}{3-\sqrt{2}-3}=\dfrac{4-\sqrt{2}}{-\sqrt{2}}=-2\sqrt{2}+1\)
Đúng 0
Bình luận (0)
Bài 8:
a) \(M=\dfrac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
b) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{\sqrt{11-6\sqrt{2}}+1}{\sqrt{11-6\sqrt{2}}-3}=\dfrac{\sqrt{\left(3-\sqrt{2}\right)^2}+1}{\sqrt{\left(3-\sqrt{2}\right)^2}-3}=\dfrac{4-\sqrt{2}}{-\sqrt{2}}=1-2\sqrt{2}\)
c) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=3\)
\(\Leftrightarrow3\sqrt{x}-9=\sqrt{x}+1\Leftrightarrow2\sqrt{x}=10\Leftrightarrow\sqrt{x}=5\Leftrightarrow x=25\left(tm\right)\)
d) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}< 1\)
\(\Leftrightarrow\sqrt{x}+1< \sqrt{x}-3\Leftrightarrow1< -3\left(VLý\right)\)
Vậy \(S=\varnothing\)
e) \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\in Z\)
\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\)
Kết hợp đk:
\(\Rightarrow x\in\left\{1;16;25;49\right\}\)
Đúng 1
Bình luận (0)
Giúp em bài 8 và 9 với ạ
Bài 10:
a: =254-254+135=135
Đúng 0
Bình luận (0)
Giúp em bài 8 9 10 11 12 với ạ
Giúp em bài 6 với 9 với ạ. Vẽ hình giúp en nx. Em cảm ơn ạ. 
Bài 10:
a: \(\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OA}\)
\(=\overrightarrow{AO}+\overrightarrow{OA}=\overrightarrow{0}\)
b: \(\overrightarrow{OA}+\overrightarrow{BC}+\overrightarrow{DO}+\overrightarrow{CD}\)
\(=\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{BD}\)
\(=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BA}\)
Đúng 0
Bình luận (0)
 Giải giúp em bài 8 9 10 đi ạ
Giải giúp em bài 8 9 10 đi ạ
Bài 8.9.10 của câu 14 hay 15 bạn?
Đúng 1
Bình luận (0)
Câu 15:
1: Ta có: \(\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{1+\sqrt{2}}\)
\(=\dfrac{1+\sqrt{2}-1+\sqrt{2}}{\left(1-\sqrt{2}\right)\left(1+\sqrt{2}\right)}\)
\(=-2\sqrt{2}\)
2: Ta có: \(\dfrac{1}{\sqrt{5}+1}+\dfrac{1}{\sqrt{5}-1}\)
\(=\dfrac{\sqrt{5}-1+\sqrt{5}+1}{\left(\sqrt{5}+1\right)\left(\sqrt{5}-1\right)}\)
\(=\dfrac{2\sqrt{5}}{4}=\dfrac{\sqrt{5}}{2}\)
Đúng 1
Bình luận (0)
Câu 14:
8: Ta có: \(\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{x-2}{x-3\sqrt{x}+2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}-\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}+\dfrac{x-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-4\sqrt{x}+3-2x+4\sqrt{x}+\sqrt{x}-2+x-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{1}{\sqrt{x}-2}\)
9: Ta có: \(\dfrac{3\sqrt{x}+2}{2\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+4}-\dfrac{x-6\sqrt{x}+5}{2x-7\sqrt{x}-4}\)
\(=\dfrac{\left(3\sqrt{x}+2\right)\left(\sqrt{x}+4\right)}{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+4\right)}+\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+4\right)}-\dfrac{x-6\sqrt{x}+5}{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+4\right)}\)
\(=\dfrac{3x+12\sqrt{x}+2\sqrt{x}+8+2x-\sqrt{x}-2\sqrt{x}+1-x+6\sqrt{x}-5}{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+4\right)}\)
\(=\dfrac{4x+20\sqrt{x}+4}{\left(2\sqrt{x}-1\right)\left(\sqrt{x}+4\right)}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp em bài toán lớp 9 với ạ .Chiều e kiểm tra rồi .GIÚP EM VỚI .EM CẢM ƠN NHIỀU Ạ !!!
b: \(BC=\sqrt{89}\left(cm\right)\)
\(\sin\widehat{B}=\dfrac{5\sqrt{89}}{89}\)
\(\Leftrightarrow\widehat{B}\simeq32^0\)
\(\widehat{C}=58^0\)
Đúng 0
Bình luận (0)
Giúp em làm cậu 8 với 9 với ạ em đang cần gấp ạ

Mn ưi giúp em bài này với![]()
Câu 8 và câu 9 của chủ đề 2 ạ
Em cám ơn mn nhìu ạ<3
8) \(\dfrac{x+7}{3}+\dfrac{x+5}{4}=\dfrac{x+3}{5}+\dfrac{x+1}{6}\)
\(\Rightarrow\dfrac{x+7}{3}+\dfrac{x+5}{4}-\dfrac{x+3}{5}-\dfrac{x+1}{6}=0\)
\(\Rightarrow\dfrac{x+7}{3}+2+\dfrac{x+5}{4}+2-\dfrac{x+3}{5}-2-\dfrac{x+1}{6}-2=0+2+2-2-2\)
\(\Rightarrow\left(\dfrac{x+7}{3}+2\right)+\left(\dfrac{x+5}{4}+2\right)-\left(\dfrac{x+3}{5}+2\right)-\left(\dfrac{x+1}{6}+2\right)=0\)
\(\Rightarrow\left(\dfrac{x+7}{3}+\dfrac{6}{3}\right)+\left(\dfrac{x+5}{4}+\dfrac{8}{4}\right)-\left(\dfrac{x+3}{5}+\dfrac{10}{5}\right)-\left(\dfrac{x+1}{6}+\dfrac{12}{2}\right)=0\)
\(\Rightarrow\left(x+13\right)\left(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}-\dfrac{1}{6}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+13=0\\\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\end{matrix}\right.\)
\(x+13=0\)
\(\Rightarrow x=-13\)
\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}=0\)
\(\dfrac{13}{60}=0\) (vô lí)
Vậy \(x=-13\)
9) Bạn chuyển vế rồi cộng 3 vào từng mỗi số
Đúng 4
Bình luận (1)
8) Ta có: \(\dfrac{x+7}{3}+\dfrac{x+5}{4}=\dfrac{x+3}{5}+\dfrac{x+1}{6}\)
\(\Leftrightarrow\dfrac{x+13}{6}+\dfrac{x+13}{4}=\dfrac{x+13}{5}+\dfrac{x+13}{6}\)
Suy ra: x+13=0
hay x=-13
Đúng 1
Bình luận (0)
9) Ta có: \(\dfrac{x+19}{3}+\dfrac{x+13}{5}=\dfrac{x+7}{7}+\dfrac{x+1}{9}\)
\(\Leftrightarrow\dfrac{x+28}{3}+\dfrac{x+28}{5}-\dfrac{x+28}{7}-\dfrac{x+28}{9}=0\)
Suy ra: x+28=0
hay x=-28
Đúng 0
Bình luận (0)
Anh chị ơi giúp em bài kiểm tra lớp 9 với ạ .em còn câu 5 6 7 anh chị giúp em với .Em cảm ơn rất nhiều ạ!!!!!!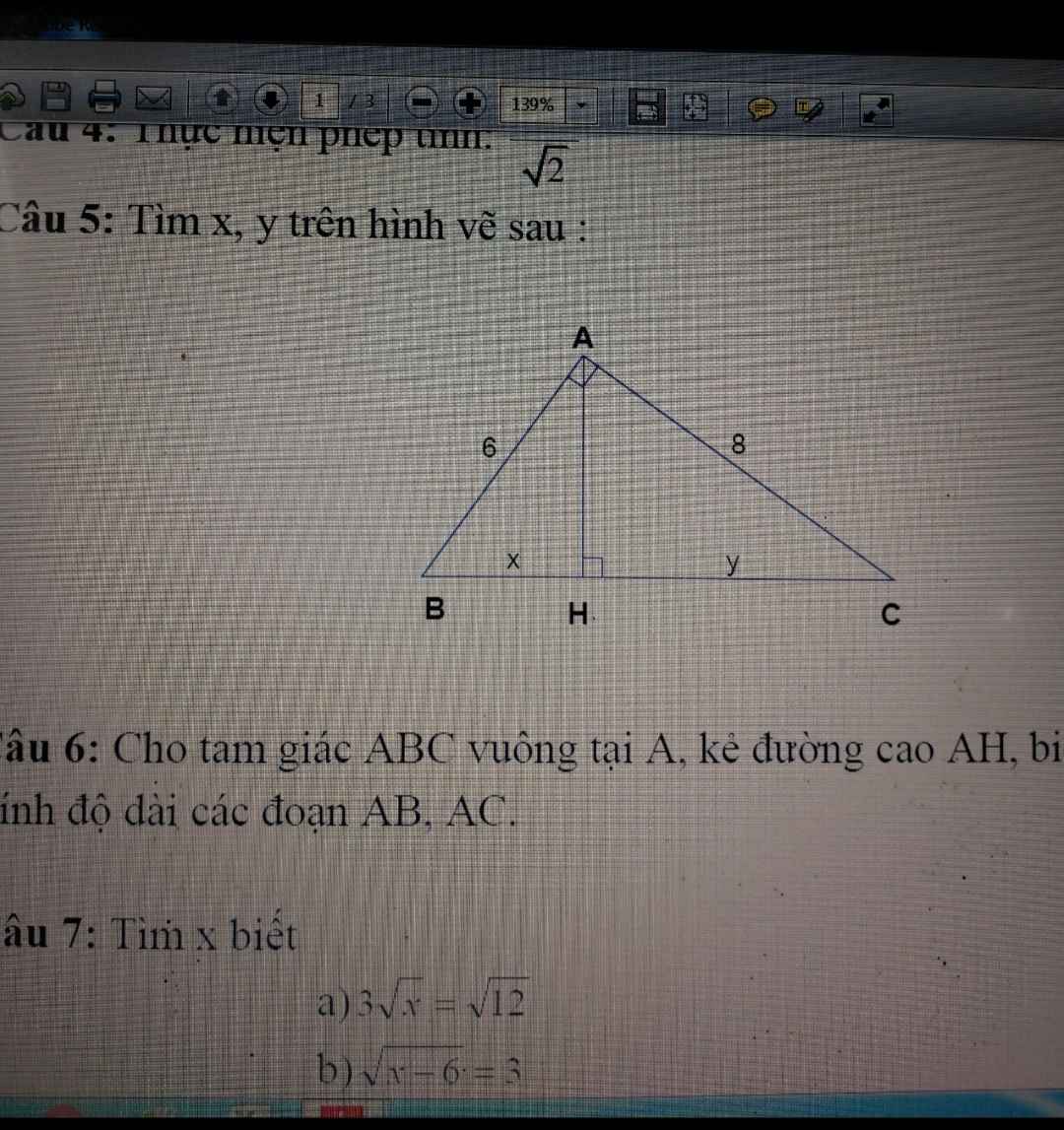
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)
Đúng 0
Bình luận (0)
Câu 5:
Áp dụng định lý Pi-ta-go ta có:
\(AB^2+AC^2=BC^2\\ \Rightarrow BC=\sqrt{6^2+8^2}\\ \Rightarrow BC=10\)
Áp dụng HTL ta có: \(x.BC=AB^2\Rightarrow x.10=6^2\Rightarrow x=3,6\)
Áp dụng HTL ta có: \(x.BC=AC^2\Rightarrow x.10=8^2\Rightarrow x=6,4\)
Đúng 0
Bình luận (0)


















