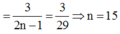Cho đa giác đều \(A_1A_2...A_{2n}\) nội tiếp đường tròn \(\left(O,R\right)\) . Biết rằng số tam giác có các đỉnh là 3 trong 2n điểm \(A_1,A_2,...,A_{2n}\) nhiều gấp 20 lần số hình chữ nhật có các đỉnh là 4 trong 2n điểm \(A_1,A_2,...,A_{2n}\) . Tìm n

Những câu hỏi liên quan
Cho đa giác đều \(A_1A_2.....A_n,\) (\(n\ge2\), n nguyên) nội tiếp đường tròn O. Biết rằng số tam giác có 3 đỉnh trong 2 n điểm \(A_1,A_2,....,.A_{2n}\) gấp 20 lần số hình chữ nhật có 4 đỉnh trong 2n điểm \(A_1A_2.....A_n\). Tìm n
Số tam giác là \(C_{2n}^3\). Một đa giác đều 2n đỉnh thì có n đường chéo xuyên tâm. Cứ 2 đường chéo xuyên tâm thì có một hình chữ nhật theo yêu cầu. Vậy số hình chữ nhật là \(C_n^2\).
Theo bài ta có phương trình :
\(C_{2n}^3=20C_n^2,\left(n\ge2\right)\)
\(\Leftrightarrow\frac{\left(2n\right)!}{\left(2n-3\right)!3!}=20\frac{n!}{\left(n-2\right)!2!}\)
\(\Leftrightarrow\frac{\left(2n-2\right)\left(2n-1\right)2n}{3}=20\left(n-1\right)n\)
\(\Leftrightarrow2\left(n-1\right)\left(2n-1\right)2n=60\left(n-1\right)n\)
\(\Leftrightarrow2n-1=15\), (do \(n\ge2\))
\(\Leftrightarrow n=18\)
Vậy đa giác đều có 16 cạnh, (thập lục giác đều)
Đúng 0
Bình luận (0)
Cho đa giác đều \(A_1A_2...A_{2n}\left(n\ge2,n\in N\right).\) Biết rằng số vecto khác vecto 0 có điểm đầu và điểm cuối thuộc tập hợp điểm \(\left\{A_1,A_2,...,A_{2n}\right\}\) bằng 9 lần số hình chữ nhật có các đỉnh thuộc tập hợp điểm \(\left\{A_1,A_2,...,A_{2n}\right\}\). Tìm n
Số vecto tạo từ 2n điểm là: \(A_{2n}^2\)
Đa giác đều 2n đỉnh có n đường chéo, cứ 2 đường chéo cho ta 1 hình chữ nhật tương ứng, do đó số hình chữ nhật có đỉnh là đỉnh của đa giác đều là: \(C_n^2\)
\(\Rightarrow A_{2n}^2=9C_n^2\Leftrightarrow\dfrac{\left(2n\right)!}{\left(2n-2\right)!}=\dfrac{9.n!}{2!.\left(n-2\right)!}\)
\(\Leftrightarrow2n\left(2n-1\right)=\dfrac{9n\left(n-1\right)}{2}\)
\(\Leftrightarrow n=5\)
Đúng 2
Bình luận (2)
Cho đa giác đều A1A2…A2n nội tiếp trong đường tròn tâm O. Biết rằng số tam giác có đỉnh là 3 trong 2n điểm A1;A2;…;A2n gấp 20 lần so với số hình chữ nhật có đỉnh là 4 trong 2n điểm A1;A2;…;A2n . Tìm n? A. 3 B. 6 C.8 D.12
Đọc tiếp
Cho đa giác đều A1A2…A2n nội tiếp trong đường tròn tâm O. Biết rằng số tam giác có đỉnh là 3 trong 2n điểm A1;A2;…;A2n gấp 20 lần so với số hình chữ nhật có đỉnh là 4 trong 2n điểm A1;A2;…;A2n . Tìm n?
A. 3
B. 6
C.8
D.12
Số tam giác có các đỉnh là 3 trong 2n điểm A1;A2;…;A2n là: ![]()
Ta thấy ứng với hai đường chéo đi qua tâm O của đa giác A1A2…A2n cho tương ứng một hình chữ nhật có 4 đỉnh là 4 điểm trong 2n điểm A1;A2;…;A2n và ngược lại mỗi hình chữ nhật như vậy sẽ cho tương ứng hai đường chéo đi qua tâm O của đa giác.
Mà số đường chéo đi qua tâm của đa giác là n nên số hình chữ nhật có đỉnh là 4 trong 2n điểm bằng ![]()
Theo giả thiết: ![]()
⇒n=8.
Chọn C
Đúng 0
Bình luận (0)
Cho đa giác đều
A
1
A
2
.
..
A
2
n
n
≥
2
,
n
∈
Z
nội tiếp đường tròn O. Biết rằng số tam giác trong 2n điểm
A
1
,
A...
Đọc tiếp
Cho đa giác đều A 1 A 2 . .. A 2 n n ≥ 2 , n ∈ Z nội tiếp đường tròn O. Biết rằng số tam giác trong 2n điểm A 1 , A 2 , . .. , A 2 n gấp 20 lần số hình chữ nhật có 4 đỉnh trong 2n điểm đó. Tìm n.
A. 12
B. 8
C. 16
D. 10
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O . Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n? A. 20 B. 12 C. 15 D. 10
Đọc tiếp
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O ![]() . Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n?
. Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n?
A. 20
B. 12
C. 15
D. 10
Đáp án C
Phương pháp: Số tam giác vuông bằng số đường kính của đường tròn có đầu mút là 2 đỉnh của đa giác (H) nhân với (2n – 2) tức là số đỉnh còn lại của đa giác.
Cách giải: Số phần tử của không gian mẫu: n Ω = C 2 n 3
Tam giác vuông được chọn là tam giác chứa một cạnh là đường kính của đường tròn tâm O.
Đa giác đều 2n đỉnh chứa 2n đường chéo là đường kính của đường tròn tâm O, mỗi đường kính tạo nên 2n – 2 tam giác vuông.
Do đó số tam giác vuông trong tập S là: ![]()
Xác suất chọn một tam giác vuông trong tập S :
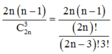
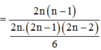
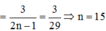
Đúng 0
Bình luận (0)
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O (n
∈
N*, n
≥
2). Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là
3
29
. Tìm n? A. 20 B. 12 C. 15 D. 10
Đọc tiếp
Cho (H) là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O (n ∈ N*, n ≥ 2). Gọi S là tập hợp các tam giác có 3 đỉnh là các đỉnh của đa giác (H). Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn một tam giác vuông trong tập S là 3 29 . Tìm n?
A. 20
B. 12
C. 15
D. 10
Cho H là đa giác đều 2n đỉnh nội tiếp đường tròn tâm O n ∈ N , n ≥ 2 . Gọi S là tập hợp các tam giác có ba đỉnh là các đỉnh của đa giác H . Chọn ngẫu nhiên một tam giác thuộc tập S, biết rằng xác suất chọn được một tam giác vuông trong tập S là 1 3. Tìm n.
Cho một tam giác đều ABC cạnh a. Tam giác {A_1}{B_1}{C_1} có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác {A_2}{B_2}{C_2} có các đỉnh là trung điểm các cạnh của tam giác {A_1}{B_1}{C_1}, ldots , tam giác {A_{n + 1}}{B_{n + 1}}{C_{n + 1}} có các đỉnh là trung điểm các cạnh của tam giác {A_n}{B_n}{C_n}, ldots Gọi {p_1},{p_2}, ldots ,{p_n}, ldots và {S_1},{S_2}, ldots ,{S_n}, ldots theo thứ tự là chu vi và diện tích của các tam giác {A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, ldots ,{A_n}{B_n...
Đọc tiếp
Cho một tam giác đều ABC cạnh \(a\). Tam giác \({A_1}{B_1}{C_1}\) có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác \({A_2}{B_2}{C_2}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_1}{B_1}{C_1}, \ldots \), tam giác \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}\) có các đỉnh là trung điểm các cạnh của tam giác \({A_n}{B_n}{C_n}, \ldots \) Gọi \({p_1},{p_2}, \ldots ,{p_n}, \ldots \) và \({S_1},{S_2}, \ldots ,{S_n}, \ldots \) theo thứ tự là chu vi và diện tích của các tam giác \({A_1}{B_1}{C_1},{A_2}{B_2}{C_2}, \ldots ,{A_n}{B_n}{C_n}, \ldots \).
a) Tìm giới hạn của các dãy số \(\left( {{p_n}} \right)\) và \(\left( {{S_n}} \right)\).
b) Tìm các tổng \({p_1} + {p_2} + \ldots + {p_n} + \ldots \) và \({S_1} + {S_2} + \ldots + {S_n} + \ldots \).
Tham khảo:
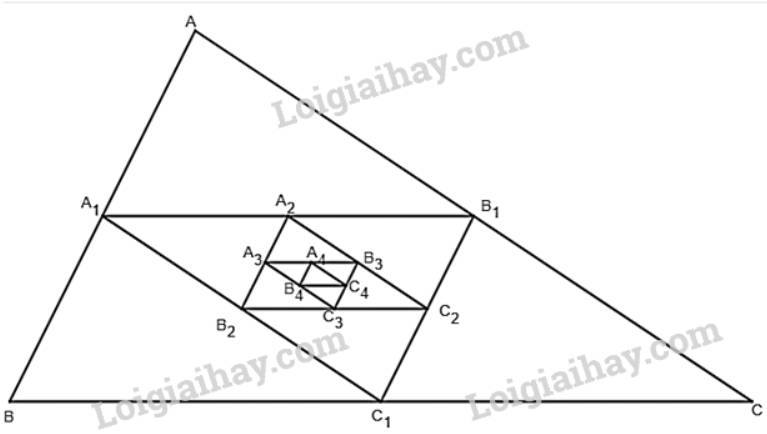
+) \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là dãy số chu vi của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Ta có:
\({{\rm{p}}_2} = {p_{\Delta {A_1}{B_1}{C_1}}} = \frac{a}{2} + \frac{a}{2} + \frac{a}{2} = \frac{1}{2} \cdot (3a) = \frac{1}{2} \cdot {p_1}\)
\(\begin{array}{l}{{\rm{p}}_3} = {p_{\Delta {A_2}{B_2}{C_2}}} = \frac{a}{4} + \frac{a}{4} + \frac{a}{4} = {\left( {\frac{1}{2}} \right)^2} \cdot (3a) = {\left( {\frac{1}{2}} \right)^2} \cdot {p_1}\\ \ldots \\{p_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot {p_1}\\...\end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {p_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{2}} \right)}^{n - 1}} \cdot (3a)} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{2}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } (3a) = 0.3a = 0.\)
+)\(\left( {{{\rm{S}}_n}} \right)\) là dãy số diện tích của các tam giác theo thứ tự \({\rm{ABC}},{{\rm{A}}_1}\;{{\rm{B}}_1}{{\rm{C}}_1}, \ldots \)
Gọi \(h\) là chiều cao của tam giác \({\rm{ABC}}\) và \({\rm{h}} = \frac{{a\sqrt 3 }}{2}\).
Ta có:
\(\begin{array}{l}{{\rm{S}}_3} = {S_{\Delta {A_2}{B_2}{C_2}}} = \frac{1}{2} \cdot \frac{a}{4} \cdot \frac{h}{4} = {\left( {\frac{1}{4}} \right)^2} \cdot \left( {\frac{1}{2}ah} \right) = {\left( {\frac{1}{4}} \right)^2} \cdot {S_1}\\ \ldots \\{S_{\Delta {A_n}{B_n}{C_n}}} = {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot {S_1}\\ \ldots \end{array}\)
\( \Rightarrow \mathop {\lim }\limits_{n \to \infty } {S_n} = \mathop {\lim }\limits_{n \to \infty } \left( {{{\left( {\frac{1}{4}} \right)}^{n - 1}} \cdot {S_1}} \right) = \mathop {\lim }\limits_{n \to \infty } {\left( {\frac{1}{4}} \right)^{n - 1}} \cdot \mathop {\lim }\limits_{n \to \infty } \left( {\frac{1}{2}ah} \right) = 0 \cdot \frac{1}{2}ah = 0\).
b) +) Ta có \(\left( {{{\rm{p}}_{\rm{n}}}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{p}}_1}\) = 3a và công bội \({\rm{q}} = \frac{1}{2}\) thỏa mãn \(|q| < 1\) có tổng:
\({p_1} + {p_2} + \ldots + {p_n} + \ldots = \frac{{3a}}{{1 - \frac{1}{2}}} = 6a\)
+) Ta có \(\left( {{{\rm{S}}_n}} \right)\) là một cấp số nhân lùi vô hạn với số hạng đầu \({{\rm{S}}_1} = \frac{1}{2}ah\) và công bội \(q = \frac{1}{4}\) thỏa mãn \(|q| < 1\) có tổng:
\({S_1} + {S_2} + \ldots + {S_n} + \ldots = \frac{{\frac{1}{2}ah}}{{1 - \frac{1}{4}}} = \frac{2}{3}ah = \frac{2}{3}a.\frac{{a\sqrt 3 }}{2} = \frac{{{a^2}\sqrt 3 }}{3}\)
Đúng 0
Bình luận (0)
Cho đa giác đều A1A2... A2n nội tiếp trong đường tròn tâm O. Hỏi có bao nhiêu tam giác có đỉnh là 3 trong 2N điểm A1; A2;...; A2n A.
C
2
n
3
B.
C
n
3
C.
A
2
n
3
D.
A
n
3
Đọc tiếp
Cho đa giác đều A1A2... A2n nội tiếp trong đường tròn tâm O. Hỏi có bao nhiêu tam giác có đỉnh là 3 trong 2N điểm A1; A2;...; A2n
A. C 2 n 3
B. C n 3
C. A 2 n 3
D. A n 3