cho \(y=ax^2+bx+c=f\left(x\right)\) có đồ thị đi qua \(A\left(1;8\right),Max=9\) tại x=2
tìm m để
a, \(3\left|f\left(x\right)\right|+m-5=0\) có 3 nghiệm phân biệt
b,\(2f\left(\left|x\right|\right)-7+5m=0\) có 4 nghiệm pb
B1: Cho hàm số \(y=f\left(x\right)=x^2+ax-a+5\).Tìm a biết f(-2)=2004
B2: Cho hàm số \(y=f\left(x\right)=ax+b.\)Tìm và b biết f(1)=2 và f(2)=3
B3: Cho hàm số \(y=f\left(x\right)=ax^2+bx+c.\)Tìm a,b,c biết f(o)=1,f(1)=2,f(2)=3
B4:Cho hàm số y=x+1
a,tìm tọa độ điểm A, biết A là giao điểm đồ thị với trục tung
b, Tìm tọa độ điểm B biết B là giao điểm của đồ thị với trục hoành
B5: tìm tọa độ giao điểm của đồ thị hàm số y=2x và y=3x-1
B6: Cho hàm số y=ax^2+bx+c tìm a,b,c biết đồ thị hàm số đi qua điểm A(0,1), B(1,2), C(-1,0)
HELP ME!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Cho hàm số \(y = f\left( x \right) = \frac{1}{2}{x^2}\) có đồ thị \(\left( C \right)\) và điểm \(M\left( {1;\frac{1}{2}} \right)\) thuộc \(\left( C \right)\).
a) Vẽ \(\left( C \right)\) và tính \(f'\left( 1 \right)\).
b) Vẽ đường thẳng \(d\) đi qua điểm \(M\) và có hệ số góc bằng \(f'\left( 1 \right)\). Nêu nhận xét về vị trí tương đối giữa \(d\) và \(\left( C \right)\).
a)
\(\begin{array}{l}f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}{x^2} - \frac{1}{2}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {{x^2} - 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{2}\left( {x + 1} \right) = \frac{1}{2}\left( {1 + 1} \right) = 1\end{array}\)
b) Phương trình đường thẳng \(d\) đi qua điểm \(M\left( {1;\frac{1}{2}} \right)\) và có hệ số góc bằng \(k = f'\left( 1 \right) = 1\) là: \(y - \frac{1}{2} = 1\left( {x - 1} \right) \Leftrightarrow y = x - 1 + \frac{1}{2} \Leftrightarrow y = x - \frac{1}{2}\).

Đường thẳng \(d\) cắt đồ thị hàm số \(\left( C \right)\) tại duy nhất điểm \(M\left( {1;\frac{1}{2}} \right)\).
Cho hàm số \(y = f(x) = a{x^2} + bx + c\) với đồ thị là parabol (P) có đỉnh \(I\left( {\frac{5}{2}; - \frac{1}{4}} \right)\) và đi qua điểm \(A(1;2)\)
a) Biết rằng phương trình của parabol có thể viết dưới dạng \(y = a{(x - h)^2} + k\), tron đó I(h;k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.
b) Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f(x)\)
c) Giải bất phương trình \(f(x) \ge 0\)
a) Parabol: \(y = a{(x - h)^2} + k\) với \(I(h;k) = \left( {\frac{5}{2}; - \frac{1}{4}} \right)\) là tọa độ đỉnh.
\( \Rightarrow y = a{\left( {x - \frac{5}{2}} \right)^2} - \frac{1}{4}\)
(P) đi qua \(A(1;2)\) nên \(2 = a{\left( {1 - \frac{5}{2}} \right)^2} - \frac{1}{4} \Rightarrow a = 1\)
\( \Rightarrow y = {\left( {x - \frac{5}{2}} \right)^2} - \frac{1}{4} \Leftrightarrow y = {x^2} - 5x + 6\)
Vậy parabol đó là \(y = {x^2} - 5x + 6\)
b) Vẽ parabol \(y = {x^2} - 5x + 6\)
+ Đỉnh \(I\left( {\frac{5}{2}; - \frac{1}{4}} \right)\)
+ Giao với Oy tại điểm \((0;6)\)
+ Giao với Ox tại điểm \((3;0)\) và \((2;0)\)
+ Trục đối xứng \(x = \frac{5}{2}\). Điểm đối xứng với điểm \((0;6)\) qua trục đối xứng có tọa độ \((5;6)\)

b) Hàm số đồng biến trên khoảng \(\left( { - \frac{5}{2}; + \infty } \right)\)
Hàm số nghịch biến trên khoảng \(\left( { - \infty ; - \frac{5}{2}} \right)\)
c) \(f(x) \ge 0 \Leftrightarrow {x^2} - 5x + 6 \ge 0\)
Cách 1: Quan sát đồ thị, ta thấy các điểm có\(y \ge 0\) ứng với hoành độ \(x \in ( - \infty ;2] \cup [3; + \infty )\)
Do đó tập nghiệm của BPT \(f(x) \ge 0\) là \(S = ( - \infty ;2] \cup [3; + \infty )\)
Cách 2:
\(\begin{array}{l} \Leftrightarrow {x^2} - 5x + 6 \ge 0\\ \Leftrightarrow (x - 2)(x - 3) \ge 0\end{array}\)
Do đó \(x - 2\) và \(x - 3\) cùng dấu. Mà \(x - 2 > x - 3\;\forall x \in \mathbb{R}\)
\( \Leftrightarrow \left[ \begin{array}{l}x - 3 \ge 0\\x - 2 \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 3\\x \le 2\end{array} \right.\)
Tập nghiệm của BPT là \(S = ( - \infty ;2] \cup [3; + \infty )\)
Cho hàm số \(y=f\left(x\right)=ax+2\) có đồ thị đi qua điểm \(A\left(a-1;a^2+a\right)\)
a) Tìm a.
b) Vs a vừa tìm được, tìm giá trị của x thỏa mãn : \(f\left(2x-1\right)=f\left(1-2x\right)\)
Giải:
Vì đồ thị hàm số \(y=f\left(x\right)=ax+2\) đi qua điểm \(A\left(a-1;a^2+a\right)\) nên:
\(a^2+a=a\left(a-1\right)+2\)
\(\Leftrightarrow a^2+a=a^2-a+2\)
\(\Leftrightarrow2a=2\Leftrightarrow a=\dfrac{2}{2}=1\)
b) Với \(a=1\) thì \(y=f\left(x\right)=x+2\) ta có:
\(f\left(2x-1\right)=f\left(1-2x\right)\)
\(\Leftrightarrow\left(2x-1\right)+2=\left(1-2x\right)+2\)
\(\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{2}{4}=\dfrac{1}{2}\)
Cho hàm số: \(y=f\left(x\right)=ax^2+bx+c\)
a.Xác định các hệ số a,b,c biết \(f\left(0\right)=5;f\left(1\right)=0;f\left(5\right)=0\)
b.Trong hai điểm \(P\left(-1;3\right);Q\left(\dfrac{1}{2};\dfrac{9}{4}\right)\) điểm nào thuộc đồ thị hàm số
\(\left\{{}\begin{matrix}f\left(0\right)=5\Rightarrow0+0+5\Rightarrow c=5\\f\left(1\right)=0\Rightarrow a+b+5=0\\f\left(5\right)=0\Rightarrow25a+5b+5=0\end{matrix}\right.\) \(\left\{{}\begin{matrix}\left(1\right)\\\left(2\right)\\\left(3\right)\end{matrix}\right.\)
tu (3) => b =-1-5a
tu (2) => a-1-5a+5 =0 => a =1 ;b =-6
y =x^2 -6x +5
y(-1) =1 +6 +5 khac 3 => loai
y(-1/2) =1/4 -6/2 +5 =1/4 +2 = 9/4 nhan
Q(1/2;9/4) thuoc dths
83. Biết rằng hs f(x)= ax^3 + bx^2 +cx =d đạt cực đại tại điểm x =3 ,đạt cực tiểu tại điểm x =-2 . Tổng số đg tiệm cận đứng và tiệm cận ngang của đồ thị hs y = \(\dfrac{\left(x-1\right)\left(\sqrt{x+2}\right)}{\sqrt{f\left(x\right)-f\left(1\right)}}\) là?
a) Xét dấu biểu thức :
\(f\left(x\right)=2x\left(x+2\right)-\left(x+2\right)\left(x+1\right)\)
b) Lập bảng biến thiên và vẽ trong cùng một hệ tọa độ vuông góc các đồ thị của các hàm số sau :
\(y=2x\left(x+2\right)\left(C_1\right)\)
\(y=\left(x+2\right)\left(x+1\right)\left(C_2\right)\)
c) Tính các hệ số \(a,b,c\) để hàm số \(y=ax^2+bx+c\) có giá trị lớn nhất bằng 8 và đồ thị của nó đi qua A và B
a) f(x) = (x+2)(x-1)
f(x) > 0 với x < -2 hoặc x > 1
f(x) ≤ 0 với -2 ≤ x ≤ 1
b) y = 2x (x + 2) = 2(x+1)2 – 2
Bảng biến thiên:
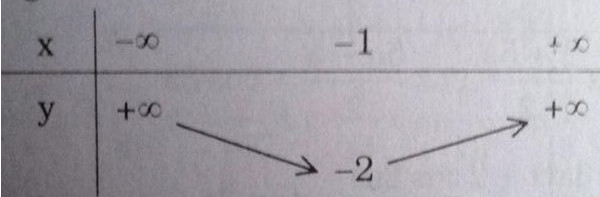
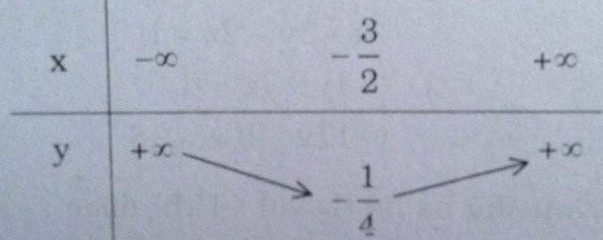
Hàm số : y = \(\left(x+2\right)\left(x+1\right)=\left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4}\)
Bảng biến thiên :
Đồ thị (C1) và (C2)
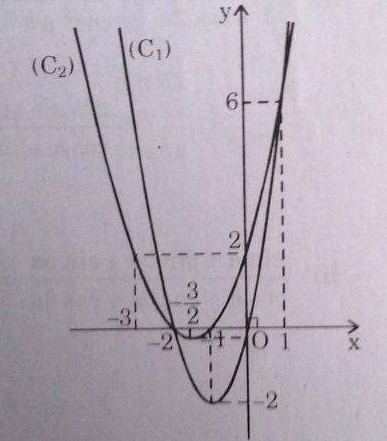
Hoành độ các giao điểm A và B của (C1) và (C2) là nghiệm của phương trình f(x) = 0 ⇔ x1 = -2, x2 = 1
⇔ A(-2, 0) , B(1, 6)
c) Giải hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{ac-b^2}{4a}\\a\left(-2\right)^2+b\left(-2\right)+c=0\\a\left(1\right)^2+b\left(1\right)+c=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2,b=0,c=8\\a=-\dfrac{2}{9},b=\dfrac{16}{9},c=\dfrac{40}{9}\end{matrix}\right.\)
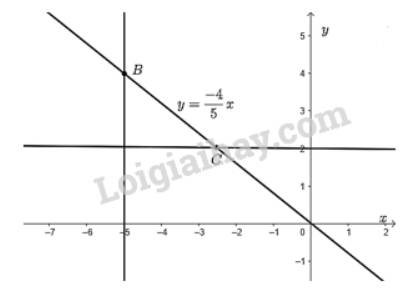
Cho biết đồ thị của hàm số \(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\).
c) Vẽ điểm trên đồ thị có tung độ bằng 2.
Từ điểm \(y = 2\) trên \(Oy\) vẽ đường thẳng vuông góc với \(Oy\) cắt đồ thị hàm số tại điểm \(C\). Khi đó, điểm \(C\) là điểm trên đồ thị hàm số có tung độ bằng 2.
Cho hàm số \(y=\frac{ax^2-bx}{x-1}\)
Tìm a và b biết rằng đồ thị (C) của hàm số đã cho đi qua điểm \(A\left(-1;\frac{5}{2}\right)\)và tiếp tuyến của (C) tại điểm O(0;0) có hệ số góc bằng -3
vì đồ thị hàm số đi qua điểm \(A\left(-1;\frac{5}{2}\right)\) nên tọa độ của A thỏa mãn phương trình sau: \(\frac{a+b}{-2}=\frac{5}{2}\Rightarrow a+b=-5\)(*)
ta tính y' có:
\(y'=\frac{\left(2ax-b\right)\left(x-1\right)-\left(ax^2-bx\right)}{\left(x-1\right)^2}=\frac{2ax^2-2ax-bx+b-ax^2+bx}{\left(x-1\right)^2}=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\)
vì hệ số góc của tiếp tuyến tại điểm O(0;0) bằng 3 nên \(y'\left(O\right)=\frac{b}{\left(0-1\right)^2}=-3\Rightarrow b=-3\)
thay b=-3 vào (*) ta tìm được a=-2
vậy a=-2;b=-3