1.

\(5=3xy+x+y\ge3xy+2\sqrt{xy}\)

\(\Leftrightarrow\left(\sqrt{xy}-1\right)\left(3\sqrt{xy}+5\right)\le0\Rightarrow xy\le1\)

\(P=\dfrac{\left(x+1\right)\left(x^2+1\right)+\left(y+1\right)\left(y^2+1\right)}{\left(x^2+1\right)\left(y^2+1\right)}-\sqrt{9-5xy}\)

\(P=\dfrac{\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^2-2xy+x+y+2}{x^2y^2+\left(x+y\right)^2-2xy+1}-\sqrt{9-5xy}\)

Đặt \(xy=a\Rightarrow0< a\le1\)

\(P=\dfrac{\left(5-3a\right)^3-3a\left(5-3a\right)+\left(5-3a\right)^2-2a+5-3a+2}{a^2+\left(5-3a\right)^2-2a+1}-\sqrt{9-5a}\)

\(P=\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{2}.2\sqrt{9-5a}\)

\(P\ge\dfrac{-27a^3+153a^2-275a+157}{10a^2-32a+26}-\dfrac{1}{4}\left(4+9-5a\right)\)

\(P\ge\dfrac{-29a^3+161a^2-277a+145}{4\left(5a^2-16a+13\right)}=\dfrac{\left(1-a\right)\left(29a^2-132a+145\right)}{4\left(5a^2-16a+13\right)}\)

\(P\ge\dfrac{\left(1-a\right)\left[29a^2+132\left(1-a\right)+13\right]}{4\left(5a^2-16a+13\right)}\ge0\)

\(P_{min}=0\) khi \(a=1\) hay \(x=y=1\)

Hai phân thức của P rất khó làm gọn bằng AM-GM hoặc Cauchy-Schwarz (nó hơi chặt)

2.

Đặt \(A=9^n+62\)

Do \(9^n⋮3\) với mọi \(n\in Z^+\) và 62 ko chia hết cho 3 nên \(A⋮̸3\)

Mặt khác tích của k số lẻ liên tiếp sẽ luôn chia hết cho 3 nếu \(k\ge3\)

\(\Rightarrow\) Bài toán thỏa mãn khi và chỉ khi \(k=2\)

Do tích của 2 số lẻ liên tiếp đều không chia hết cho 3, gọi 2 số đó lần lượt là \(6m-1\)  và \(6m+1\)

\(\Leftrightarrow\left(6m-1\right)\left(6m+1\right)=9^n+62\)

\(\Leftrightarrow36m^2=9^n+63\)

\(\Leftrightarrow4m^2=9^{n-1}+7\)

\(\Leftrightarrow\left(2m\right)^2-\left(3^{n-1}\right)^2=7\)

\(\Leftrightarrow\left(2m-3^{n-1}\right)\left(2m+3^{n-1}\right)=7\)

Pt ước số cơ bản, bạn tự giải tiếp

Theo bài ra ta có:

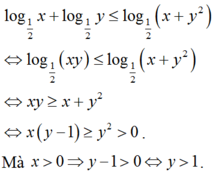
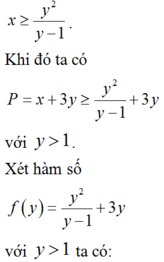
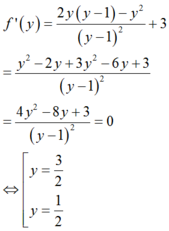
BBT:

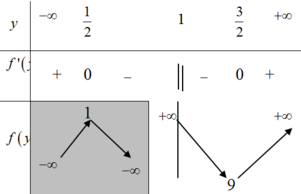
Từ BBT ta thấy

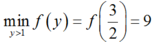
Vậy P ≥ 9  hay P m i n = 9 .     

Chọn C.

\(\Leftrightarrow\)\(4y^2+12y=4x^4+4x^2+72\)

\(\Leftrightarrow\left(2y+3\right)^2=\left(2x^2+1\right)^2+80\)

\(\Leftrightarrow\left(2y+3\right)^2-\left(2x^2+1\right)^2=80\)

\(\Leftrightarrow\left(2y+3-2x^2-1\right)\left(2y+3+2x^2+1\right)=80\)

\(\Leftrightarrow\left(y-x^2+1\right)\left(y+x^2+2\right)=20\)

Do \(x,y\in Z\) => \(y+1-x^2;y+x^2+2\in Z\)

=>\(y+1-x^2;y+x^2+2\inƯ\left(20\right)\)

Kẻ bảng làm nốt nha.

Điểm rơi: \(x=y=\frac{\sqrt{2}}{2}\)

Ta tách biểu thức được như sau: \(A=x+\frac{1}{x}+y+\frac{1}{y}=(x+\frac{1}{2x})+(y+\frac{1}{2y})+\frac{1}{2}(\frac{1}{2x}+\frac{1}{2y})\)

\(\geq 2\sqrt{x.\frac{1}{2x}}+2\sqrt{y.\frac{1}{2y}}+\frac{1}{2}.\frac{4}{x+y}=2\sqrt{2}+\frac{2}{x+y}\)

Áp dụng bất đẳng thức Bunhiacốpxki, ta lại có:

\((x+y)^2\leq 2(x^2+y^2)=2 \Rightarrow x+y\leq \sqrt{2}\)

\(\Rightarrow A\geq 3\sqrt{2}\)

Dấu bằng xảy ra khi \(x=y=\frac{\sqrt{2}}{2}\)

đây là những món quà mà bn sẽ nhận đc: 1: áo quần 2: tiền 3: đc nhiều người yêu quý 4: may mắn cả 5: luôn vui vẻ trong cuộc sống 6: đc crush thích thầm 7: học giỏi 8: trở nên xinh đẹp phật sẽ ban cho bn những điều này nếu cậu gửi tin nhắn này cho 25 người,

Bài 8:

\(F=x^2-2x+1+x^2-6x+9=2x^2-8x+10\\ F=2\left(x^2-4x+4\right)+2=2\left(x-2\right)^2+2\ge2\\ F_{min}=2\Leftrightarrow x=2\)

Bài 9:

\(A=-x^2+2x-1+5=-\left(x-1\right)^2+5\le5\\ A_{max}=5\Leftrightarrow x=1\\ B=-x^2+10x-25+2=-\left(x-5\right)^2+2\le2\\ B_{max}=2\Leftrightarrow x=5\\ C=-x^2+6x-9+9=-\left(x-3\right)^2+9\le9\\ C_{max}=9\Leftrightarrow x=3\)

a) \(6xy+4x-9y-7=0\)

  \(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)

\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)

\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)

Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)

Tự làm típ

\(A=x^3+y^3+xy\)

\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)

\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))

\(A=x^2+y^2\)

Áp dụng bất đẳng thức Bunhiakovxky ta có :

\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)

\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)

\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)

Hay \(x^3+y^3+xy\ge\frac{1}{2}\)

Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)

LOADING...

Áp dụng bất đẳng thức Svacxo và bất đẳng thức \(\frac{1}{4ab}\ge\frac{1}{\left(a+b\right)^2}\)ta có :

\(Q=\frac{2}{x^2+y^2}+\frac{2}{2xy}+\frac{4}{2xy}=2\left(\frac{1}{x^2+y^2}+\frac{1}{2xy}\right)+\frac{8}{4xy}\)

\(\ge2\frac{\left(1+1\right)^2}{\left(x+y\right)^2}+\frac{8}{\left(x+y\right)^2}=\frac{2.4}{2^2}+\frac{8}{2^2}=\frac{16}{4}=4\)

Dấu "=" xảy ra khi và chỉ khi \(x=y=1\)

Vậy min Q = 4 khi x = y = 1