\(a,5x\left(x^2-9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=9\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ b,3\left(x+3\right)-x^2-3x=0\\ \Leftrightarrow3\left(x+3\right)-x\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(3-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\\ c,x^2-9x-10=0\\ \Leftrightarrow x^2+x-10x-10=0\\ \Leftrightarrow x\left(x+1\right)-10\left(x+1\right)=0\\ \Leftrightarrow\left(x-10\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)

a, 5\(x\)(\(x^2\) - 9) = 0

    \(\left[{}\begin{matrix}x=0\\x^2-9=0\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\) 

Vậy \(x\) \(\in\) { -3; 0; 3}

b, 3.(\(x+3\)) - \(x^2\) - 3\(x\) = 0

    3.(\(x+3\)) - \(x\).( \(x\) + 3) = 0

    (\(x+3\))( 3 - \(x\)) = 0

     \(\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)

Vậy \(x\) \(\in\){ -3; 3}

c, \(x^2\) - 9\(x\) - 10 = 0

   \(x^2\) + \(x\) - 10\(x\)  - 10 = 0

   \(x.\left(x+1\right)\) - 10.( \(x-1\)) = 0

        (\(x+1\))(\(x-10\)) = 0

         \(\left[{}\begin{matrix}x+1=0\\x-10=0\end{matrix}\right.\)

           \(\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)

Vậy \(x\) \(\in\){ -1; 10}

a) 5x(x2-9)=0

=> TH1 5x=0

      <=> x= 0

     TH2: 2x-9=0

       <=> 2x=9

       <=> x = \(\dfrac{9}{2}\)

b, 3(x+3) - x²- 3x = 0   

<=> 3x + 9 - x² -3x = 0

<=> - x² +9 = 0

<=> - x² = -9

 <=> x = 3

c, x² -9x -10 = 0

<=> x² -x + 10x -10 = 0

<=> x(x-1)+10(x-1)=0     

 <=> (x-1)(x+10)=0

=> TH1: x-1=0

       <=> x=1

      TH2: x +10=0

      <=>  x=-10

\(a,\Leftrightarrow x\left(x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\\ b,\Leftrightarrow\left(x+4-4\right)\left(x+4+4\right)=0\\ \Leftrightarrow x\left(x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\\ c,\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\\ d,\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x=5\)

a) \(\Leftrightarrow x\left(x+9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\)

b) \(\Leftrightarrow x\left(x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)

c) \(\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)

d) \(\Leftrightarrow\left(x-5\right)^2=0\\ \Leftrightarrow x=5\)

\(1,\Leftrightarrow x\left(x-9\right)=0\Leftrightarrow\left[{}\begin{matrix}x=9\\x=0\end{matrix}\right.\\ 2,\Leftrightarrow x^2-4x-x^2=7\Leftrightarrow-4x=7\Leftrightarrow x=-\dfrac{7}{4}\\ 3,\Leftrightarrow3x+2x-10=5\Leftrightarrow5x=15\Leftrightarrow x=3\\ 4,\Leftrightarrow\left(5x-1\right)\left(5x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=-\dfrac{1}{5}\end{matrix}\right.\\ 5,\Leftrightarrow\left(x-2\right)\left(3x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{5}{3}\end{matrix}\right.\\ 6,\Leftrightarrow\left(x-7\right)\left(3x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-\dfrac{4}{3}\end{matrix}\right.\)

\(7,\Leftrightarrow\left(2x-3\right)\left(2x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\\ 8,\Leftrightarrow\left(x-4\right)\left(10x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{5}\\x=4\end{matrix}\right.\\ 9,\Leftrightarrow2x^2-5x-2x^2=0\Leftrightarrow x=0\\ 10,\Leftrightarrow2x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\\ 11,\Leftrightarrow\left(4x-3\right)\left(3-2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=\dfrac{3}{2}\end{matrix}\right.\\ 12,\Leftrightarrow2x^2-10x-2x^2=3\Leftrightarrow-10x=3\Leftrightarrow x=-\dfrac{3}{10}\)

\(1,\Leftrightarrow x\left(x-9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\\ 2,\Leftrightarrow x^2-4x-x^2=7\\ \Leftrightarrow-4x=7\\ \Leftrightarrow x=\dfrac{-7}{4}\\ 3,\Leftrightarrow3x+2x-10=5\\ \Leftrightarrow5x=15\\ \Leftrightarrow x=3\\ 4,\Leftrightarrow\left(5x-1\right)\left(5x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=-\dfrac{1}{5}\end{matrix}\right.\)

\(5,\Leftrightarrow\left(x-2\right)\left(3x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{5}{3}\end{matrix}\right.\\ 6,\Leftrightarrow\left(3x+4\right)\left(x-7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=7\end{matrix}\right.\\ 7,\Leftrightarrow\left(2x-3\right)\left(2x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

\(8,\Leftrightarrow10x\left(x-4\right)+2\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(10x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{1}{5}\end{matrix}\right.\\ 9,\Leftrightarrow2x^2-5x-2x^2=0\\ \Leftrightarrow-5x=0\\ \Leftrightarrow x=0\\ 10,\Leftrightarrow2x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

\(11,\Leftrightarrow\left(2x-3\right)\left(4x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{3}{4}\end{matrix}\right.\\ 12,\Leftrightarrow2x^2-10x-2x^2=3\\ \Leftrightarrow-10x=3\\ \Leftrightarrow x=-\dfrac{3}{10}\)

1) \(x^2-9x=0\Rightarrow x\left(x-9\right)=0\Rightarrow x=0;9\)

2) \(x\left(x-4\right)-x^2=7\Rightarrow-4x=7\Rightarrow x=-\dfrac{7}{4}\)

3) \(3x+2\left(x-5\right)=5\Rightarrow5x-10=5\Rightarrow5x=15\Rightarrow x=3\)

4) \(25x^2-1=0\Rightarrow x^2=\dfrac{1}{25}\Rightarrow x=\pm\dfrac{1}{5}\)

5) \(3x\left(x-2\right)-5\left(x-2\right)=0\Rightarrow\left(x-2\right)\left(3x-5\right)=0\Rightarrow x=2;\dfrac{5}{3}\)

6) \(3x\left(x-7\right)+4\left(x-7\right)\Rightarrow\left(3x+4\right)\left(x-7\right)=0\Rightarrow x=-\dfrac{4}{3};7\)

7) \(4x^2-9=0\Rightarrow x^2=\dfrac{9}{4}\Rightarrow x=\pm\dfrac{3}{2}\)

8) \(10x\left(x-4\right)+2x-8=0\Rightarrow2\left(x-4\right)\left(5x+1\right)=0\Rightarrow x=4;-\dfrac{1}{5}\)

9) \(x\left(2x-5\right)-2x^2=0\Rightarrow x\left(2x-5-2x=0\right)\Rightarrow x=0\)

10) \(2x^2-4x=0\Rightarrow2x\left(x-2\right)=0\Rightarrow x=0;2\)

11) \(2x\left(3-4x\right)+3\left(4x-3\right)=0\Rightarrow2x\left(4x-3\right)-3\left(4x-3\right)=0\Rightarrow\left(4x-3\right)\left(2x-3\right)=0\Rightarrow x=\dfrac{3}{4};\dfrac{3}{2}\)

12) \(2x\left(x-5\right)-2x^2=3\Rightarrow-10x=3\Rightarrow x=-\dfrac{3}{10}\)

\(a,\Leftrightarrow x^3-8-x^3-2x=12\Leftrightarrow-2x=20\Leftrightarrow x=-10\\ b,\Leftrightarrow x^2-6x+9-x^2+4=16\Leftrightarrow=-6x=3\Leftrightarrow x=-\dfrac{1}{2}\\ c,\Leftrightarrow x\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ d,\Leftrightarrow x^2\left(x-6\right)+9\left(x-6\right)=0\\ \Leftrightarrow\left(x^2+9\right)\left(x-6\right)=0\\ \Leftrightarrow x=6\left(x^2+9>0\right)\)

a)\(\left(x-2\right)^2-\left(2x+3\right)^2=0\Rightarrow\left(x-2+2x+3\right)\left(x-2-2x-3\right)=0\)

\(\Rightarrow\left(3x+1\right)\left(-x-5\right)=0\Rightarrow\left[{}\begin{matrix}3x+1=0\\-x-5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-5\end{matrix}\right.\)

b)\(9\left(2x+1\right)^2-4\left(x+1\right)^2=0\Rightarrow\left[3\left(2x+1\right)+2\left(x+1\right)\right]\left[3\left(2x+1\right)-2\left(x+1\right)\right]=0\)

\(\Rightarrow\left[8x+5\right]\left[4x+1\right]=0\Rightarrow\left[{}\begin{matrix}8x+5=0\\4x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{8}\\x=\dfrac{1}{4}\end{matrix}\right.\)

c)\(x^3-6x^2+9x=0\Rightarrow x\left(x^2-6x+9\right)=0\Rightarrow x\left(x-3\right)^2=0\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)

d) \(x^2\left(x+1\right)-x\left(x+1\right)+x\left(x-1\right)=0\)

\(\Rightarrow x\left(x+1\right)\left(x^2-1\right)+x\left(x-1\right)=0\)

\(\Rightarrow x\left(x+1\right)\left(x-1\right)\left(x+1\right)+x\left(x-1\right)=0\)

\(\Rightarrow x\left(x-1\right)\left[\left(x+1\right)\left(x+1\right)+1\right]=0\)

\(\Rightarrow x\left(x-1\right)\left[\left(x+1\right)^2+1\right]=0\)

Do \(\left(x+1\right)^2+1>0\)

\(\Rightarrow x\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x-1=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

a) \(\left(x+2\right)^3-x^2\left(x+6\right)=0\)

\(\Leftrightarrow x^3+6x^2+12x+8-x^3-6x^2=0\)

\(\Leftrightarrow12x+8=0\)

\(\Leftrightarrow12x=-8\)

\(\Leftrightarrow x=-\dfrac{8}{12}\)

\(\Leftrightarrow x=-\dfrac{2}{3}\)

b) \(\left(2x+3\right)^3-8x\left(x+1\right)\left(x-1\right)=9x\left(4x-3\right)\)

\(\Leftrightarrow8x^3+36x^2+54x+27-8x\left(x^2-1\right)=36x^2-27x\)

\(\Leftrightarrow8x^3+36x^2+54x+27-8x^3+8x=36x^2-27x\)

\(\Leftrightarrow8x^3-8x^3+36x^2-36x^2+54x+27x+8x+27=0\)

\(\Leftrightarrow89x+27=0\)

\(\Leftrightarrow x=-\dfrac{27}{89}\)

c) \(\left(2-x\right)^3+\left(2+x\right)^3-12x\left(x+1\right)=0\)

\(\Leftrightarrow8-12x+6x^2-x^3+8+12x+6x^2+x^3-12x^2-12x=0\)

\(\Leftrightarrow\left(x^3-x^3\right)+\left(6x^2+6x^2-12x^2\right)-\left(12x-12x\right)+12x+\left(8+8\right)=0\)

\(\Leftrightarrow12x+16=0\)

\(\Leftrightarrow x=-\dfrac{16}{12}\)

\(\Leftrightarrow x=-\dfrac{4}{3}\)

`#040911`

`a)`

`(x + 2)^3 - x^2(x + 6) = 0`

`<=> x^3 + 6x^2 + 12x + 8 - x^3 - 6x^2 = 0`

`<=> (x^3 - x^3) + (6x^2 - 6x^2) + 12x = 0`

`<=> 12x = 0`

`<=> x = 0`

Vậy, `x = 0.`

`b)`

`(2x + 3)^3 - 8x(x - 1)(x + 1) = 9x(4x - 3)`

`<=> 8x^3 + 36x^2 + 54x + 27 - 8x(x^2 - 1) = 36x^2 - 27x`

`<=> 8x^3 + 36x^2 + 54x + 27 - 8x^3 + 8x - 36x^2 + 27x = 0`

`<=> (8x^3 - 8x^3) + (36x^2 - 36x^2) + (54x + 8x + 27x) + 27 = 0`

`<=> 89x + 27 = 0`

`<=> 89x = -27`

`<=> x = -27/89`

Vậy, `x = -27/89`

`c)`

`(2 - x)^3 + (2 + x)^3 - 12x(x + 1) = 0`

`<=> 8 - 12x + 6x^2 - x^3 + 8 + 12x + 6x^2 + x^3 - 12x^2 - 12x = 0`

`<=> (-x^3 + x^3) + (12x - 12x - 12x) + (6x^2 + 6x^2 - 12x^2) + (8 + 8)=0`

`<=> -12x + 16 = 0`

`<=> -12x = -16`

`<=> 12x = 16`

`<=> x=4/3`

Vậy, `x = 4/3.`

\(a,\Leftrightarrow x\left(2x-7\right)+2\left(2x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(2x-7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{7}{2}\end{matrix}\right.\\ b,\Leftrightarrow x\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ c,\Leftrightarrow\left(2x-1\right)\left(2x+1\right)-2\left(2x-1\right)^2=0\\ \Leftrightarrow\left(2x-1\right)\left(2x+1-4x+2\right)=0\\ \Leftrightarrow\left(2x-1\right)\left(-2x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\\ d,\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

a) √16x = 8 (điều kiện: x ≥ 0)

⇔ 16x = 82 ⇔ 16x = 64 ⇔ x = 4

(Hoặc: √16x = 8 ⇔ √16.√x = 8

⇔ 4√x = 8 ⇔ √x = 2 ⇔ x = 4)

b) điều kiện: x ≥ 0

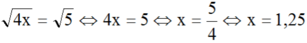
c) điều kiện: x - 1 ≥ 0 ⇔ x ≥ 1 (*)

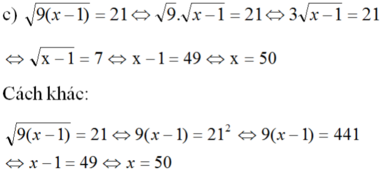
x = 50 thỏa mãn điều kiện (*) nên x = 50 là nghiệm của phương trình.

d) Vì (1 - x)2 ≥ 0 ∀x nên phương trình xác định với mọi giá trị của x.

- Khi 1 – x ≥ 0 ⇔ x ≤ 1

Ta có: 2|1 – x| = 6 ⇔ 2(1 – x) = 6 ⇔ 2(1 – x) = 6

⇔ –2x = 4 ⇔ x = –2 (nhận)

- Khi 1 – x < 0 ⇔ x > 1

Ta có: 2|1 – x| = 6 ⇔ 2[– (1 – x)] = 6

⇔ x – 1 = 3 ⇔ x = 4 (nhận)

Vậy phương trình có hai nghiệm: x = - 2; x = 4