Chứng minh rằng: x2 - x + 1 > 0 với mọi số thực x?

Những câu hỏi liên quan
Chứng minh rằng x2 – x + 1 > 0 với mọi số thực x
Ta có:
\(x^2-x+1\)
\(=x^2-2\cdot\dfrac{1}{2}\cdot x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(x-\dfrac{1}{2}\right)^2\ge0\forall x\) và \(\dfrac{3}{4}>0\)
Nên: \(x^2-x+1>0\)
Đúng 2
Bình luận (0)
\(x^2-x+1\)
\(=x^2-\dfrac{1}{2}.x-\dfrac{1}{2}.x+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=x\left(x-\dfrac{1}{2}\right)-\dfrac{1}{2}\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)\left(x-\dfrac{1}{2}\right)+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) với mọi x ( đpcm )
Đúng 1
Bình luận (0)
\(x^2-x+1=x^2-2.x.\dfrac{1}{2}+\left(\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\\ Mà:\left(x-\dfrac{1}{2}\right)^2>0\forall x\in R\\ Vậy:\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\in R\\ Vậy:x^2-x+1>0\forall x\in R\)
Đúng 2
Bình luận (0)
chứng minh rằng x2>2(x-1) với mọi số thực x
x2 > 2( x - 1 )
<=> x2 - 2x + 2 > 0
<=> ( x2 - 2x + 1 ) + 1 > 0
<=> ( x - 1 )2 + 1 > 0 ( luôn đúng ∀ x ∈ R )
Vậy bđt ban đầu được chứng minh
Đúng 1
Bình luận (0)
Chứng minh: x – x2 – 1 < 0 với mọi số thực x.
Ta có:
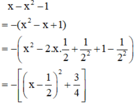
Ta có: 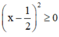 với mọi số thực x
với mọi số thực x
⇒ 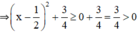 với mọi số thực x
với mọi số thực x
⇒ 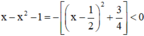 với mọi số thực (ĐPCM)
với mọi số thực (ĐPCM)
Đúng 0
Bình luận (0)
Bài 6: Chứng minh rằng:a) x2 – x + 1 0 với mọi số thực x b) -x2+2x -4 0 với mọi số thực xBài 7: Tính nhanh giá trị biểu thức: tại x 18; y 4 b) (2x + 1)2 + (2x - 1)2 - 2(1 + 2x)(1 - 2x) tại x 100
Đọc tiếp
Bài 6: Chứng minh rằng:
a) x2 – x + 1 > 0 với mọi số thực x
b) -x2+2x -4 < 0 với mọi số thực x![]()
Bài 7: Tính nhanh giá trị biểu thức:
![]() tại x = 18; y = 4
tại x = 18; y = 4
b) (2x + 1)2 + (2x - 1)2 - 2(1 + 2x)(1 - 2x) tại x = 100
a) x2 – x + 1
=(x2 – x + 1/4 )+3/4
=(x-1/2)2+3/4
ta có (x-1/2)2>=0
(x-1/2)2+3/4>=+3/4>0
vậy (x-1/2)2+3/4>0 với mọi số thực x
b) -x2+2x -4
= -x2+2x -1-3
=-(x2-2x +1)-3
=-(x-2)2-3
ta có (x-2)2>=0
=>-(x-2)2=<0
=>-(x-2)2-3=<-3<0
vậy -(x-2)2-3<0 với mọi số thực x
Đúng 0
Bình luận (0)
Chứng minh: x2 – 2xy + y2 + 1 > 0 với mọi số thực x và y.
Ta có:
x2 – 2xy + y2 + 1
= (x2 – 2xy + y2) + 1
= (x – y)2 + 1.
(x – y)2 ≥ 0 với mọi x, y ∈ R
⇒ x2 – 2xy + y2 + 1 = (x – y)2 + 1 ≥ 0 + 1 = 1 > 0 với mọi x, y ∈ R (ĐPCM).
Đúng 0
Bình luận (0)
Chứng minh rằng: x2 - 2x +3 ≥ 2 với mọi số thực x
Chứng minh -x2 + 3x - 4 < 0 với mọi số thực x
Ta có: \(-x^2+3x-4\)
\(=-\left(x^2-3x+4\right)\)
\(=-\left(x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{7}{4}\right)\)
\(=-\left(x-\dfrac{3}{2}\right)^2-\dfrac{7}{4}< 0\forall x\)
Đúng 2
Bình luận (0)
$-x^2+3x-4\\=-x^2+2.x.\dfrac{3}{2}-\dfrac{9}{4}-\dfrac{7}{4}\\=-(x-\dfrac{3}{2})^2-\dfrac{7}{4}<0$
=> ĐPCM
Đúng 1
Bình luận (0)
Chứng minh rằng
x^2-2xy+y^2+1>0 với mọi số thực x và y
x-x^2-1<0 với mọi số thực x
Ta có : x2 - 2xy + y2 + 1 = (x - y)2 + 1
Vì : \(\left(x-y\right)^2\ge0\forall x\in R\)
Nên : \(\left(x-y\right)^2+1\ge1\forall x\in R\)
Suy ra : \(\left(x-y\right)^2+1>0\forall x\in R\)
Vậy x2 - 2xy + y2 + 1 \(>0\forall x\in R\)
Ta có : x - x2 - 1
= -(x2 - x + 1)
\(=-\left(x^2-x+\frac{1}{4}+\frac{3}{4}\right)\)
\(=-\left(x^2-x+\frac{1}{4}\right)-\frac{3}{4}\)
\(=-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}\)
Vì : \(-\left(x-\frac{1}{2}\right)^2\le0\forall x\in R\)
Nên : \(-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}\le-\frac{3}{4}< 0\)
Vậy x - x2 - 1 \(< 0\forall x\in R\)
Đúng 0
Bình luận (0)
hỏi tí cái chữ A ngược đó là gì vậy bạn
Đúng 0
Bình luận (0)
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 =0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| < |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)
2 = 0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2























