Bài 3:

Ta có: \(2n^2+n-7⋮n-2\)

\(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)

\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)

hay \(n\in\left\{3;1;5;-1\right\}\)

\(a,A=\left(x^2-4xy+4y^2\right)+10\left(x-2y\right)+25+\left(y^2-2y+1\right)+2\\ A=\left(x-2y\right)^2+10\left(x-2y\right)+5+\left(y-1\right)^2+2\\ A=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\)

Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=2y-5\\y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)

\(b,\Leftrightarrow3x^3+10x^2-5+n=\left(3x+1\right)\cdot a\left(x\right)\)

Thay \(x=-\dfrac{1}{3}\Leftrightarrow3\left(-\dfrac{1}{27}\right)+10\cdot\dfrac{1}{9}-5+n=0\)

\(\Leftrightarrow-\dfrac{1}{9}+\dfrac{10}{9}-5+n=0\\ \Leftrightarrow-4+n=0\Leftrightarrow n=4\)

\(c,\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\\ \Leftrightarrow2n\left(n-2\right)+5\left(n-2\right)+3⋮n-2\\ \Leftrightarrow n-2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow n\in\left\{-1;1;3;5\right\}\)

Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:

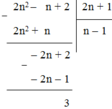
2n2 – n + 2 chia hết cho 2n + 1

⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3)

⇔ 2n + 1 ∈ {±1; ±3}

   + 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0

   + 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1

   + 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1

   + 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.

Vậy n ∈ {-2; -1; 0; 1.}

Cách 2:

Ta có:

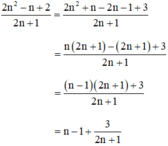
2n2 – n + 2 chia hết cho 2n + 1

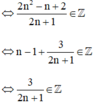
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.

   + 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0

   + 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1

   + 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1

   + 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.

Vậy n ∈ {-2; -1; 0; 1.}

Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.

Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:

2n² – n + 2 chia hết cho 2n + 1

<=> 3 \(⋮\)( 2n + 1 ) hay ( 2n + 1 ) \(\in\) Ư(3)

<=> 2n + 1 \(\in\) {\(\pm\)1; \(\pm\)3 }

   + 2n + 1 = 1 <=> 2n = 0 <=> n = 0

   + 2n + 1 = -1 <=> 2n = -2 <=> n = -1

   + 2n + 1 = 3 <=> 2n = 2 <=> n = 1

   + 2n + 1 = -3 <=> 2n = -4 <=> n = -2.

Vậy n \(\in\) { -2 ; -1 ; 0 ; 1 }

Bài 1:

\(=-5^{22}+222+[-122-(100-5^{22})+2022]\)

\(=-5^{22}+222-122-100+5^{22}+2022\\ =(-5^{22}+5^{22})+(222-122-100)+2022\\ =0+0+2022=2022\)

Bài 2:

$2n^2+n-6\vdots 2n+1$

$\Rightarrow n(2n+1)-6\vdots 2n+1$

$\Rightarrow 6\vdots 2n+1$

$\Rightarrow 2n+1\in Ư(6)$

Mà $2n+1$ lẻ nên $2n+1\in \left\{\pm 1; \pm 3\right\}$

$\Rightarrow n\in \left\{0; -1; 1; -2\right\}$

\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)

hay \(n\in\left\{3;1;5;-1\right\}\)

Câu 2: 

\(=\dfrac{x^2\left(2x-5\right)+3\left(2x-5\right)}{2x-5}=x^2+3\)

Câu 3: 

\(\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\)

\(\Leftrightarrow n-2\in\left\{1;-1;3;-3\right\}\)

hay \(n\in\left\{3;1;5;-1\right\}\)

Câu b : Bạn có nhầm đề không vậy ?

\(a,n^3-2n^2+3n+3=n^3-n^2-n^2+n+2n-2+5\\ =\left(n-1\right)\left(n^2-n+2\right)+5\\ \Leftrightarrow n^3-2n^2+3n+3⋮\left(n-1\right)\\ \Leftrightarrow5⋮n-1\\ \Leftrightarrow n-1\in\left\{-5;-1;1;5\right\}\\ \Leftrightarrow n\in\left\{-4;0;2;6\right\}\)

\(b,\Leftrightarrow x^4+6x^3+7x^2-6x+a\\ =x^4+3x^3-x^2+3x^3+9x^2-3x-x^2-3x+1-1+a\\ =\left(x^2+3x-1\right)\left(x^2+3x-1\right)-1+a\\ =\left(x^2+3x-1\right)^2+a-1\)

Để \(x^4+6x^3+7x^2-6x+a⋮x^2+3x-1\)

\(\Leftrightarrow a-1=0\Leftrightarrow a=1\)

\(A:B=\left(2n^2-4n+3n-6+3\right):\left(n-2\right)\\ =\left[2n\left(n-2\right)+3\left(n-2\right)+3\right]:\left(n-2\right)=2n+3\left(\text{dư }3\right)\)

Để phép chia hết \(\Rightarrow n-2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\)

\(\Rightarrow n\in\left\{-1;1;3;5\right\}\)

theo đề ta có:

\(\dfrac{A}{B}=\dfrac{2n^2-n-3}{n-2}=\dfrac{2n^2-4n+3n-6+3}{n-2}\)

=\(\dfrac{2n\left(n-2\right)+3\left(n-2\right)+3}{n-2}\)

=\(\dfrac{\left(n-2\right)\left(2n+6\right)}{n-2}=\dfrac{2n+6}{1}=2n+6\)

Vậy đa thức A chia hết cho đa thức B