Cho đường tròn (O) đường kính BC; MA,MC là hai tiếp tuyến của đường tròn (O); \(\widehat{ABC}\)= 70 độ. Tính số đo góc AMC

Những câu hỏi liên quan
cho nửa đường tròn tâm O đường kính BC.Điểm A thuộc nửa đường tròn tâm O khác B và C.Kẻ AH vuông góc BC (H inBC). Trên nửa mặt phẳng bờ BC chứa A vẽ nửa đường tròn tâm I đường kính BH và nửa đường tròn tâm K đường kính CH , chúng lần lượt cắt AB , AC ở D và E. a,Chứng minh: tứ giác BCED nội tiếpb,Gọi M,N lần lượt là các điểm đối xứng H qua AB và AC.Chứng minh MN là tiếp tuyến của nửa đường tròn tâm Oc,Biết BC50 cm , DE20 cm .Tính diện tích hình được giới hạn bởi 3 nửa đường tròn tâm O,I,K
Đọc tiếp
cho nửa đường tròn tâm O đường kính BC.Điểm A thuộc nửa đường tròn tâm O khác B và C.Kẻ AH vuông góc BC (H \(\in\)BC). Trên nửa mặt phẳng bờ BC chứa A vẽ nửa đường tròn tâm I đường kính BH và nửa đường tròn tâm K đường kính CH , chúng lần lượt cắt AB , AC ở D và E.
a,Chứng minh: tứ giác BCED nội tiếp
b,Gọi M,N lần lượt là các điểm đối xứng H qua AB và AC.Chứng minh MN là tiếp tuyến của nửa đường tròn tâm O
c,Biết BC=50 cm , DE=20 cm .Tính diện tích hình được giới hạn bởi 3 nửa đường tròn tâm O,I,K
Cho 2 đường tròn (O) và (O') tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O'). Đường tròn đường kính OC cắt (O) tại M và N
a) đường thẳng CM cắt (O') tại P. CM OM // BP
b) Từ C kẻ đường thẳng vuông góc với CM cắt tia ON tại D. CM tam giác OCD là tam giác cân
a: Xét (OC/2) có
góc OMC là góc nội tiếp chắn nửa đường tròn
=>góc OMC=90 độ
=>CM vuông góc MO
Xét (O') có
góc BPC nội tiếp
BC là đường kính
=>góc BPC=90 độ
=>BP vuông góc CM
=>BP//OM
Đúng 0
Bình luận (0)
Cho đường trong (O) bán kính OA. Từ trung điểm M của OA vẽ dây BC ^ OA. Biết độ dài đường tròn (O) 4π cm. Tính:
a, Bán kính đường tròn (O)
b, Độ dài hai cung BC của đường tròn

a, 2πR = 4π => R = 2cm
b, A O B ^ = 60 0 (DOAB đều)
=> B O C ^ = 120 0
l B C ⏜ n h ỏ = π . R . 120 180 = 4 π 3 cm
và l B C ⏜ l ớ n = 8 3 π cm
Đúng 1
Bình luận (0)
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại B. Vẽ đường kính AB của đường tròn (O) và đường kính BC của đường tròn (O’). Đường tròn đường kính OC cắt (O) tại M và N. a/ Đường thẳng CM cắt (O’) tại P. Chứng minh: OM//BP. b/ Từ C kẻ đường thẳng vuông góc với CM cắt tia ON tại D. Chứng minh: Tam giác OCD là tam giác cân.
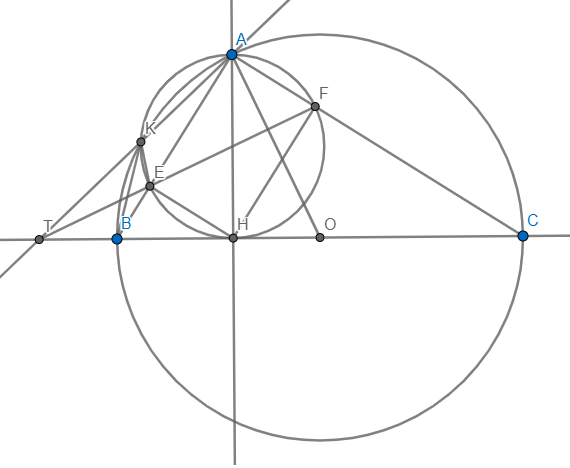
Cho đường tròn tâm O, đường kính BC. A thuộc đường tròn tâm O. AH vuông góc BC. Đường tròn đường kính AH cắt AB, AC và cắt đường tròn tâm O tại E, F, K.
a) Chứng minh: AO vuông góc EF.
b) AK cắt BC tại T. Chứng minh: T, E, F thẳng hàng.
Mọi người giúp em với ạ em cần gấp
a) Vì AH là đường kính \(\Rightarrow\angle AEH=\angle AFH=90\)
Vì BC là đường kính \(\Rightarrow\angle BAC=90\Rightarrow\angle AEH=\angle AFH=\angle EAF=90\)
\(\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow\angle AEF=\angle AHF=\angle ACH\left(=90-\angle HAC\right)\)
\(\Rightarrow\angle AEF+\angle ABC=\angle ACH+\angle ABC=90\)
mà \(\angle ABC=\angle BAO\) (\(\Delta ABO\) cân tại O)
\(\Rightarrow\angle AEF+\angle BAO=90\Rightarrow EF\bot AO\)
c) EF cắt BC tại T'.T'A cắt (O) tại K'
Vì \(\angle AEF=\angle ACH\Rightarrow EFCB\) nội tiếp
Xét \(\Delta T'EB\) và \(\Delta T'CF:\) Ta có: \(\left\{{}\begin{matrix}\angle T'EB=\angle T'CF\\\angle FT'Cchung\end{matrix}\right.\)
\(\Rightarrow\Delta T'EB\sim\Delta T'CF\left(g-g\right)\Rightarrow\dfrac{T'E}{T'C}=\dfrac{T'B}{T'F}\Rightarrow T'E.T'F=T'B.T'C\)
Vì AK'BC nội tiếp \(\Rightarrow\angle T'K'B=\angle T'CA\)
Xét \(\Delta T'K'B\) và \(\Delta T'CA:\) Ta có: \(\left\{{}\begin{matrix}\angle T'K'B=\angle T'CA\\\angle AT'Cchung\end{matrix}\right.\)
\(\Rightarrow\Delta T'K'B\sim\Delta T'CA\left(g-g\right)\Rightarrow\dfrac{T'K'}{T'C}=\dfrac{T'B}{T'A}\Rightarrow T'K'.T'A=T'B.T'C\)
\(\Rightarrow T'K'.T'A=T'E.T'F\Rightarrow\dfrac{T'K'}{T'F}=\dfrac{T'E}{T'A}\)
Xét \(\Delta T'EK'\) và \(\Delta T'AF:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{T'K'}{T'F}=\dfrac{T'E}{T'A}\\\angle FT'Achung\end{matrix}\right.\)
\(\Rightarrow\Delta T'EK'\sim\Delta T'AF\left(c-g-c\right)\Rightarrow\angle T'K'E=\angle T'FA\)
\(\Rightarrow AK'EF\) nội tiếp \(\Rightarrow K'\in\) đường tròn đường kính AH
\(\Rightarrow K'\equiv K\Rightarrow T'\equiv T\Rightarrow T,E,F\) thẳng hàng
Đúng 1
Bình luận (1)
Cho đường tròn (O;R) có đường kính BC. Trên tia đối của tia BC lấy cung DE của đường tròn (O) vuông góc với BCa) AE là tiếp tuyến của đường tròn (O)b) Vẽ đường kính DF của đường tròn (O). Gọi P là giao điểm của EC và DF, G là giao điểm của 2 đường thẳng BD và AE. Chứng minh BC//EF và PO.GEPC.GBc) Vẽ cát tuyến AMN của đường tròn (O) ( cát tuyến không đi qua O ), các tuyến tại M và N của đường tròn (O) cắt nhau tại K. Chứng minh ba điểm K,D,E thẳng hàng.
Đọc tiếp
Cho đường tròn (O;R) có đường kính BC. Trên tia đối của tia BC lấy cung DE của đường tròn (O) vuông góc với BC
a) AE là tiếp tuyến của đường tròn (O)
b) Vẽ đường kính DF của đường tròn (O). Gọi P là giao điểm của EC và DF, G là giao điểm của 2 đường thẳng BD và AE. Chứng minh BC//EF và PO.GE=PC.GB
c) Vẽ cát tuyến AMN của đường tròn (O) ( cát tuyến không đi qua O ), các tuyến tại M và N của đường tròn (O) cắt nhau tại K. Chứng minh ba điểm K,D,E thẳng hàng.
Cho đường tròn O. Bán kính R. Đường kính AB dây AC. Biết cách từ O đến AC và BC lần lượt là 6 và 8. Tính AC, BC và bán kính của đường tròn .
Cho \(\Delta ABC\) cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường tròn ở D.
1) Vì sao AD là đường kính của đường tròn (O)
2) Tính \(\widehat{ACD}\)
3) Cho BC = 24cm; AC = 20cm. Tính đường cao AH và bán kính đường tròn (O)
1: ΔABC cân tại A
=>AB=AC
mà OB=OC
nên AO là trung trực của BC
=>AD là đường kính của (O)
2: Xét (O) có
góc ACD là góc nội tiếp chắn nửa đường tròn
=>góc ACD=90 độ
3: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=BC/2=12cm
AH=căn AB^2-AH^2=16cm
ΔACD vuông tại C có CH là đường cao
nên AC^2=AH*AD
=>AD=20^2/16=25cm
=>R=12,5cm
Đúng 1
Bình luận (0)
Cho đường tròn O bán kính R, dây BC khác đường kính, qua O kẻ đường vuông góc với BC tại I cắt tiếp tuyến tại B của đường tròn, tại điểm A ve đường kính BD
a, CM: CD song song với OA
b, CM: AC là tiếp tuyến của đường tròn O
c, Đường thẳng vuông góc với BD tại O cắt BC tại K. CM: IK.IC + OI.IA = R2
a: Xét (O) có
ΔBCD nội tiếp
BD là đường kính
=>ΔBCD vuông tại C
=>CD//OA
b: ΔOBC cân tại O
mà OA là đường cao
nên OA là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
góc BOA=góc COA
OA chung
=>ΔOBA=ΔOCA
=>góc OCA=90 độ
=>AC là tiêp tuyến của (O)
Đúng 1
Bình luận (0)
cho đường tròn (O;R) , dây BCneđường kính . 2 tiếp tuyến của đg tròn tại B và C cắt nhau tại A. Kẻ đường kính CD . Kẻ BH vuông góc CD tại Ha, CM: A,B,O,C cùng thuộc 1 đường tròn . Xác định tâm,bán kính đường tròn đób, CM : AO vuông góc BC . Tính AB,OA biết R1,5 và BC24 c, CM: BC là phân giác góc ABHd, I là giao điểm AD và BH , BD giao AC tại E . CM : IHIB
Đọc tiếp
cho đường tròn (O;R) , dây BC\(\ne\)đường kính . 2 tiếp tuyến của đg tròn tại B và C cắt nhau tại A. Kẻ đường kính CD . Kẻ BH vuông góc CD tại H
a, CM: A,B,O,C cùng thuộc 1 đường tròn . Xác định tâm,bán kính đường tròn đó
b, CM : AO vuông góc BC . Tính AB,OA biết R=1,5 và BC=24
c, CM: BC là phân giác góc ABH
d, I là giao điểm AD và BH , BD giao AC tại E . CM : IH=IB