Cho pt : x2−6x−7−m0x2−6x−7−m0. Xác định m để pt có nghiệm thuộc D(−∞;0)∪(7;+∞)
Đọc tiếp
Cho pt : x2−6x−7−m=0x2−6x−7−m=0. Xác định m để pt có nghiệm thuộc D=(−∞;0)∪(7;+∞)
Những câu hỏi liên quan
Cho pt (m+1)x2-2(m-1)x+m-20a, Xác định m để pt có 2 nghiệm phân biệtb, Xác định m để pt có một nghiệm bằng 2. Tìm nghiệm kiac, Xác định m để pt có 2 nghiệm x1; x2 thỏa mãn 1/x1 + 1/x2 7/4; 1/x1 + 1/x2 1; x12+x222d, Xác định m để pt có 2 nghiệm thỏa mãn 3(x1+x2)5x1x2
Đọc tiếp
Cho pt (m+1)x2-2(m-1)x+m-2=0
a, Xác định m để pt có 2 nghiệm phân biệt
b, Xác định m để pt có một nghiệm bằng 2. Tìm nghiệm kia
c, Xác định m để pt có 2 nghiệm x1; x2 thỏa mãn 1/x1 + 1/x2 = 7/4; 1/x1 + 1/x2 = 1; x12+x22=2
d, Xác định m để pt có 2 nghiệm thỏa mãn 3(x1+x2)=5x1x2
Cho pt : \(x^2-6x-7-m=0\). Xác dịnh m để pt có nghiệm thuộc \(D=\left(-\infty;0\right)\cup\left(7;+\infty\right)\)
Cho pt : x^-6x+m-3=0. Tìm m để pt có 2 nghiệm phân biệt thoả mãn: (x1-1)*(x2^-5x2+m-4)=0
(x1-1)(x2^2-5x2+m-4)=0
=>x1=1 và x2^2-x2(x1+x2-1)+x1x2+1=0
=>x1=1 và x2^2-x2x1-x2^2+x2+x1x2+1=0
=>x1=1 và x2=-1
x1*x2=m-3
=>m-3=-1
=>m=2
Đúng 0
Bình luận (0)
20 tháng 3 2022 lúc 15:42
cho PT x2−2(m−1)x−m=0x2−2(m−1)x−m=0
a) tìm hệ thức liên hệ giữa 2 nghiệm không phụ thuộc vào m
b) tìm m để Pt có đúng 1 nghiệm âm
c) tìm m để PT có 2 nghiệm = nhau về giá trị tuyệt đối và trái dấu nhau
d) tìm m để |x1−x2|nhỏnhất
Xác định m để pt có 2 nghiệm x1,x2 thỏa mãn ĐK kèm theo:
x2 - (m + 2)x + 2 = 0 ( \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{9}{2}\))
Tìm giá trị của tham số m để pt x2 - 2(m+2)x + m2 + 4 = 0 có 2 nghiệm x1,x2 thỏa mãn hệ thức x1 + 2x2 = 7
Bước 1: Tìm điều kiện của tham số để phương trình có hai nghiệm phân biệt.
Bước 2: Khi phương trình đã có hai nghiệm phân biệt, ta áp dụng Vi-ét để tìm các giá trị của tham số.
Bước 3. Đối chiếu với điều kiện và kết luận bài toán.
xem tr sách của anh
Đúng 0
Bình luận (0)
Bài 1:
PT có 2 nghiệm \(\Leftrightarrow\Delta=\left(m+2\right)^2-4\cdot2\ge0\Leftrightarrow m^2+4m-8\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-2-2\sqrt{3}\\m\ge-2+2\sqrt{3}\end{matrix}\right.\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=2\end{matrix}\right.\)
Ta có \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{9}{2}\Leftrightarrow2\left(x_1^2+x_2^2\right)=9x_1x_2\)
\(\Leftrightarrow2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=18\\ \Leftrightarrow2\left(m+2\right)^2-8=18\\ \Leftrightarrow2m^2+8m+8-8=18\\ \Leftrightarrow m^2+4m-9=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-2+\sqrt{13}\\m=-2-\sqrt{13}\end{matrix}\right.\left(tm\right)\)
Đúng 1
Bình luận (11)
cho pt :
\(2x^2-6x+m+7=0\)
a. giải pt vs m =3
b. voi gt nào của m thì pt có một trong các nghiệm = -4
c. tìm m để pt có 2 nghiệm x1 và x2 thỏa mãn đk x1=-2x2
a) với m=3 phương trình đã cho có dạng
\(2x^2-6x+3+7=0\Leftrightarrow2x^2-6x+10=0\Leftrightarrow x^2-3x+5=0\circledast\)
ta có△=\(\left(-3\right)^2+4.1.5=-11< 0\)
⇒ phương trình \(\circledast\) vô nghiệm
Vậy phương trình đã cho vô nghiệm với m=3
b)phương trình có một nghiệm bằng -4
\(2.\left(-4\right)^2-6.\left(-4\right)+m+7=0\Leftrightarrow32+24+m+7=0\Leftrightarrow63+m=0\Leftrightarrow m=-63\)
Vậy m=-63 là giá trị cần tìm
Đúng 0
Bình luận (2)
cho pt : x^2-2left(m+1right)x+2m+100a) Giải và biện luận về số nghiệm của ptb) Trong trường hợp pt có 2 nghiệm phân biệt là x1; x2; hãy tìm 1 hệ thức liên hệ giữa x1; x2 mà ko phụ thuộc vào mc) Tìm giá trị của m để P10x_1x_2+x_1^2+x_2^2đạt GTNNd) Xác định m để pt có 2 nghiệm phân biệt âm e) Xác định m để PT có 2 nghiệm trái dấu
Đọc tiếp
cho pt : \(x^2-2\left(m+1\right)x+2m+10=0\)
a) Giải và biện luận về số nghiệm của pt
b) Trong trường hợp pt có 2 nghiệm phân biệt là x1; x2; hãy tìm 1 hệ thức liên hệ giữa x1; x2 mà ko phụ thuộc vào m
c) Tìm giá trị của m để \(P=10x_1x_2+x_1^2+x_2^2\)đạt GTNN
d) Xác định m để pt có 2 nghiệm phân biệt âm
e) Xác định m để PT có 2 nghiệm trái dấu
xác định m để pt sau có nghiệm x=2
mx^3-2x^2x^2+6x+6x+m^2+4=0
mik làm mà ko hiểu@@@
-sad nặng-
![❄Đờ[̲̅i̲̅]❤Là❤Bể❤K[̲̅h̲̅...](https://hoc24.vn/images/avt/avt2782456_256by256.jpg)
Càng đọc đề càng khó hiểu, ghi lại cho rõ hơn được không??
Đúng 0
Bình luận (0)
Dạng này chỉ cần thay x vào phương trình rồi giải phương trình tìm m là xong.
Bạn làm luôn thực hành đi :)
Đúng 0
Bình luận (0)
Xác định m để phương trình
m
x
2
-
6
x
-
7
có 4 nghiệm phân biệt. A. m ∈ (−16; 16). B. m ∈ (0; 16) C. m ∈ ∅. D. m ∈ [0; 16].
Đọc tiếp
Xác định m để phương trình m = x 2 - 6 x - 7 có 4 nghiệm phân biệt.
A. m ∈ (−16; 16).
B. m ∈ (0; 16)
C. m ∈ ∅.
D. m ∈ [0; 16].
m = x 2 - 6 x - 7 là phương trình hoành độ giao điểm của đường thẳng y = m và đồ thị (C): y = x 2 - 6 x - 7
Vẽ (P): y = x 2 - 6 x - 7 , lấy đối xứng phần phía dưới Ox của (P) lên trên Ox và xóa đi phần phía dưới Ox (vì y = x 2 - 6 x - 7 , ∀ x ∈ R ), ta được đồ thị (C).
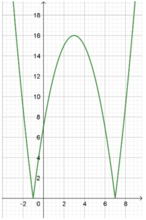
Dựa vào đồ thị: phương trình m = x 2 - 6 x - 7 có 4 nghiệm phân biệt khi m ∈ 0 ; 16 .
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
giải giùm e câu c vs ạ
c4
cho pt ẩn x: x2−2x−m2−4=0x2−2x−m2−4=0(1)
a/ giải pt đã cho khi m=1212
b/ chứng minh pt luôn có 2 nghiệm phân biệt vs mọi m
c/ tính giá trị của m để pt (1) có 2 nghiệm x1,x2 sao cho 2x1,x2(2-3x1)=2
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ bên trái khung soạn thảo) để được hỗ trợ tốt hơn.
Đúng 2
Bình luận (0)