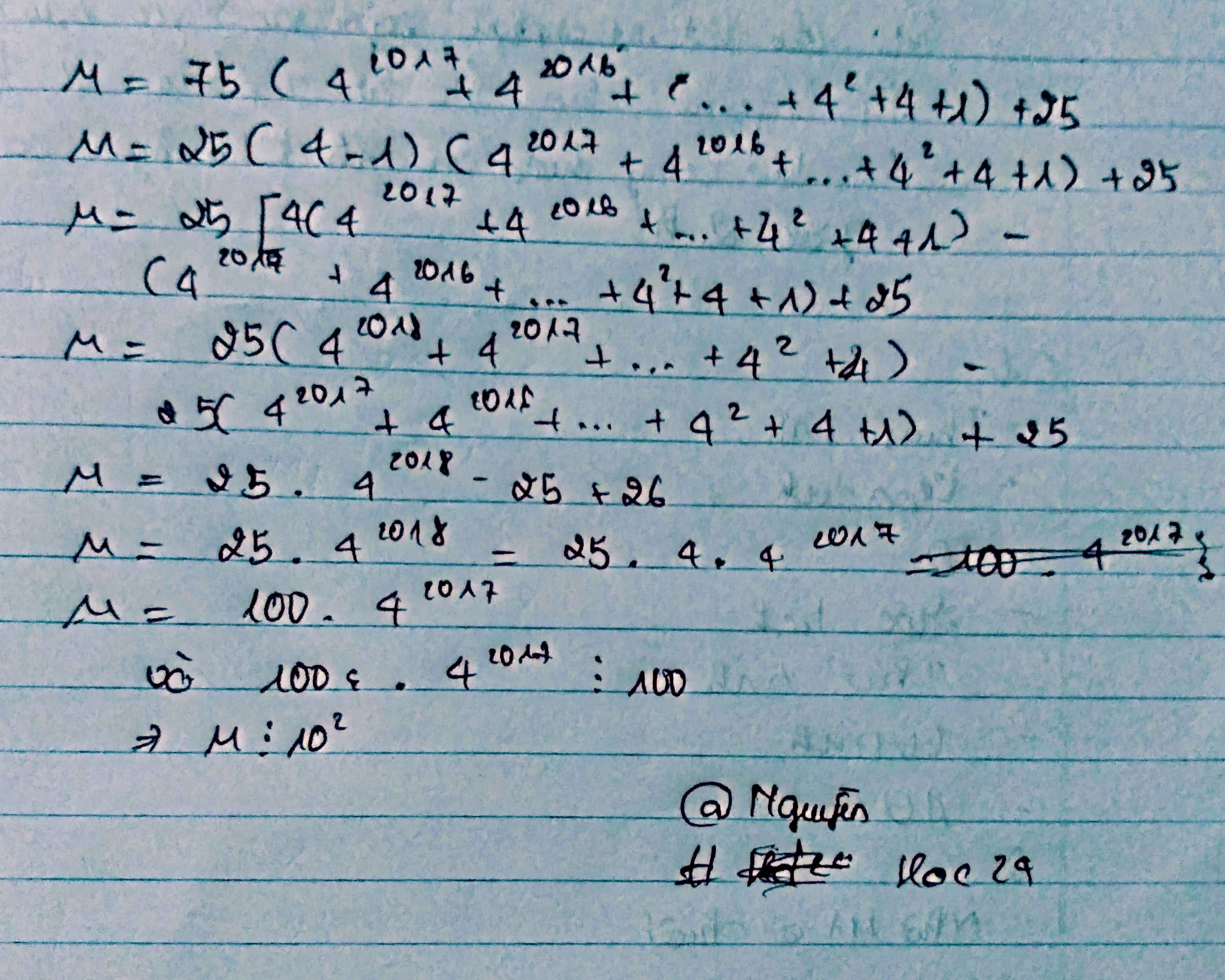Chứng tỏ rằng : A = 75.(42013 + 42012 + .... + 42 + 5) + 25 chia hết cho 42014

Những câu hỏi liên quan
Chứng tỏ rằng :
A = 75 . ( 42004 + 42003 + ...... + 42 + 4 + 1 ) + 25 là số chia hết cho 100
A, Chứng tỏ rằng: M = 75.(42017+ 42016 +42 +4 + 1) +25 chia hết cho 10² 6+.
2. Chứng tỏ rằng M=75.(42021+42020+....+42+4+1)+ 25 chia hết cho 100
\(M=75.4\left(4^{2020}+4^{2019}+...+4+1\right)+75+25=\)
\(=300.\left(4^{2020}+4^{2019}+...+4+1\right)+100=\)
\(=100\left[3.\left(4^{2020}+4^{2019}+...+4+1\right)+1\right]⋮100\)
Đúng 1
Bình luận (0)
Cho A = 75 x (42023 + 42022 + ... + 42 + 5) + 25. Chứng minh rằng A chia hết cho 42024.
Thị Hạnh Nguyễn đây là chỗ học tập ko phải để bn gửi mấy cái linh tinh này nhé nếu bn còn như vậy thì mình sẽ tố cáo bn với admin OLM nha
Đúng 0
Bình luận (0)
A = 75 x ( 42023 + 42022 +.....+ 42 + 5) + 25
A = 75 x ( 42023 + 42022 +.....+ 42) + 75 x 5 + 25
A = 75 x ( 42023 + 42022 +......+ 42) + 400
Đặt B = 42023 + 42022 +.....+43 + 42
4 x B = 42024 + 42023 + 42022+.....+43
4 x B - B = 42024 - 42
3 x B = 42024 - 42
B = \(\dfrac{4^{2024}-4^2}{3}\)
A = 75 x \(\dfrac{4^{2024}-4^2}{3}\) + 400
A = 25 x ( 42024 - 16) + 400
A = 25 x 42024 - 400 + 400
A = 25 x 42024
4 2024 ⋮ 42024 ⇒ 25 x 42024 ⋮ 42024
⇒ A = 75 x ( 42023 + 42022+ ....+ 42+5) +25 ⋮ 42024 (đpcm)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
chứng tỏ rằng: A=75 x (4^2013+4^2012+...+4^2+5)+ 25 chia hết cho 4^2014
chứng tỏ rằng e=75.(5+4^2+4^3+...+4^2021)+25 chia hết cho 4^2022
nhanh chữa cho mình mình đang vội
\(E=25\left[3\cdot\left(5+4^2+4^3+...+4^{2021}\right)+1\right]\)
\(=25\cdot\left(4^2+4^2+4^3+...+4^{2021}\right)\)
\(=25\cdot4^{2022}⋮4^{2022}\)
Đúng 1
Bình luận (0)
Chứng tỏ rằng A= 75( 4^2023+ 4^2022+4^2021+...+ 4^2+ 4+ 1)+ 25 chia hết cho 100
Đặt \(A=75\left(4^{2023}+4^{2022}+...+4^2+4+1\right)+25\)
Đặt \(B=4^{2023}+4^{2022}+...+4^2+4+1\)
=>\(4B=4^{2024}+4^{2023}+...+4^3+4^2+4\)
=>\(4B-B=4^{2024}+4^{2023}+...+4^3+4^2+4-4^{2023}-4^{2022}-...-4^2-4-1\)
=>\(3B=4^{2024}-1\)
=>\(B=\dfrac{4^{2024}-1}{3}\)
\(A=75\left(4^{2023}+4^{2022}+...+4^2+4+1\right)+25\)
\(=75\cdot\dfrac{4^{2024}-1}{3}+25\)
\(=25\cdot\left(4^{2024}-1\right)+25\)
\(=25\cdot4^{2024}\)
\(=25\cdot4\cdot4^{2023}=100\cdot4^{2023}⋮100\)
Đúng 0
Bình luận (0)
Chứng tỏ rằng \(M=75.\left(4^{2017}+4^{2016}+...+4^2+4+1\right)+25\) chia hết cho 102
a) Cho P 1 + 3 + 32 + 33 +.......+ 3101. Chứng tỏ rằng P⋮13.
b) Cho B 1 + 22 + 24 +.......+ 22020. Chứng tỏ rằng B ⋮ 21.
c) Cho A 2 + 22 + 23 +........+ 220. Chứng tỏ A chia hết cho 5.
d) Cho A 1 + 4 + 42 + 43 +..........+ 498. Chứng tỏ A chia hết cho 21.
e) Cho A 119 + 118 + 117 +.........+ 11 + 1. Chứng tỏ A chia hết cho 5.
Đọc tiếp
a) Cho P = 1 + 3 + 32 + 33 +.......+ 3101. Chứng tỏ rằng P⋮13.
b) Cho B = 1 + 22 + 24 +.......+ 22020. Chứng tỏ rằng B ⋮ 21.
c) Cho A = 2 + 22 + 23 +........+ 220. Chứng tỏ A chia hết cho 5.
d) Cho A = 1 + 4 + 42 + 43 +..........+ 498. Chứng tỏ A chia hết cho 21.
e) Cho A = 119 + 118 + 117 +.........+ 11 + 1. Chứng tỏ A chia hết cho 5.
a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5
Đúng 0
Bình luận (0)