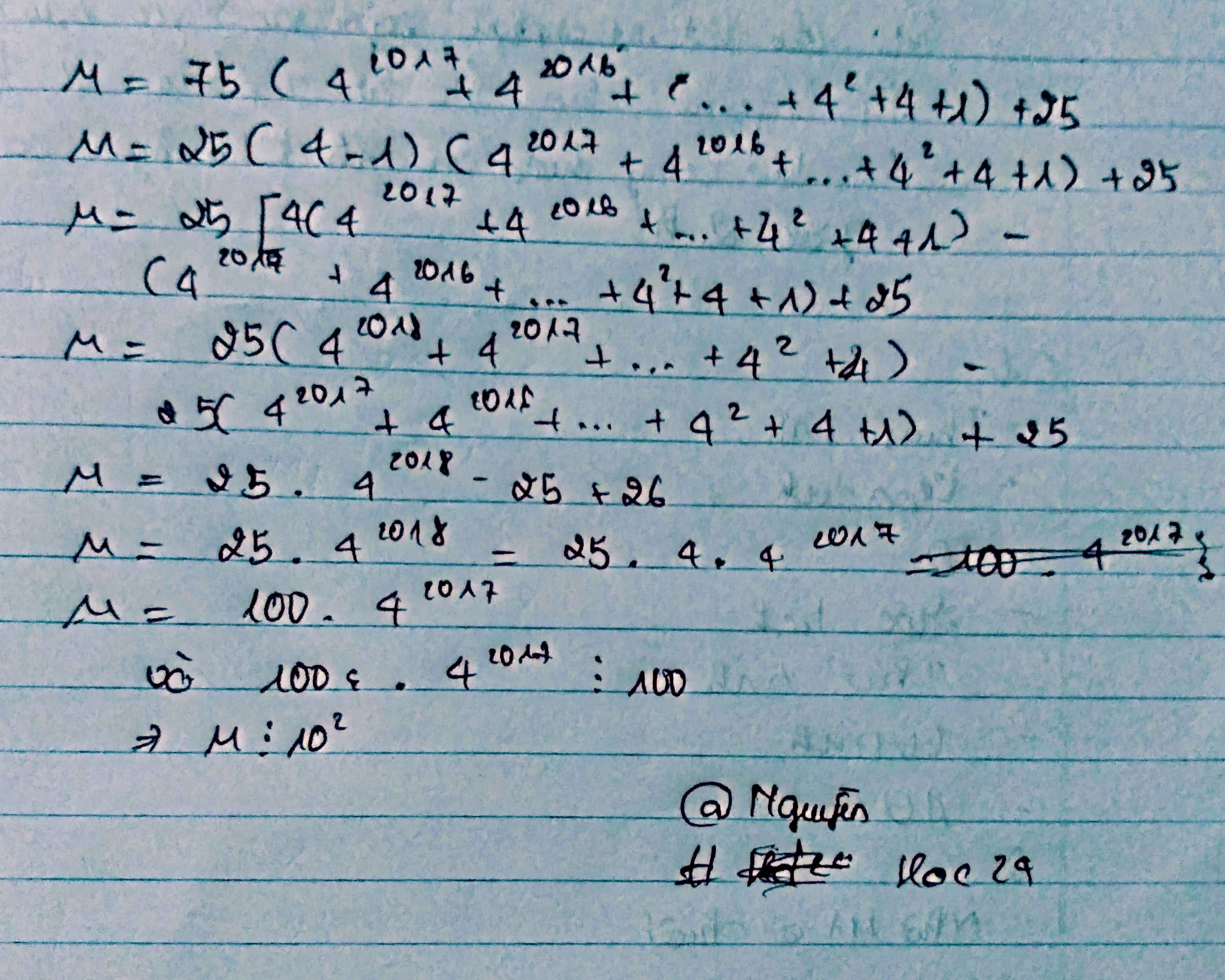Các câu hỏi tương tự
Chứng tỏ rằng:
\(A=75.\left(4^{2004}+4^{2003}+...+4^2+4+1\right)+25\)là số chia hết cho 100
a)chứng tỏ rằng M=75*(4^2017+4^2016+...+4^2+4+1)chia hết cho 10^2
b)cho tích a*b là số chính phương và (a,b)=1 cmr a và b đều là số chính phương
Chứng tỏ rằng:
A = \(75\times\left(4^{2004}+4^{2003}+...+4^2+4+1\right)+25\)chia hết cho 100.
cm \(75\cdot\left(1+4+4^2+....+4^{2016}\right)+25\) chia hết cho\(4^{2017}\)
Chứng tỏ rằng
\(A=75\left(4^{2004}+4^{2003}+...+4^2+4+1\right)\)Là số chia hết hết cho 100
Chứng tỏ rằng A= 75( 4^2023+ 4^2022+4^2021+...+ 4^2+ 4+ 1)+ 25 chia hết cho 100
1. Chứng tỏ rằng : A= 75.(42004+ 42003+42+4+1)+25 là số chia hết cho 100
2. Tìm n biết \(\left(\frac{1}{3}\right)^{2n-1}=3^5\)
ai biết thì jup nha. Thanks nhìu
CMR biểu thức A=75.(4^2017+4^2016+..+4^2+5)+25 chia hết cho 4^2018
A, Chứng tỏ rằng: M = 75.(42017+ 42016 +42 +4 + 1) +25 chia hết cho 10² 6+.