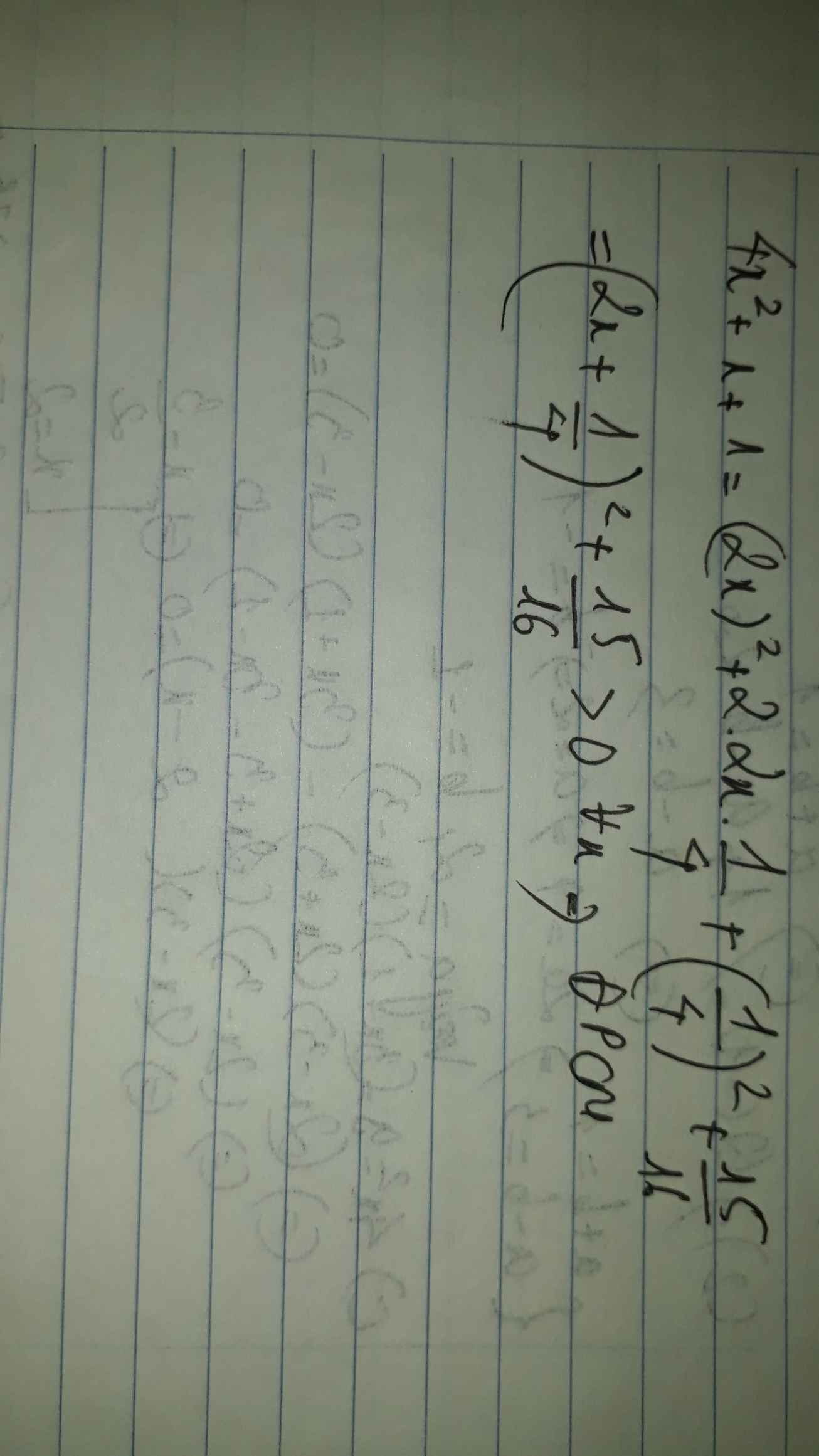Cho đa thức chứng minh:X^2+x+1>0 với mọi số thực x

Những câu hỏi liên quan
a, Tìm a để đa thức \(2x^3-3x^2 x a\) chia hết cho đa thức x 2
b, Chứng minh x - x^2 - 1 < 0 với mọi số thực x
Xem chi tiết
a)(6x mũ 2+13x-5)
b)(6x+1)mũ 2 + (6x-1)mũ 2-2(1+6x)(6x-1)
c)Chứng minh:x mũ 2-2x +3 ≥ 2 với mọi số thực x
a)chứng minh rằng x-x^2-1<0 với mọi số thực x
b)tìm gtnn của đa thức sau:f(x)=x^2-4x+9
\(-x^2+x-1=--\left(x^2-x+\frac{1}{4}\right)-\frac{3}{4}=-\left(x-\frac{1}{2}\right)^2-\frac{3}{4}< 0\)
\(f\left(x\right)=x^2-4x+4+5=\left(x-2\right)^2+5\ge5\)
\(f\left(x\right)_{min}=5\) khi \(x=2\)
Chứng tỏ rằng đa thức A( x ) = 0 - x^5 + 2 ko có nghiệm với mọi số thực x
Bn cho đa thức A(x) = 0 sau đó tính và viết câu kết luận
mk nghĩ là thế!! =))
a) Tìm số a để đa thức x² + 5x + a chia hết cho đa thức x - 1
b) Chứng minh rằng: x² – x + 1 > 0 với mọi số thực x?
c) Tìm giá trị nhỏ nhất của biểu thức A = x² – 6x + 11
d) Tìm giá trị lớn nhất của biểu thức B = – x² + 4x – 5
b: \(x^2-x+1=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)
c: \(A=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)
Dấu '=' xảy ra khi x=3
d: \(B=-\left(x^2-4x+5\right)=-\left(x^2-4x+4+1\right)=-\left(x-2\right)^2-1\le-1\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 0
Bình luận (0)
a,Cho đa thức f(x)=ax+b (a khác 0). Biết f(0)=0, chứng minh rằng F(x)=-f(-x)với mọi x
b,Đa thức f(x)=ax^2=bx+c (a khác 0).Biết F(1)=F(-1), chứng minh rằng f(x) với mọi x
Câu1
A. tìm a để đa thức 3x^3+2x^2-7x-a chia hết cho đa thức 3x-1
B. Chứng minh rằng x-x^2-1 <0 với mọi số thực x
C. Tìm giá trị nhỉ nhất của biểu thức p(x) =x^2-5x
D .tìm gia tri nho nhat cua da thuc sau f (x)=x^2-4x+9
a: \(\Leftrightarrow3x^3-x^2+3x^2-x-6x+2-a-2⋮3x-1\)
=>-a-2=0
hay a=-2
b: \(-x^2+x-1\)
\(=-\left(x^2-x+1\right)\)
\(=-\left(x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}< 0\forall x\)
c: \(P\left(x\right)=x^2-5x+\dfrac{25}{4}-\dfrac{25}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{25}{4}\ge-\dfrac{25}{4}\forall x\)
Dấu '=' xảy ra khi x=5/2
d: \(f\left(x\right)=x^2-4x+4+5=\left(x-2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi x=2
Đúng 0
Bình luận (0)
cho đa thức P(x)=ax^3+bx^2+cx+d thỏa mãn P(0)=1 và P(x+1) - P(x)=x^2 với mọi số thực x, tìm a,b,c d
chứng minh biểu thức 4\(x^2\) + x + 1 > 0 với mọi số thực x
\(4x^2+x+1=3x^2+x^2+x+\dfrac{1}{4}+\dfrac{3}{4}=3x^2+\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\in R\)
Đúng 1
Bình luận (0)
Ta có: \(4x^2+x+1\)
\(=\left(2x\right)^2+2\cdot2x\cdot\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{15}{16}\)
\(=\left(2x+\dfrac{1}{4}\right)^2+\dfrac{15}{16}>0\forall x\)
Đúng 1
Bình luận (0)