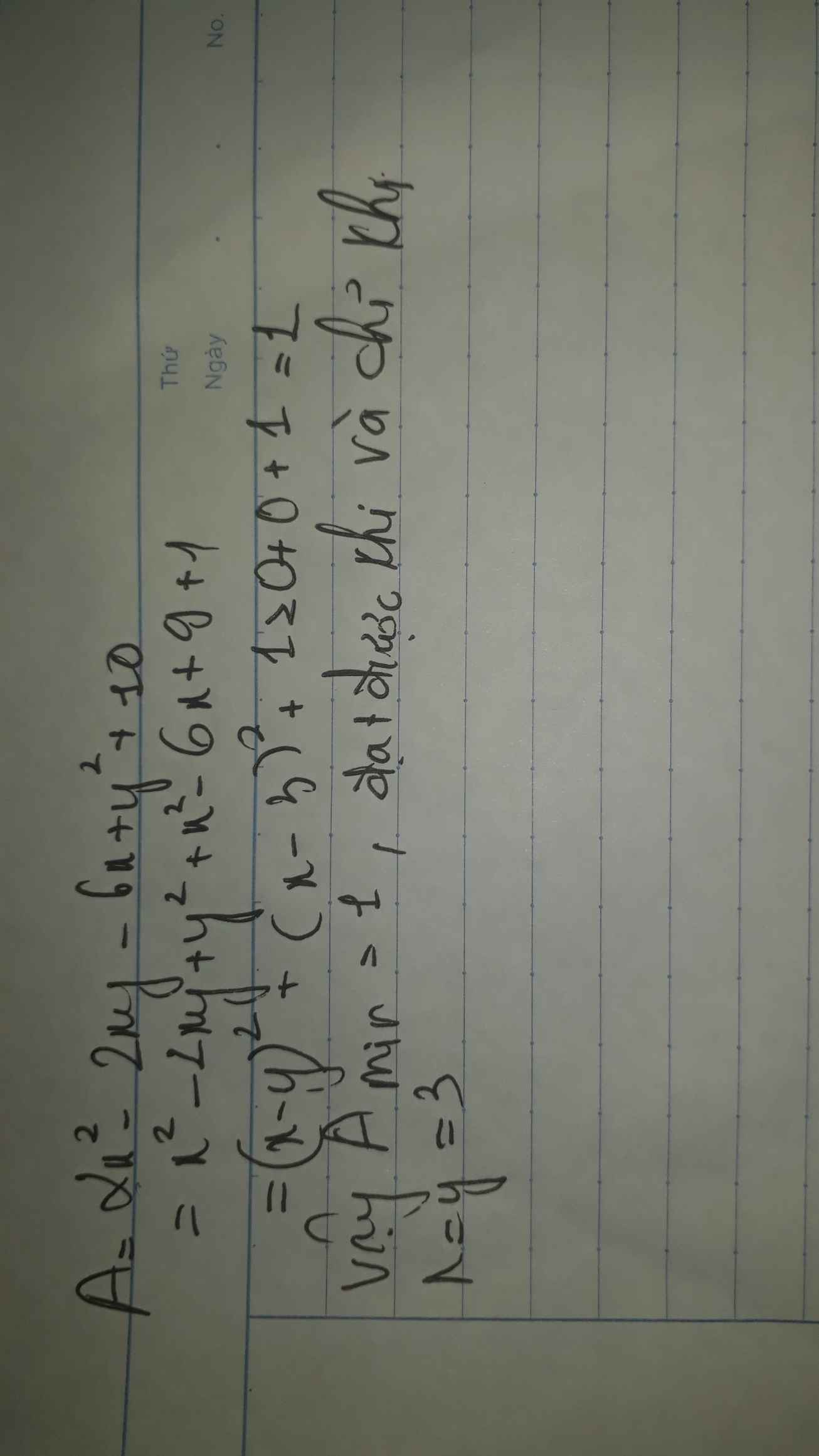A= -x²+2x+3

=>A= -(x²-2x+3)

=>A= -(x²-2.x.1+1+3-1)

=>A=-[(x-1)²+2]

=>A= -(x+1)²-2

Vì -(x+1)² ≤0=> A≤-2

Dấu "=" xảy ra khi

-(x+1)²=0 => x=-1

Vây A lớn nhất= -2 khi x= -1

B=x²-2x+4y²-4y+8

=> B= (x²-2x+1)+(4y²-4y+1)+6

=> B=(x-1)²+(2y+1)²+6

=> B lớn nhất=6 khi x=1 và y=-1/2

`A=2x^2-2xy-6x+y^2+10`

`A=x^2-2xy+y^2+x^2-6x+10`

`A=(x-y)^2+x^2-6x+9+1`

`A=(x-y)^2+(x-3)^2+1`

Vì `(x-y)^2+(x-3)^2>=0=>A>=1`

Dấu "=" xảy ra khi `{(x-y=0),(x-3=0):}<=>x=y=3`

A=\(\left(x^2-2xy+y^2\right)+\left(x^2-6x+9\right)+1=\left(x-y\right)^2+\left(x-3\right)^2+1\ge1\\ \)

dấu= xảy ra khi x=y=3

tick mik nha

\(P=x^2+2y^2+2xy-6x-8y+2024\)

\(P=x^2+y^2+y^2+2xy-6x-6y-2y+2024\)

\(P=\left(x^2+2xy+y^2\right)-\left(6x+6y\right)+9+y^2-2y+1+2014\)

\(P=\left(x+y\right)^2-2\left(x+y\right)3+3^2+\left(y^2-2y+1\right)+2014\)

\(P=\left(x+y-3\right)^2+\left(y-1\right)^2+2014\)

\(P\ge2014\forall x;y\)

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x+y-3=0\\y-1=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=1\end{cases}}}\)

Vậy.....

Lời giải:
$2x^2+y^2+2xy-6x-2y=8$

$\Leftrightarrow (x^2+y^2+2xy)+x^2-6x-2y=8$
$\Leftrightarrow (x+y)^2-2(x+y)+x^2-4x=8$

$\Leftrightarrow (x+y)^2-2(x+y)+1+(x^2-4x+4)=13$

$\Leftrightarrow (x+y-1)^2+(x-2)^2=13$
$\Rightarrow (x-2)^2=13-(x+y-1)^2\leq 13$
Mà $(x-2)^2$ là scp với mọi $x$ nguyên nên $(x-2)^2\in\left\{0; 1; 4; 9\right\}$

Nếu $(x-2)^2=0\Rightarrow (x+y-1)^2=13-(x-2)^2=13$ (không là scp - loại) 

Nếu $(x-2)^2=1\Rightarrow (x+y-1)^2=12$ (không là scp - loại)

Nếu $(x-2)^2=4\Rightarrow (x+y-1)^2=9$

$\Rightarrow x-2=\pm 2$ và $x+y-1=\pm 3$
TH1: $x-2=2; x+y-1=3\Rightarrow x=4; y=0$

TH2: $x-2=2; x+y-1=-3\Rightarrow x=4; y=-6$

TH3: $x-2=-2; x+y-1=3\Rightarrow x=0; y=4$

TH4: $x-2=-2; x+y-1=-3\Rightarrow x=0; y=-2$

Nếu $(x-2)^=9\Rightarrow (x+y-1)^2=4$ (bạn cũng làm tương tự trên)

\(A=2x^2+y^2-2x+2xy+2y+3=y^2+2y\left(x+1\right)+\left(x+1\right)^2+\left(x^2-4x+4\right)-2=\left(y+x+1\right)^2+\left(x-2\right)^2-2\ge-2\)

\(minA=-2\Leftrightarrow\)\(\left\{{}\begin{matrix}x=2\\y=-3\end{matrix}\right.\)

\(P=x^3+2021xy+y^3\)

\(=\left(x+y\right)^3-3xy\left(x+y\right)+2021xy\)

\(=\left(\dfrac{2021}{3}\right)^3\)

\(=\dfrac{8254655261}{27}\)

A= 2x^2 + y^2 - 2xy -2x+3

A= x^2-2xy + y^2 + x^2 - 2x+ 1 +2

A= (x-y)^2 + (x-1)^2 + 2

(x-y)^2> hoặc = 0 với mọi giá trị của x

(x-1)^2 > hoặc =0 với mọi giá trị của x

=> (x-y)^2 + (x-1)^2 > hoặc =0 với mọi giá trị của x

=> (x-y)^2 + (x-1)^2 + 2 > hoặc =2

=> A lớn hơn hoặc bằng 2

=> GTNN của A=2 tại x=y=1

a: \(P=x^2+y^2-6x-2y+17\)

\(=x^2-6x+9+y^2-2y+1+7\)

\(=\left(x-3\right)^2+\left(y-1\right)^2+7\ge7\forall x,y\)

Dấu '=' xảy ra khi x-3=0 và y-1=0

=>x=3 và y=1

b: \(Q=x^2+xy+y^2-3x-3y+999\)

\(=x^2+x\left(y-3\right)+y^2-3y+999\)

\(=x^2+2\cdot x\cdot\left(\frac12y-\frac32\right)+\left(\frac12y-\frac32\right)^2+y^2-3y-\left(\frac12y-\frac32\right)^2+999\)

\(=\left(x+\frac12y-\frac32\right)^2+y^2-3y-\left(\frac14y^2-\frac32y+\frac94\right)+999\)

\(=\left(x+\frac12y-\frac32\right)^2+\frac34y^2-\frac32y-\frac94+999\)

\(=\left(x+\frac12y-\frac32\right)^2+\frac34\left(y^2-2y-3\right)+999\)

\(=\left(x+\frac12y-\frac32\right)^2+\frac34\left(y^2-2y+1-4\right)+999\)

\(=\left(x+\frac12y-\frac32\right)^2+\frac34\left(y-1\right)^2+996\ge996\forall x,y\)

Dấu '=' xảy ra khi \(\begin{cases}y-1=0\\ x+\frac12y-\frac32=0\end{cases}\Rightarrow\begin{cases}y=1\\ x=-\frac12y+\frac32=-\frac12+\frac32=\frac22=1\end{cases}\)

c: \(R=2x^2+2xy_{}+y^2-2x+2y+15\)

\(=x^2-4x+4+x^2+2xy+y^2+2x+2y+11\)

\(=\left(x-2\right)^2+x^2+2xy+y^2+2x+2y+1+10\)

\(=\left(x-2\right)^2+\left(x+y+1\right)^2+10\ge10\forall x,y\)

Dấu '=' xảy ra khi \(\begin{cases}x-2=0\\ x+y+1=0\end{cases}\Rightarrow\begin{cases}x=2\\ y=-x-1=-2-1=-3\end{cases}\)

d: \(S=x^2+26y^2-10xy+14x-76y+59\)

\(=x^2-10xy+25y^2+14x-70y+y^2-6y+59\)

\(=\left(x-5y\right)^2+14\left(x-5y\right)+49+y^2-6y+9+1\)

\(=\left(x-5y+7\right)^2+\left(y-3\right)^2+1\ge1\forall x,y\)

Dấu '=' xảy ra khi \(\begin{cases}y-3=0\\ x-5y+7=0\end{cases}\Rightarrow\begin{cases}y=3\\ x=5y-7=5\cdot3-7=15-7=8\end{cases}\)

e: \(T=x^2-4xy+5y^2+10x-22y+28\)

\(=x^2-4xy+4y^2+10x-20y+y^2-2y+28\)

\(=\left(x-2y\right)^2+10\left(x-2y\right)+25+y^2-2y+1+2\)

\(=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\forall x,y\)

Dấu '=' xảy ra khi \(\begin{cases}y-1=0\\ x-2y+5=0\end{cases}\Rightarrow\begin{cases}y=1\\ x=2y-5=2\cdot1-5=2-5=-3\end{cases}\)