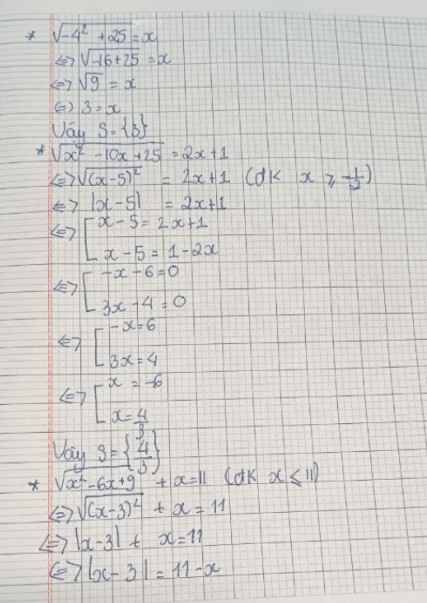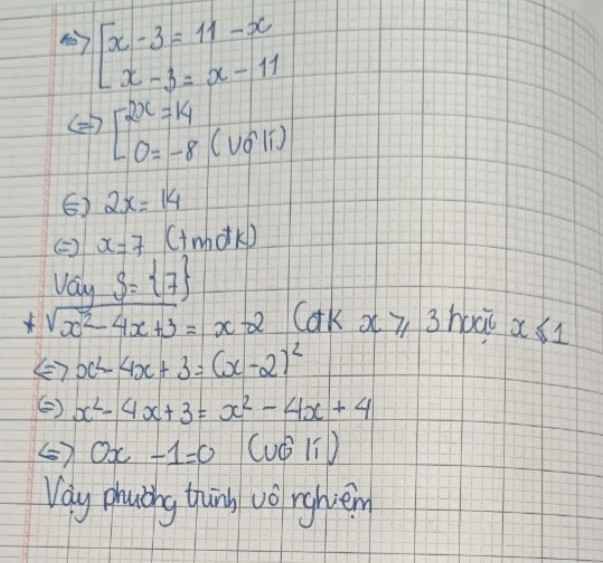Giải phương trình: 2x - \(\sqrt{25-10x+x^2}\) =4
Những câu hỏi liên quan
10 tháng 7 2021 lúc 20:47
Giải phương trình
a) \(\sqrt{x-2\sqrt{x-1}}-\sqrt{x-1}=1\)
b)\(\sqrt{x^4++2x^2+1}=\sqrt{x^2+10x+25}-10x+22\)
a) Ta có: \(\sqrt{x-2\sqrt{x-1}}-\sqrt{x-1}=1\)
\(\Leftrightarrow\left|\sqrt{x-1}-1\right|=\sqrt{x-1}+1\)
\(\Leftrightarrow\sqrt{x-1}=\sqrt{x-1}+1+1\)(Vô lý)
Vậy: \(S=\varnothing\)
b) Ta có: \(\sqrt{x^4+2x^2+1}=\sqrt{x^2+10x+25}-10x+22\)
\(\Leftrightarrow x^2+1=\left|x+5\right|-10x+22\)
\(\Leftrightarrow\left|x+5\right|=x^2+1+10x-22=x^2+10x-21\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=x^2+10x-21\left(x\ge-5\right)\\-x-5=x^2+10x-21\left(x< -5\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+10x-21-x-5=0\\x^2+10x-21+x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2+9x-26=0\\x^2+11x-16=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-9+\sqrt{185}}{2}\\x=\dfrac{-11-\sqrt{185}}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
13 tháng 9 2023 lúc 20:53
Bài tập:Giải các phương trình sau
1)\(\sqrt{-4^2+25}=x\)
2)\(\sqrt{x^2-10x+25}\)=2x+1
3)\(\sqrt{x^2-6x+9}+x=11\)
4)\(\sqrt{x^2-4x+3}=x-2\)
1. Giải phương trình:1/ sqrt{x-4}+sqrt{6-x}x^2-10x+272/ sqrt{x^2-6x+9}+sqrt{x^2-10x+25}83/ y^2-2y+3dfrac{6}{x^2+2x+4}4/ x^2-x-42sqrt{x-1}left(1-xright)5/ x^2-left(m+1right)x+2m-606/ 615+x^22^y2.a, Cho các số dương a,b thoả mãn a+b2ab.Tính GTLN của biểu thức Qdfrac{2}{sqrt{a^2+b^2}}.b, Cho các số thực x,y thoả mãn x-sqrt{y+6}sqrt{x+6}-y.Tính GTNN và GTLN của biểu thức Px+y.3. Cho hàm số yleft(m+3right)x+2m-10 có đồ thị đường thẳng (d), hàm số yleft(m-4right)x-2m-8 có đồ thị đường thẳng (d2) (m là...
Đọc tiếp
1. Giải phương trình:
1/ \(\sqrt{x-4}+\sqrt{6-x}=x^2-10x+27\)
2/ \(\sqrt{x^2-6x+9}+\sqrt{x^2-10x+25}=8\)
3/ \(y^2-2y+3=\dfrac{6}{x^2+2x+4}\)
4/ \(x^2-x-4=2\sqrt{x-1}\left(1-x\right)\)
5/ \(x^2-\left(m+1\right)x+2m-6=0\)
6/ \(615+x^2=2^y\)
2.
a, Cho các số dương a,b thoả mãn \(a+b=2ab\).
Tính GTLN của biểu thức \(Q=\dfrac{2}{\sqrt{a^2+b^2}}\).
b, Cho các số thực x,y thoả mãn \(x-\sqrt{y+6}=\sqrt{x+6}-y\).
Tính GTNN và GTLN của biểu thức \(P=x+y\).
3. Cho hàm số \(y=\left(m+3\right)x+2m-10\) có đồ thị đường thẳng (d), hàm số \(y=\left(m-4\right)x-2m-8\) có đồ thị đường thẳng (d2) (m là tham số, \(m\ne-3\) và \(m\ne4\)). Trên mặt phẳng toạ độ Oxy, (d) cắt trục hoành tại điểm A, (d2) cắt trục hoành tại điểm B, (d) cắt (d2) tại điểm C nằm trên trục tung. Chứng minh hệ thức \(\dfrac{OA}{BC}=\dfrac{OB}{AC}\).
4. Cho 2 đường tròn (O) và (I) cắt nhau tại dây AB, chứng minh rằng \(\Delta OAI=\Delta OBI\).
giải phương trình
\(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
ĐKXĐ: \(x\in R\)
\(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
=>\(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}+x^2+2x-4=0\)
\(\Leftrightarrow\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}+x^2+2x+1-5=0\)
=>\(\sqrt{3x^2+6x+7}-2+\sqrt{5x^2+10x+14}-3+\left(x+1\right)^2=0\)
=>\(\dfrac{3x^2+6x+7-4}{\sqrt{3x^2+6x+7}+2}+\dfrac{5x^2+10x+14-9}{\sqrt{5x^2+10x+14}+3}+\left(x+1\right)^2=0\)
=>
\(\dfrac{3x^2+6x+3}{\sqrt{3x^2+6x+7}+2}+\dfrac{5x^2+10x+5}{\sqrt{5x^2+10x+14}+3}+\left(x+1\right)^2=0\)
=>\(\dfrac{3\left(x^2+2x+1\right)}{\sqrt{3x^2+6x+7}+2}+\dfrac{5\left(x^2+2x+1\right)}{\sqrt{5x^2+10x+14}+3}+\left(x+1\right)^2=0\)
\(\Leftrightarrow\dfrac{3\left(x+1\right)^2}{\sqrt{3x^2+6x+7}+2}+\dfrac{5\left(x+1\right)^2}{\sqrt{5x^2+10x+14}+3}+\left(x+1\right)^2=0\)
=>\(\left(x+1\right)^2\left(\dfrac{3}{\sqrt{3x^2+6x+7}+2}+\dfrac{5}{\sqrt{5x^2+10x+14}+3}+1\right)=0\)
=>\(\left(x+1\right)^2=0\)
=>x+1=0
=>x=-1(nhận)
Đúng 1
Bình luận (0)
giải các phương trình sau:
a \(\sqrt{3x^2-17x+4}=3x-2\)
b \(2x^2-10x-3\sqrt{x^2-5x+4}+6=0\)
a.
\(\Leftrightarrow\left\{{}\begin{matrix}3x-2\ge0\\3x^2-17x+4=\left(3x-2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\3x^2-17x+4=9x^2-12x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\6x^2+5x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{2}{3}\\\left[{}\begin{matrix}x=0< \dfrac{2}{3}\left(loại\right)\\x=-\dfrac{5}{6}< \dfrac{2}{3}\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy pt đã cho vô nghiệm
Đúng 1
Bình luận (0)
b.
ĐKXĐ: \(\left[{}\begin{matrix}x\ge4\\x\le1\end{matrix}\right.\)
Đặt \(\sqrt{x^2-5x+4}=t\ge0\Leftrightarrow x^2-5x=t^2-4\)
\(\Rightarrow2x^2-10x=2t^2-8\)
Phương trình trở thành:
\(2t^2-8-3t+6=0\)
\(\Leftrightarrow2t^2-3t-2=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-\dfrac{1}{2}< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2-5x+4}=2\)
\(\Leftrightarrow x^2-5x=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải phương trình: \(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
Ta có : \(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}=-x^2-2x+4\)
Trước hết ta xét xem \(f\left(x\right)=-x^2-2x+4\) là hàm số đồng biến hay nghịch biến.Xét \(x_1< x_2< -1\), khi đó : \(f\left(x_1\right)-f\left(x_2\right)=-x_1^2-2x_1+4+x_2^2+2x_2-4=\left(x_2-x_1\right)\left(x_2+x_1+2\right)< 0\)
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\). Vậy f(x) đồng biến với mọi \(x< -1\)
Tương tự ta chứng minh được :
f(x) nghịch biến với mọi x > -1\(f'\left(x\right)=\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}\) đồng biến với mọi x > -1\(f'\left(x\right)=\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}\) nghịch biến với mọi x < -1+ Với x = -1 thì VT = VP => là nghiệm của pt trên
+ Với x < -1 thì do \(f'\left(x\right)\) nghịch biến nên VT > 5 , \(f\left(x\right)\) đồng biến nên VP < 5 => vô lí
+ Với x > -1 thì do \(f'\left(x\right)\) đồng biến nên VT > 5 , \(f\left(x\right)\)nghịch biến nên VP < 5 => vô lí
Vậy x = -1 là nghiệm duy nhất của phương trình.
Đúng 0
Bình luận (0)
Ta có
\(\sqrt{3x^2+6x+7}=\sqrt{3\left(x+1\right)^2+4}\ge2\)
\(\sqrt{5x^2+10x+14}=\sqrt{5\left(x+1\right)^2+9}\ge3\)
4 - 2x - x2 = 5 - (x + 1)2 \(\le5\)
Ta có VT \(\ge5\);VP \(\le\)5
Nên dấu bằng xảy ra khi x = - 1
Đúng 0
Bình luận (0)
Ta có : √3x2+6x+7+√5x2+10x+14=−x2−2x+4
Trước hết ta xét xem ƒ (x)=−x2−2x+4 là hàm số đồng biến hay nghịch biến.Xét x1<x2<−1, khi đó : ƒ (x1)−ƒ (x2)=−x12−2x1+4+x22+2x2−4=(x2−x1)(x2+x1+2)<0
⇒ƒ (x1)<ƒ (x2). Vậy f(x) đồng biến với mọi x<−1
Tương tự ta chứng minh được :
f(x) nghịch biến với mọi x > -1ƒ '(x)=√3x2+6x+7+√5x2+10x+14 đồng biến với mọi x > -1ƒ '(x)=√3x2+6x+7+√5x2+10x+14 nghịch biến với mọi x < -1+ Với x = -1 thì VT = VP => là nghiệm của pt trên
+ Với x < -1 thì do ƒ '(x) nghịch biến nên VT > 5 , ƒ (x) đồng biến nên VP < 5 => vô lí
+ Với x > -1 thì do ƒ '(x) đồng biến nên VT > 5 , ƒ (x)nghịch biến nên VP < 5 => vô lí
Vậy x = -1 là nghiệm duy nhất của phương trình.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải phương trình
a,\(\sqrt{4x^2+20x+25}+\sqrt{x^2-8x+16}=\sqrt{x^2+18x+81}\)
b, \(\sqrt{x^4+2x^2+1}=\sqrt{x^2+10x+25}-10x-22\)
c, \(\sqrt{x+8+2\sqrt{x+7}}+\sqrt{x+8-2\sqrt{x+7}}=4\)
a, \(\sqrt{4x^2+20x+25}\) + \(\sqrt{x^2-8x+16}\) = \(\sqrt{x^2+18x+81}\)
⇔ 4x2 + 20x + 25 + \(2\sqrt{\left(4x^2+20x+25\right)\left(x^2-8x+16\right)}\) = x2 + 18x + 81
⇔ 4x2 + 20x + 25 - x2 - 18x - 81 + \(2\sqrt{\left(2x+5\right)^2.\left(x-4\right)^2}\) = 0
⇔ 3x2 + 2x - 56 + 2.(2x + 5) . (x - 4) = 0
⇔ 3x2 + 2x - 56 + (4x + 10) . (x - 4) = 0
⇔ 3x2 + 2x - 56 + 4x2 - 16x + 10x - 40 = 0
⇔ 7x2 - 4x - 96 = 0
x1 = 4 ( nhận )
x2 = \(\frac{-24}{7}\) ( nhận )
Vậy: S = {4; \(\frac{-24}{7}\)}
Đúng 0
Bình luận (0)
Giải phương trình:
\(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
ta có
zế trái :\(\sqrt{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+9}\ge\sqrt{4}+\sqrt{9}=5\)
zế phải : \(4-2x-x^2=5-\left(x+1\right)^2\le5\)
zậy 2 zế đều = 5 , khi đó x=-1 . Zới giá trị này cả 2 bất đẳng thức này đều trở thành đẳng thức
KL ::
Giải phương trình :\(\sqrt[4]{3x^2+6x+19}+\sqrt{5x^2+10x+14}=4-2x-x^2\)
đề hình như ko có căn bậc 4 chỉ có căn bậc 2 thui
mà căn bậc 4 thì x=-1
Đúng 0
Bình luận (0)