Cho hàm số y=(3m-4)x\(^2\) với m\(\ne\)\(\dfrac{4}{3}\). Tìm các giá trị của tham số m để hàm số :
a) Đạt giá trị lớn nhất là 0
b) Đạt giá trị nhỏ nhất là 0
Cho hàm số y=(3m-4)x\(^2\) với m\(\ne\)\(\dfrac{4}{3}\). Tìm các giá trị của tham số m để hàm số :
a) Đạt giá trị lớn nhất là 0
b) Đạt giá trị nhỏ nhất là 0
a) Để m đạt giá trị lớn nhất là 0 thì \(y=\left(3m-4\right)x^2\le0\) ⇔ \(3m-4\le0\)
⇔ \(m\le\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị lớn nhất là 0 thì \(m< \dfrac{4}{3}\)
b) Để m đạt giá trị nhỏ nhất là 0 thì \(y=\left(3m-4\right)x^2\ge0\) ⇔ \(3m-4\ge0\)
⇔ \(m\ge\dfrac{4}{3}\) nhưng theo điều kiện
thì m ≠ \(\dfrac{4}{3}\)
➤ Để m đạt giá trị nhỏ nhất là 0 thì \(m>\dfrac{4}{3}\)
1) giá trị lớn nhất của hàm số \(y=-\sqrt{x-2}+\sqrt{4-x}\)
2)GTLN của hàm số \(y=\dfrac{1}{4}x^2-x-\sqrt{4x-x^2}\)
đang cần gấp ạ
Câu 1: Cho hàm số y = (3m + 5) x\(^2\) với m \(\ne\) \(\dfrac{-5}{3}\). Tìm các giá trị của tham số m để hàm số:
a) Nghịch biến với mọi x > 0
b) Đồng biến với mọi x >0
c) Đạt giá trị lớn nhất là 0
d) Đạt giá trị nhỏ nhất là 0
Câu 2: Cho hàm số y = \(\left(\sqrt{3k+4}-3\right)x^2\) với k \(\ge\dfrac{-4}{3}\); k \(\ne\dfrac{5}{3}\)
Tính các giá trị của tham số K để hàm số:
a) Nghịch biến với mọi x >0
b) Đồng biến với mọi x >0
Câu 1:
a) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(3m+5< 0\)
\(\Leftrightarrow3m< -5\)
hay \(m< -\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(m< -\dfrac{5}{3}\)
b) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì
3m+5>0
\(\Leftrightarrow3m>-5\)
hay \(m>-\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì \(m>-\dfrac{5}{3}\)
2.
Để hàm nghịch biến với x>0 \(\Leftrightarrow\sqrt{3k+4}-3< 0\)
\(\Leftrightarrow\sqrt{3k+4}< 3\Leftrightarrow3k+4< 9\)
\(\Rightarrow-\dfrac{4}{3}\le k< \dfrac{5}{3}\)
Để hàm đồng biến khi x>0
\(\Leftrightarrow\sqrt{3k+4}-3>0\Leftrightarrow\sqrt{3k+4}>3\)
\(\Leftrightarrow3k+4>9\Rightarrow k>\dfrac{5}{3}\)
Câu 4: Tìm các giá trị thực của tham số m để hàm số\(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đạt tại x= 3
Cho hàm số \(y=x^4-2mx^2+m\) và điểm A có hoành độ bằng 1 thuộc đồ thị hàm số. Tìm giá trị tham số m, biết rằng khoảng cách từ điểm \(B\left(\dfrac{3}{4};1\right)\) đến tiếp tuyến tại A đạt giá trị lớn nhất:
A. \(m=-1\)
B. \(m=0\)
C. \(m=1\)
D. \(m=2\)
\(y'=4x^3-4mx\Rightarrow y'\left(1\right)=4-4m\)
\(A\left(1;1-m\right)\)
Phương trình tiếp tuyến d tại A có dạng:
\(y=\left(4-4m\right)\left(x-1\right)+1-m\)
\(\Leftrightarrow\left(4-4m\right)x-y+3m-3=0\)
\(d\left(B;d\right)=\dfrac{\left|\dfrac{3}{4}\left(4-4m\right)-1+3m-3\right|}{\sqrt{\left(4-4m\right)^2+1}}=\dfrac{1}{\sqrt{\left(4-4m\right)^2+1}}\le1\)
Dấu "=" xảy ra khi và chỉ khi \(4-4m=0\Rightarrow m=1\)
y′=4x3−4mx⇒y′(1)=4−4my′=4x3−4mx⇒y′(1)=4−4m
A(1;1−m)A(1;1−m)
Phương trình tiếp tuyến d tại A có dạng:
y=(4−4m)(x−1)+1−my=(4−4m)(x−1)+1−m
⇔(4−4m)x−y+3m−3=0⇔(4−4m)x−y+3m−3=0
Câu 1: Tìm giá trị thực của tham số m để hàm số
y= \(\dfrac{1}{3}x^3-mx^{2^{ }}+\left(m^2-4\right)x+3\) tại x=3
Câu 2:Tìm m để hàm số \(y=x^3-2mx^2+mx+1\) đạt cực tiểu tại x=1
Cho hàm số f(x) = x - 1 2 a x 2 + 4 a x - a + b - 2 , với a,b ∈ ℝ . Biết trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1. Hỏi trên đoạn - 2 ; - 5 4 , hàm số đạt giá trị nhỏ nhất tại giá trị nào của x?
A. x = - 5 4
B. x = - 4 3
C. x = - 3 2
D. x = -2
Chọn C
Tập xác định của hàm số là ℝ .
Ta có: ![]()
Vì trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1 nên hàm số đạt cực trị tại x = -1( cũng là điểm cực đại của hàm số) và a > 0.
![]()
![]()
![]()
Khi đó f'(x) = 0 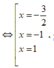 ( đều là các nghiệm đơn)
( đều là các nghiệm đơn)
Hàm số đạt cực đại tại x = -1 nên có bảng biến thiên:
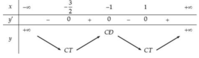
=> x = - 3 2 là điểm cực tiểu duy nhất thuộc - 2 ; - 5 4
Vậy hàm số đạt giá trị nhỏ nhất tại x = - 3 2 trên đoạn - 2 ; - 5 4
Cho hàm số y = (4m + 2) x2 với m ≠ -\(\dfrac{1}{2}\). Tìm các giá trị của tham số m để hàm số :
a) Nghịch biến với mọi x < 0
b) Đạt giá trị lớn nhất là 0
a,nghịch biến x<0
`<=>4m+2<0`
`<=>4m< -2`
`<=>m< -1/2`
`b,(4m+2)x^2<=0`
Mà `x^2>=0`
`<=>4m+2<0`
`<=>4m<-2`
`<=>m<-1/2`
a) Để hàm số nghịch biến với mọi x<0 thì 4m+2>0
\(\Leftrightarrow4m>-2\)
hay \(m>-\dfrac{1}{2}\)
Vậy: Để hàm số nghịch biến với mọi x<0 thì \(m>-\dfrac{1}{2}\)
b) Để hàm số đạt giá trị lớn nhất là 0 thì 4m+2<0
hay \(m< -\dfrac{1}{2}\)
Câu 6: Tìm các giá trị thực của tham số m để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đạt tại x=3
Tìm giá trị lớn nhất của hàm số: y=\(\dfrac{x}{\left(x+1\right)^2}\), x>0.
\(\dfrac{1}{y}=\dfrac{x^2+2x+1}{x}=x+\dfrac{1}{x}+2\ge2\sqrt{x.\dfrac{1}{x}}+2=4\)
\(\Rightarrow y\le\dfrac{1}{4}\)
\(y_{max}=4\) khi \(x=1\)