Các câu hỏi tương tự
Cho hàm số y = \(|2x-x^2-\sqrt{\left(x+1\right)\left(3-x\right)}+b|\)Để giá trị lớn nhất của hàm số đạt giá trị nhỏ nhất thì giá trị của b thuộc khoảng nào
cho hàm số y = \(|2x-x^2-\sqrt{\left(x+1\right)\left(3-x\right)}+b|\) Để giá trị lớn nhất đạt giá trị nhỏ nhất thì giá trnàoị của b thuộc khoảng
có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số
\(y=\dfrac{x-1}{\sqrt{mx^2-8x+2}}\) có đúng bốn đường tiệm cận (anh/chị giúp em câu này với.Em cảm ơn trước ạ )
Gọi M, m lần lượt là giá trị lớn nhất , giá trị nhỏ nhất của hàm số y = x(2017 +\(\sqrt{2019-x^2}\)) trên tập xác định của nó . Tính M-m
Xét tính đơn điệu của các hàm số sau:
\(y = {x^2 -1 \over x^2 +1} trong ( 0; + vô cùng)\)
\(y = {x^4-4x^3 \over x-1} \)
\(y = { \sqrt{x} -x}\)
\(y={x^2\over\sqrt {x^2-1}}\)
Tìm tất cả giá trị của m để hàm số y=\(\sqrt{x^2+2mx+m^2+1}\) đồng biến trên khoảng (1;+∞)
Giá trị lớn nhất của hàm số
y
x
+
4
+
4
-
x
-
4
x
+
4
4
-
x
+
5
bằng A.
m
a
x...
Đọc tiếp
Giá trị lớn nhất của hàm số y = x + 4 + 4 - x - 4 x + 4 4 - x + 5 bằng
A. m a x [ - 4 ; 4 ] y = 10
B. m a x [ - 4 ; 4 ] y = 5 - 2 2
C. m a x [ - 4 ; 4 ] y = - 7
D. m a x [ - 4 ; 4 ] y = 5 + 2 2
Cho hàm số f(x) có đạo hàm là f(x). Đồ thị của hàm số y f(x) được cho như hình vẽ dưới đây: Biết rằng f(-1) + f(0) f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y f(x) trên đoạn [-1;2] lần lượt là: A. f(1);f(2) B. f(2);f(0) C. f(0);f(2) D. f(1);f(-1)
Đọc tiếp
Cho hàm số f(x) có đạo hàm là f'(x). Đồ thị của hàm số y = f'(x) được cho như hình vẽ dưới đây:
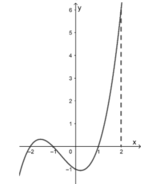
Biết rằng f(-1) + f(0) < f(1) + f(2). Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = f(x) trên đoạn [-1;2] lần lượt là:
A. f(1);f(2)
B. f(2);f(0)
C. f(0);f(2)
D. f(1);f(-1)
Câu 1: Tìm giá trị thực của tham số m để hàm số
y= \(\dfrac{1}{3}x^3-mx^{2^{ }}+\left(m^2-4\right)x+3\) tại x=3
Câu 2:Tìm m để hàm số \(y=x^3-2mx^2+mx+1\) đạt cực tiểu tại x=1








