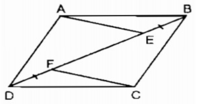
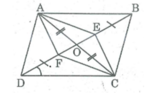
Gọi O là giao điểm của AC và BD, ta có:

OB = OE + EB và OD = OF+ FD (1)

Lại có: EB = FD (giả thiết) (2)

OB = OD ( tính chất hình bình hành). (3)

Từ (1), (2),(3) suy ra: OE = OF

Suy ra tứ giác AECF là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường)

⇒ AE // CF.

Vì ABCD là hình bình hành

=> + AB = DC

       AB // DC  => góc ABE = góc FCD  ( sole trong )

+     AD= BC

     AD // BC

+) Xét \(\Delta AEB\)và \(\Delta CFD\)có :

\(AB=CD\left(cmt\right)\)

\(\widehat{AEB}=\widehat{CFD}=90^o\)(gt )

\(\widehat{ABE}=\widehat{FCD}\)(cmt)

Do đó : tam giác vuông AEB = tam giác vuông CFD ( cạnh huyền - góc nhọn )

\(\Rightarrow AE=FC\)( cặp cạnh tương ứng )               (1)

+)  vÌ \(\hept{\begin{cases}AE\perp DB\\FC\perp DB\end{cases}}\)

=> AE // FC  (2)

Từ (1) và (2)

=>  AECF là hình bình hành ( đpcm )

Hình hơi xấu nha ^^

a: Xét ΔADE vuông tại E và ΔCBF vuông tại F có 

AD=CB

\(\widehat{ADE}=\widehat{CBF}\)

Do đó: ΔADE=ΔCBF

Suy ra: AE=CF

b: Xét tứ giác AECF có 

AE//CF

AE=CF

Do đó: AECF là hình bình hành

Ta có: AE+EB=AB

CF+FD=CD

mà AB=CD

và AE=CF

nên EB=FD

Ta có: AH+HD=AD

CG+BG=CB

mà AD=CB

và HD=BG

nên AH=CG

Xét ΔAHE và ΔCGF có 

AH=CG

\(\widehat{A}=\widehat{C}\)

AE=CF

Do đó: ΔAHE=ΔCGF

Suy ra: HE=GF

Xét ΔEBG và ΔFDH có 

EB=FD

\(\widehat{B}=\widehat{D}\)

BG=DH

Do đó: ΔEBG=ΔFDH

Suy ra: EG=FH

Xét tứ giác EHFG có

EG=FH

EH=FG

Do đó: EHFG là hình bình hành

*AF cắt DC tại G.

-△APE có: AE//CG (ABCD là hình bình hành) \(\Rightarrow\dfrac{AP}{PG}=\dfrac{AE}{CG}\) (hệ quả định lý Ta-let) mà \(AE=CF\left(gt\right)\) \(\Rightarrow\dfrac{AP}{PG}=\dfrac{CF}{CG}\)

-△ADG có: CF//AD (ABCD là hình bình hành) \(\Rightarrow\dfrac{CF}{AD}=\dfrac{CG}{DG}\Rightarrow\dfrac{AD}{DG}=\dfrac{CF}{CG}=\dfrac{AP}{PG}\)

*AH//DP (H thuộc DC)

△AHG có: AH//DP (gt) \(\Rightarrow\dfrac{AP}{PG}=\dfrac{DH}{DG}=\dfrac{AD}{DG}\Rightarrow DH=AD\)

\(\Rightarrow\)△ADH cân tại D. \(\Rightarrow\widehat{HAD}=\widehat{ADH}=\widehat{ADP}=\widehat{CDP}\)

\(\Rightarrow\)DP là tia phân giác của góc ADC

Làm giúp mình với ạ mình cần tối nay ạ 

a: Xét ΔAEB và ΔCFD có 

AB=CD

\(\widehat{ABE}=\widehat{CDF}\)

BE=DF

Do đó: ΔAEB=ΔCFD

Suy ra: \(\widehat{AEB}=\widehat{CFD}\)

\(\Leftrightarrow\widehat{AEF}=\widehat{EFC}\)

mà hai góc này là hai góc ở vị trí đồng vị

nên AE//CF

a: Ta có: AE+EB=AB

DF+FC=DC

mà AE=FC

và AB=DC

nên EB=DF

Xét tứ giác EBFD có 

EB//DF

EB=DF

Do đó: EBFD là hình bình hành

Suy ra: DE=BF

b: Xét tứ giác AECF có 

AE//CF

AE=CF

Do đó: AECF là hình bình hành

K ở đâu ra em?

a: Xét tứ giác AECF có 

AE//CF

AE=CF

Do đó: AECF là hình bình hành

b: Ta có: AE+EB=AB

FC+FD=CD

mà AB=CD

và AE=FC

nên EB=FD

Xét tứ giác EBFD có 

EB//FD

EB=FD

DO đó: EBFD là hình bình hành

Suy ra: DE=BF