 trình bày rõ ràng chi tiết nhất ko làm tắt ạ e cảm ơn và kèm lói giải thích cụ thể
trình bày rõ ràng chi tiết nhất ko làm tắt ạ e cảm ơn và kèm lói giải thích cụ thể
Bài 7: Hình bình hành
a: Xét ΔMQP có
H,I lần lượt là trung điểm của MQ,MP
=>HI là đường trung bình của ΔMQP
=>HI//QP và HI=QP/2
Xét ΔPMN có
I,K lần lượt là trung điểm của PM,PN
=>IK là đường trung bình của ΔPMN
=>IK//MN và \(IK=\dfrac{MN}{2}\)
b: H,I,K thẳng hàng
mà HI//PQ và IK//MN
nên HI//MN
Ta có: HI//MN
HI//PQ
Do đó: MN//PQ
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH kẻ HM vuông góc với AB tại M và HN vuông góc tAC tại N
c, lấy điểm D đối xứng với h điểm H qua điểm M Chứng minh ba điểm D a k thẳng hàng và chứng minh bc² = bc bình phương + ck bình phương+ 2bh x HC
c: Sửa đề: D đối xứng với H qua M
Xét ΔAHK có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔAHK cân tại A
Ta có: ΔAHK cân tại A
mà AC là đường cao
nên AC là phân giác của góc HAK
=>\(\widehat{HAK}=2\cdot\widehat{HAC}\)
Xét ΔAHD có
AM là đường cao
AM là đường trung tuyến
Do đó: ΔAHD cân tại A
Ta có: ΔAHD cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAD
=>\(\widehat{HAD}=2\cdot\widehat{HAB}\)
Ta có: \(\widehat{HAK}+\widehat{HAD}=\widehat{DAK}\)
=>\(\widehat{DAK}=2\cdot\widehat{HAB}+2\cdot\widehat{HAC}\)
=>\(\widehat{DAK}=2\left(\widehat{HAC}+\widehat{HAB}\right)=2\cdot\widehat{BAC}=2\cdot90^0=180^0\)
=>D,A,K thẳng hàng
Sửa đề: \(BD^2+CK^2+2\cdot BH\cdot HC\)
Xét ΔBHD có
BM là đường cao
BM là đường trung tuyến
Do đó: ΔBHD cân tại B
=>BH=BD
Xét ΔCKH có
CN là đường cao
CN là đường trung tuyến
Do đó: ΔCKH cân tại C
=>CK=CH
\(BD^2+CK^2+2\cdot BH\cdot HC\)
\(=BH^2+HC^2+2\cdot BH\cdot HC\)
\(=\left(BH+HC\right)^2=BC^2\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N
a, Chứng minh tứ giác amhn là hình chữ nhật
b, lấy điểm K sao cho n là trung điểm của HK Chứng minh tứ giác amnk là hình bình hành
a: Xét tứ giác AMHN có
\(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
=>AMHN là hình chữ nhật
b: Ta có: AMHN là hình chữ nhật
=>AM//HN và AM=HN
Ta có: AM//HN
N\(\in\)HK
Do đó: AM//KN
Ta có: AM=HN
HN=KN
Do đó: AM=KN
Xét tứ giác AMNK có
AM//NK
AM=NK
Do đó: AMNK là hình bình hành
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A đường cao AH kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N
a, Chứng minh tứ giác amhn là hình chữ nhật
b, lấy điểm K sao cho n là trung điểm của HK Chứng minh tứ giác amnk là hình bình hành
Tam giác ABC cân tại A ,trung tuyến BM,vẽ D là điểm đối xứng với B qua C,chứng minh góc ABM= góc CAD
Cần gấp lm ơn
cho hình bình hành ABCD. Gọi E là trung điểm của AB, F là trung điểm của CD: a) chứng minh tứ giác AECF là hình bình hành b) DE cắt AC tại I, BF cắt AC tại K. Chứng minh rằng AI=IK=KC
Xem chi tiết
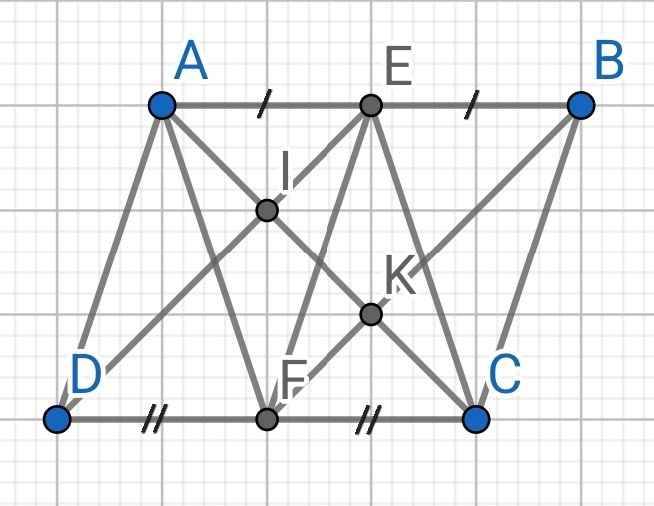 a) Do ABCD là hình bình hành (gt)
a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC
Đúng 2
Bình luận (0)
22:
Ta có: \(EA=ED=\dfrac{AD}{2}\)
\(CF=BF=\dfrac{CB}{2}\)
mà AD=CB
nên EA=ED=CF=BF
Xét tứ giác DEBF có
DE//BF
DE=BF
Do đó: DEBF là hình bình hành
=>BE//DF và BE=DF
24:
a: AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)(hai góc so le trong, AH//CK)
Do đó: ΔAHD=ΔCKB
=>AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
b: AHCK là hình bình hành
=>AC cắt HK tại trung điểm của mỗi đường
mà O là trung điểm của HK
nên O là trung điểm của AC
=>A,O,C thẳng hàng
c: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của BD
O là trung điểm của BD
=>B đối xứng D qua O
O là trung điểm của AC
=>A đối xứng C qua O
O là trung điểm của HK
=>H đối xứng K qua O
Đúng 0
Bình luận (0)
cho hbh ancd có k là trung điểm của ab i là trung điểm của cd.kẻ bd sao cho m là trung điểm của ai,n là trung điểm của kc.CM a,∆adm =∆cbn b,góc man = góc nca và im // nc c,AC,BD,IK thẳng hàng
a: \(AK=KB=\dfrac{AB}{2}\)
\(DI=IC=\dfrac{DC}{2}\)
mà AB=DC
nên AK=KB=DI=IC
Xét tứ giác AKCI có
AK//CI
AK=CI
Do đó: AKCI là hình bình hành
=>AI=CK và AI//CK
M là trung điểm của AI
=>\(AM=MI=\dfrac{AI}{2}\)
N là trung điểm của CK
=>\(NK=NC=\dfrac{CK}{2}\)
mà AI=CK
nên AM=NI=NK=NC
AKCI là hình bình hành
=>\(\widehat{KAI}=\widehat{KCI}\)
\(\widehat{KAI}+\widehat{DAI}=\widehat{DAB}\)
\(\widehat{KCI}+\widehat{KCB}=\widehat{BCD}\)
mà \(\widehat{KAI}=\widehat{KCI};\widehat{DAB}=\widehat{BCD}\)
nên \(\widehat{DAI}=\widehat{KCB}\)
Xét ΔADM và ΔCBN có
AD=CB
\(\widehat{DAM}=\widehat{BCN}\)
AM=CN
Do đó: ΔADM=ΔCBN
b: Sửa đề: góc MAN=góc NCM
Xét tứ giác MANC có
MA//NC
MA=NC
Do đó: MANC là hình bình hành
=>\(\widehat{MAN}=\widehat{MCN}\)
AI//CK
\(M\in AI\)
\(N\in CK\)
Do đó: IM//NC
c: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường(1)
AKCI là hình bình hành
=>AC cắt KI tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra AC,BD,KI đồng quy
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có BC = 2AB và góc A = 60 độ . goị EF theo thứ tự là trung điểm BC,AD . lấy điểm I sao cho B là trung điểm của AI
Đề bài yêu cầu gì vậy bạn?
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và góc OAD = OCB. Chứng minh tứ giác ABCD là hình bình hành.
Lưu ý: Giải cách khác ngoài cách chứng minh 2 đường chéo
Xét ΔOAD và ΔOCB có
\(\widehat{OAD}=\widehat{OCB}\)
OA=OC
\(\widehat{AOD}=\widehat{COB}\)
Do đó: ΔOAD=ΔOCB
=>AD=BC
\(\widehat{OAD}=\widehat{OCB}\)
mà hai góc này ở vị trí so le trong
nên AD//BC
Xét tứ giác ABCD có
AD//BC
AD=BC
Do đó: ABCD là hình bình hành
Đúng 2
Bình luận (0)















