Ôn tập chương I : Tứ giác
Nội dung lý thuyết
TÓM TẮT KIẾN THỨC CẦN NHỚ
1. Tứ giác
- Tứ giác \(ABCD\) là hình gồm bốn đoạn thẳng \(AB,BC,CD,DA\), trong đó không có hai đoạn thẳng nào nằm trên một đường thẳng.
- Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.
- Tổng các góc của tứ giác bằng \(360^0\).
2. Hình thang. Hình thang cân
- Hình thang là tứ giác có hai cạnh đối song song.
- Hình thang vuông là hình thang có một góc vuông.
- Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
- Trong hình thang cân, hai cạnh bên bằng nhau, hai đường chéo bằng nhau.
- Dấu hiệu nhận biết hình thang cân:
+) Hình thang có hai góc kề một đáy bằng nhau là hình thang cân. +) Hình thang có hai đường chéo bằng nhau là hình thang cân. |
3. Đường trung bình của tam giác, của hình thang
- Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Đường trung bình của tam giác song song với cạnh thứ ba và bằng một nửa cạnh ấy.
- Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên hình thang.
- Đường trung bình của hình thang song song với hai đáy và bằng nửa tổng hai đáy.
4. Hình bình hành
- Hình bình hành là tứ giác có các cạnh đối song song.
- Hình bình hành là hình thang đặc biệt.
- Tính chất: Các cạnh đối bằng nhau; Các góc đối bằng nhau; Hai đường chéo cắt nhau tại trung điểm mỗi đường.
- Dấu hiệu nhận biết:
+) Tứ giác có các cạnh đối song song là hình bình hành. +) Tứ giác có các cạnh đối bằng nhau là hình bình hành. +) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành. +) Tứ giác có các góc đối bằng nhau là hình bình hành. +) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành. |
5. Hình chữ nhật
- Hình chữ nhật là tứ giác có bốn góc vuông.
- Hình chữ nhật cũng là một hình thang cân, cũng là một hình bình hành.
- Tính chất: Các cạnh đối song song và bằng nhau; Hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
- Dấu hiệu nhận biết:
+) Tứ giác có ba góc vuông là hình chữ nhật. +) Hình bình hành có một góc vuông là hình chữ nhật. +) Hình thang cân có một góc vuông là hình chữ nhật. +) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật. |
- Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
- Một tam giác có đường trung tuyến ứng với một cạnh bằng một nửa cạnh ấy thì tam giác đó là tam giác vuông.
6. Hình thoi
- Hình thoi là tứ giác có bốn cạnh bằng nhau.
- Hình thoi cũng là một hình bình hành.
- Tính chất: Các góc đối bằng nhau; Hai đường chéo vuông góc với nhau tại trung điểm mỗi đường và là đường phân giác của các góc của hình thoi.
- Dấu hiệu nhận biết:
+) Tứ giác có bốn cạnh bằng nhau là hình thoi. +) Hình bình hành có hai cạnh kề bằng nhau là hình thoi. +) Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi. +) Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi. |
7. Hình vuông
- Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
- Hình vuông vừa là hình chữ nhật, vừa là hình thoi.
- Tính chất: Các cạnh bằng nhau; Các góc bằng nhau; Hai đường chéo bằng nhau và vuông góc với nhau tại trung điểm mỗi đường, cũng là phân giác các góc của hình vuông.
- Dấu hiệu nhận biết:
+) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông. +) Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông. +) Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông. +) Hình thoi có một góc vuông là hình vuông. +) Hình thoi có hai đường chéo bằng nhau là hình vuông. |
8. Đối xứng trục. Đối xứng tâm
- Hai hình đối xứng nhau qua một đường thẳng nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng đó và ngược lại.
- Đường thẳng \(d\) là trục đối xứng của hình H nếu điểm đối xứng của mỗi điểm thuộc hình H qua đường thẳng \(d\) cũng thuộc hình H.
- Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.
- Hai hình đối xứng nhau qua điểm \(O\) nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm \(O\) và ngược lại.
- Điểm \(O\) là tâm đối xứng của hình H nếu điểm đối xứng của mỗi điểm thuộc hình H qua điểm \(O\) cũng thuộc hình H.
- Nếu hai đoạn thẳng (góc, tam giác) đối xứng với nhau qua một điểm thì chúng bằng nhau.
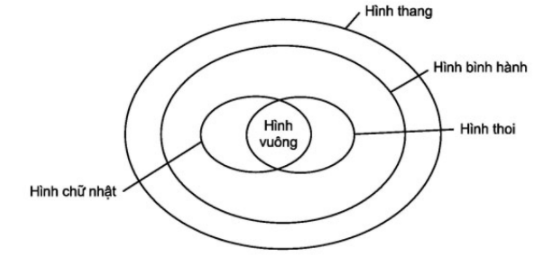
9. Mối quan hệ giữa các tứ giác đặc biệt
@626449@