Bài 4: Đường trung bình của tam giác, hình thang

1. Đường trung bình của tam giác

Xét bài toán: Cho tam giác \(ABC\), \(D\) là trung điểm \(AB\). Qua \(D\) vẽ đường thẳng song song với \(BC\), cắt \(AC\) tại \(E\). Ta sẽ chứng minh được: \(E\) là trung điểm \(AC\).

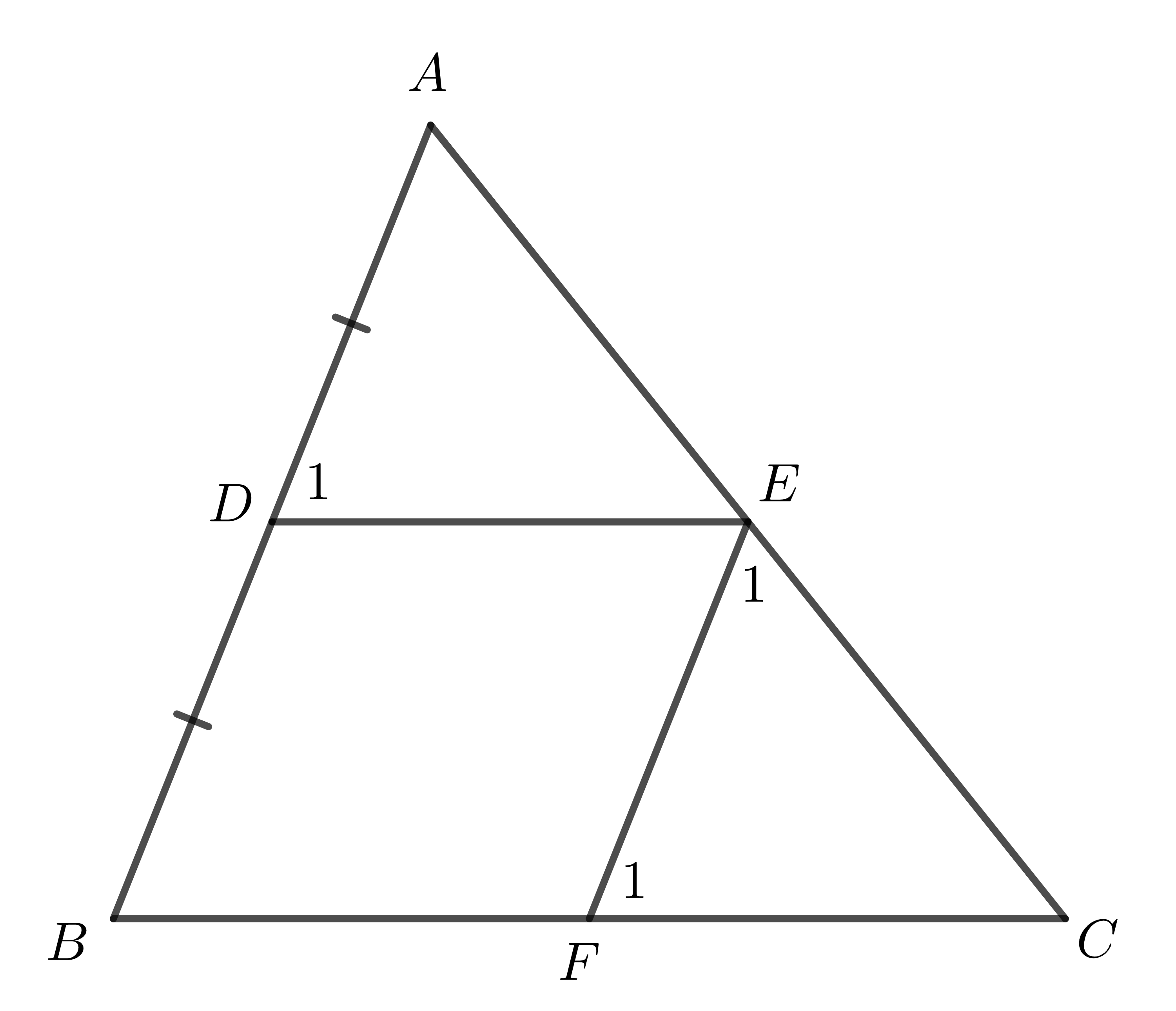
Thật vậy:

Qua \(E\) kẻ đường thẳng song song với \(AB\), cắt \(BC\) tại \(F\). Do \(DE\) // \(BF\) nên \(BDEF\) là hình thang.

Lại có \(BD\) // \(EF\) \(\Rightarrow BD=EF=AD\).

Xét \(\Delta ADE\) và \(\Delta EFC\) có:

• \(\widehat{A}=\widehat{E_1}\) (hai góc đồng vị);
• \(AD=EF\) (chứng minh trên);
• \(\widehat{D_1}=\widehat{F_1}\) (cùng bằng \(\widehat{B}\))

\(\Rightarrow\Delta ADE=\Delta EFC\) (góc - cạnh - góc) \(\Rightarrow AE=EC\) (hai góc tương ứng).

Vậy \(E\) là trung điểm \(AC\).

Nội dung bài toán trên được phát biểu thành định lí:

Định lí 1: Đường thẳng đi qua trung điểm của một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.

Trong hình vẽ phía trên ta có \(D\), \(E\) lần lượt là trung điểm \(AB,AC\). Ta gọi \(DE\) là một đường trung bình của tam giác \(ABC\).

Định nghĩa: Đường trung bình của tam giác là đường thẳng nối trung điểm hai cạnh của tam giác.

Ta chứng minh được tính chất sau về đường trung bình của một tam giác:

Định lí 2: Đường trung bình của một tam giác thì song song với cạnh thứ ba và song song với cạnh ấy.

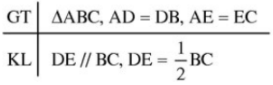
Lấy điểm \(F\) sao cho \(E\) là trung điểm \(DF\) (hình vẽ).

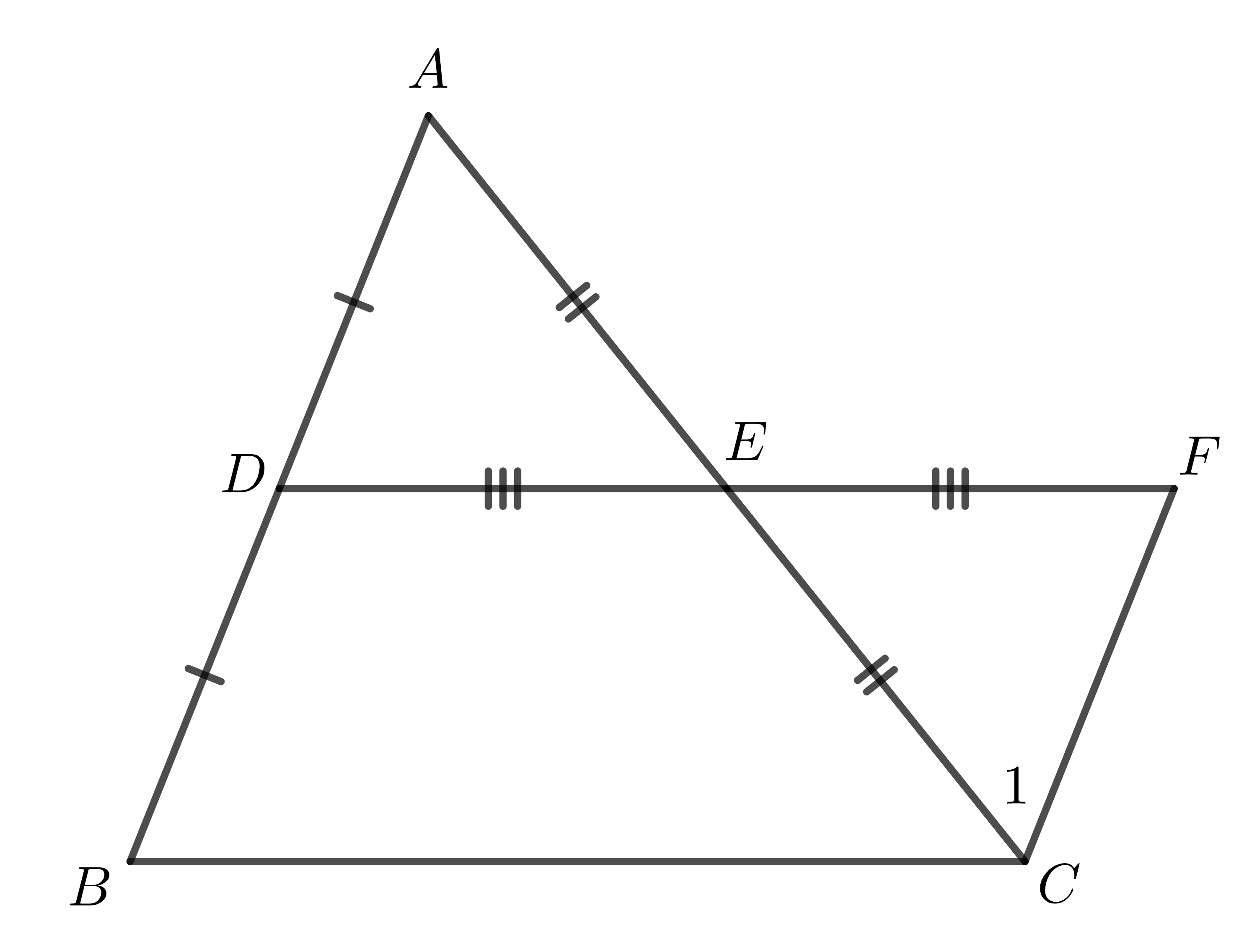
Ta dễ dàng chứng minh được \(\Delta ADE=\Delta CFE\) (cạnh - góc - cạnh)

\(\Rightarrow AD=CF\) và \(\widehat{A}=\widehat{C_1}\).

Do \(AD=CF;AD=BD\Rightarrow BD=CF\).

Do \(\widehat{A}=\widehat{C_1}\) mà hai góc so le trong \(\Rightarrow AB\)//\(CF\) hay \(BD\)//\(CF\)

\(\Rightarrow BDFC\) là hình thang, mà \(BD=CF\) \(\Rightarrow DF=BC\) và \(DF\)//\(BC\).

Do đó ta suy ra \(DE\)//\(BC\) và \(DE=\dfrac{1}{2}BC\) (Điều phải chứng minh).

Ví dụ: Cho tam giác \(ABC\) có \(BC=10cm\). Gọi \(D,E\) lần lượt là trung điểm \(AB,AC\). Khi đó ta có \(DE\) là đường trung bình của tam giác \(ABC\) \(\Rightarrow DE=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right).\)

Nhận xét: Mỗi tam giác có 3 đường trung bình (mỗi đường song song với một cạnh của tam giác).

2. Đường trung bình của hình thang

Xét bài toán: Cho hình thang \(ABCD\) (\(AB\)//\(CD\)). Qua \(E\) là trung điểm của \(AD\), kẻ đường thẳng song song với hai đáy, đường thẳng này cắt \(BC\) tại \(F\). Ta chứng mình được: \(F\) là trung điểm \(BC\).

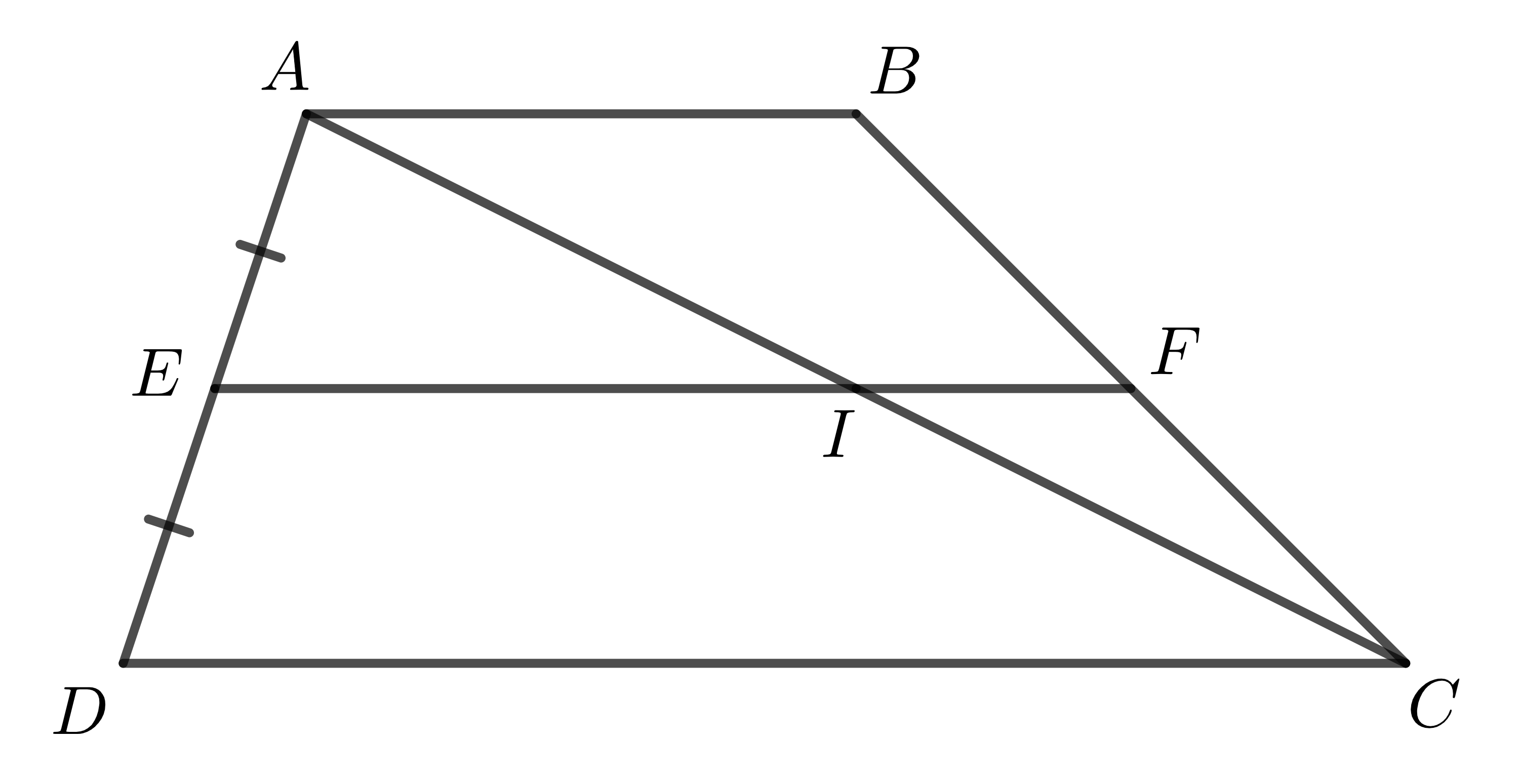
Gọi \(I\) là giao điểm \(AC,EF\). 

Tam giác \(ACD\) có \(E\) là trung điểm \(AD\), \(EI\)//\(CD\) nên \(I\) là trung điểm \(AC\) (theo định lí 1).

Tam giác \(ACB\) có \(I\) là trung điểm \(AC\), \(IF\)//\(AB\) \(\Rightarrow F\) là trung điểm \(BC\) (Điều phải chứng minh).

Nội dung bài toán trên cho ta một định lí:

Định lí 3: Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên còn lại.

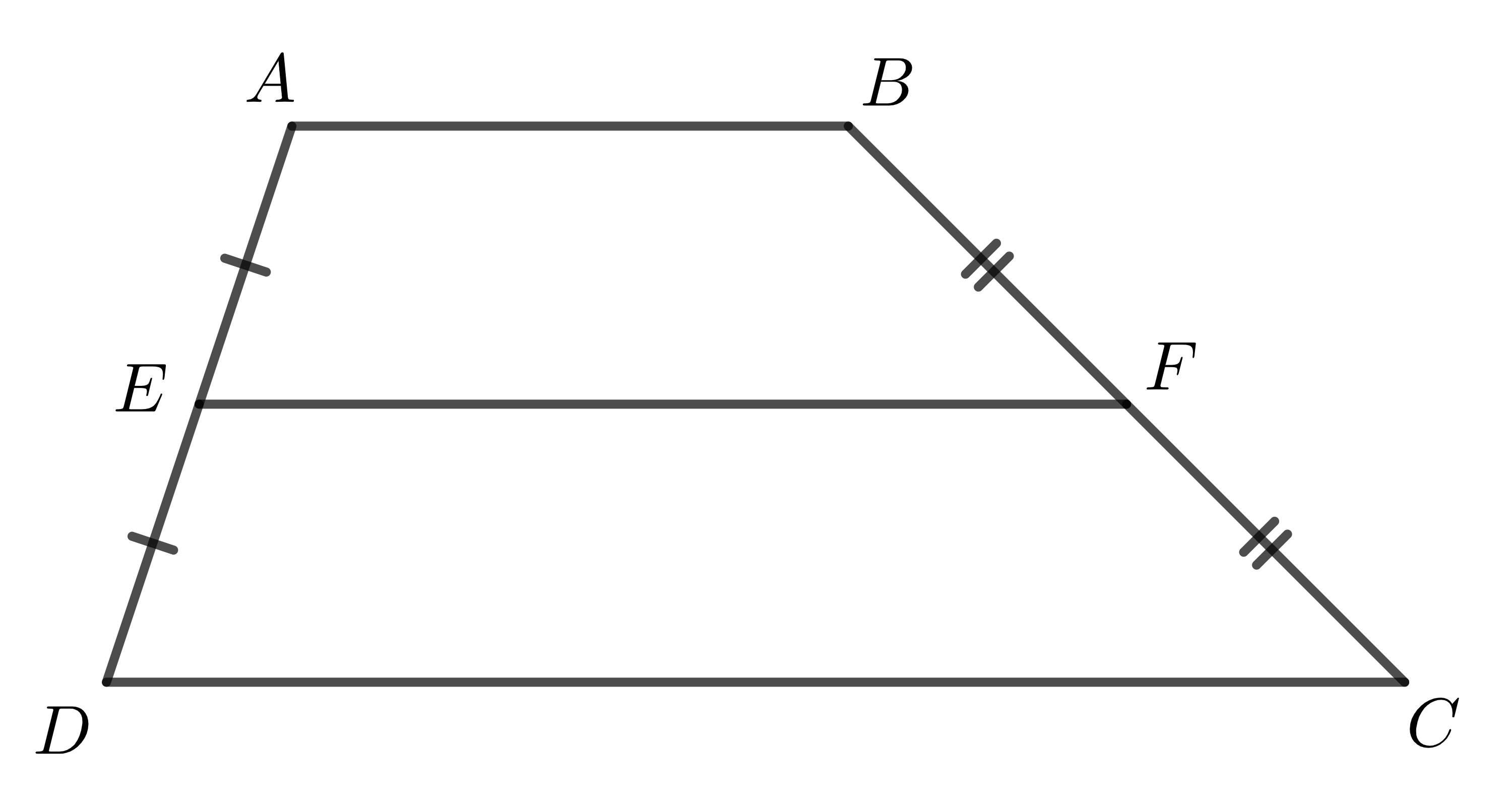
Trong hình trên, hình thang \(ABCD\) có \(E,F\) lần lượt là trung điểm hai cạnh bên \(AD,BC\). Ta gọi \(EF\) là đường trung bình của hình thang \(ABCD\). 

Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điềm hai cạnh bên của hình thang.

Ta có định lí: 

Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

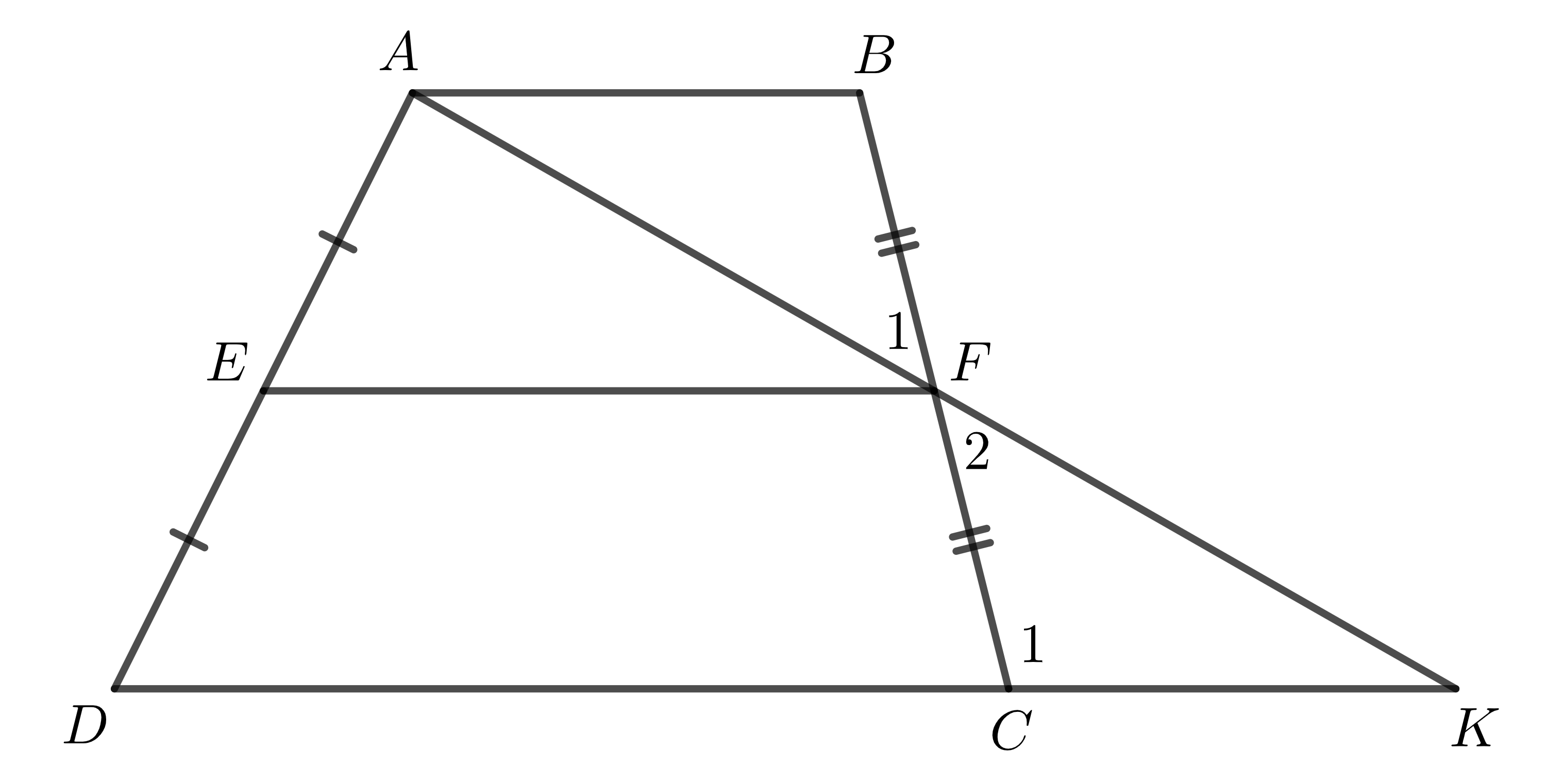
Gọi \(AF\cap CD\equiv K\). Xét \(\Delta FAB\) và \(\Delta FKC\) có:

• \(\widehat{F_1}=\widehat{F_2}\) (hai góc đối đỉnh);
• \(BF=CF\) (giả thiết);
• \(\widehat{B}=\widehat{C_1}\) (hai góc so le trong)

\(\Rightarrow\Delta FAB=\Delta FKC\) (góc - cạnh - góc) \(\Rightarrow\left\{{}\begin{matrix}AB=CK\\AF=KF\end{matrix}\right.\).

Ta có \(E,F\) lần lượt là trung điểm \(AD,AK\) \(\Rightarrow EF\) là đường trung bình của tam giác \(ADK\)

\(\Rightarrow EF\)//\(DK\) (hay \(EF\)//\(AB\), \(EF\)//\(CD\)) và \(EF=\dfrac{1}{2}DK=\dfrac{1}{2}\left(CD+CK\right)=\dfrac{1}{2}\left(AB+CD\right).\)

Đây chính là điều cần chứng minh.

Ví dụ: Cho hình thang \(ABCD\) có \(AB\)//\(CD\). Gọi \(E,F\) lần lượt là trung điểm \(AD,BC\). Biết \(AB=6cm;EF=9cm\). Tính \(CD\)?

Ta có: \(E,F\) lần lượt là trung điểm \(AD,BC\) nên \(EF\) là đường trung bình của hình thang \(ABCD\)

\(\Rightarrow EF=\dfrac{AB+CD}{2}\Rightarrow CD=2.EF-AB=2.9-6=12\left(cm\right).\)

Nhận xét: Mỗi hình thang chỉ có duy nhất một đường trung bình.