Bài 3: Hình thang cân
Nội dung lý thuyết
1. Định nghĩa
Trong bài học trước ta đã biết: Hình thang là hình có hai cạnh đối song song. Sau đây, ta cùng tìm hiểu một hình thang rất đặc biệt: Hình thang cân.
Định nghĩa: Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
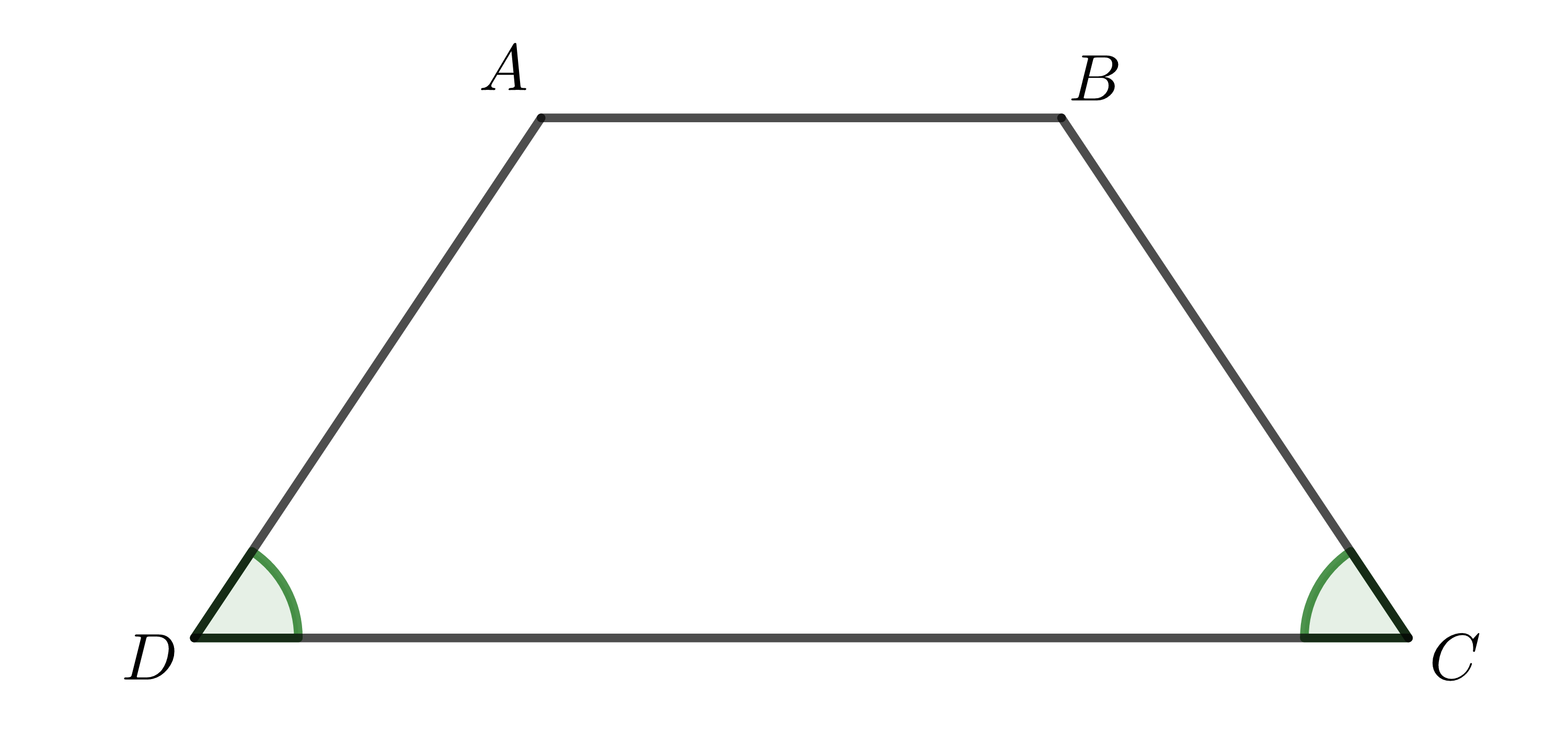
Trong hình vẽ trên, ta có hình thang \(ABCD\) với hai đáy \(AB\), \(CD\). Do \(\widehat{C}=\widehat{D}\), nên hình thang \(ABCD\) là một hình thang cân.
Như vậy:
Tứ giác \(ABCD\) là hình thang cân (đáy \(AB,CD\)) \(\Leftrightarrow \{ \begin{array}{1} AB\parallel CD\\ \hat{C}=\hat{D} \quad \text{hoặc}\quad \hat{A}=\hat{B} \end{array}\).
Chú ý: Nếu \(ABCD\) là hình thang cân (đáy \(AB,CD\)) thì ta có thể suy ra ngay \(\widehat{C}=\widehat{D}\) và \(\widehat{A}=\widehat{B}\).
Ta đã biết: \(\widehat{A}+\widehat{D}=\widehat{B}+\widehat{C}=180^0\) (tổng hai góc kề một cạnh bên). Khi \(\widehat{C}=\widehat{D}\), \(\widehat{A}=\widehat{B}\), ta dễ dàng suy ra: \(\widehat{A}+\widehat{C}=\widehat{B}+\widehat{D}=180^0\).
Nhận xét: Tổng hai góc đối nhau trong hình thang cân luôn bằng \(180^0\).
2. Tính chất
Hình thang cân có một số tính chất đặc trưng mà ta sẽ xét ngay sau đây:
Định lí 1: Trong hình thang cân, hai cạnh bên bằng nhau.

Ta sẽ chứng minh định lí trên bằng cách chia hai trường hợp:
Trường hợp 1: \(AD\) và \(BC\) không song song.
Giả sử \(AB< CD\). Gọi \(AD\cap BC\equiv O\).
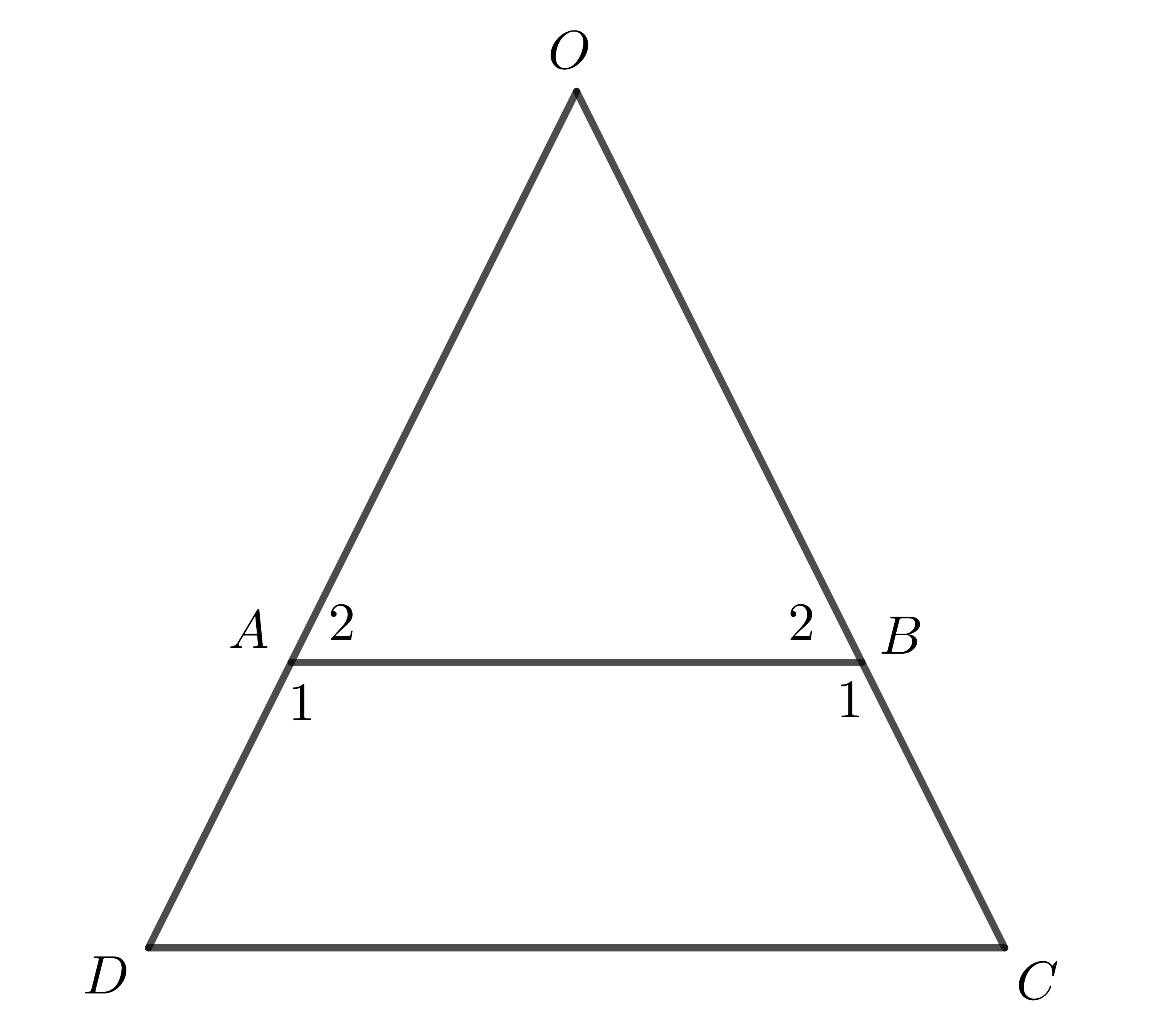
Do \(ABCD\) là hình thang cân nên \(\widehat{C}=\widehat{D};\widehat{A_1}=\widehat{B_1}.\)
Do \(\widehat{C}=\widehat{D}\) \(\Rightarrow\Delta OCD\) cân \(\Rightarrow OC=OD\).
Do \(\widehat{A_1}=\widehat{B_1}\Rightarrow\widehat{A_2}=\widehat{B_2}\Rightarrow\Delta OAB\) cân \(\Rightarrow OA=OB\).
\(\Rightarrow OD-OA=OC-OB\Rightarrow AD=BC\) (Điều phải chứng minh).
Trường hợp 2: \(AD\) song song \(BC\).

Ở bài trước ta đã biết: Hình thang có hai cạnh bên song song thì hai cạnh đáy bằng nhau, hai cạnh bên bằng nhau.
\(\Rightarrow AD=BC\) (Điều phải chứng minh).
Chú ý: Một hình thang có hai cạnh bên bằng nhau thì chưa chắc đã là hình thang cân. Ví dụ:
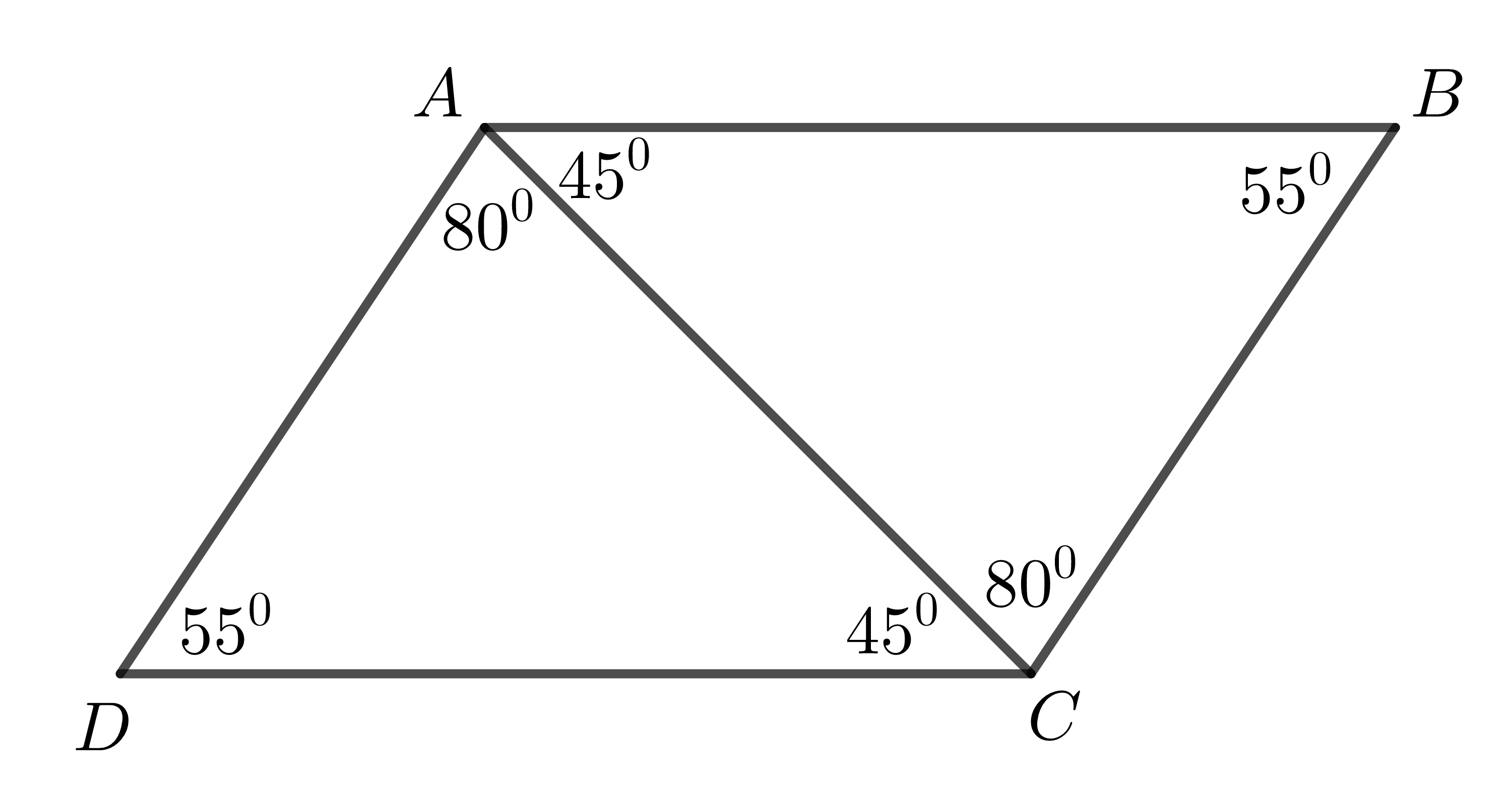
Hình thang \(ABCD\) trong hình trên có \(AD=BC\) nhưng không là hình thang cân do \(\widehat{A}\ne\widehat{B};\widehat{C}\ne\widehat{D}.\)
Định lí 2: Trong hình thang cân, hai đường chéo bằng nhau.
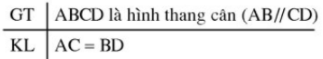
Chứng minh:
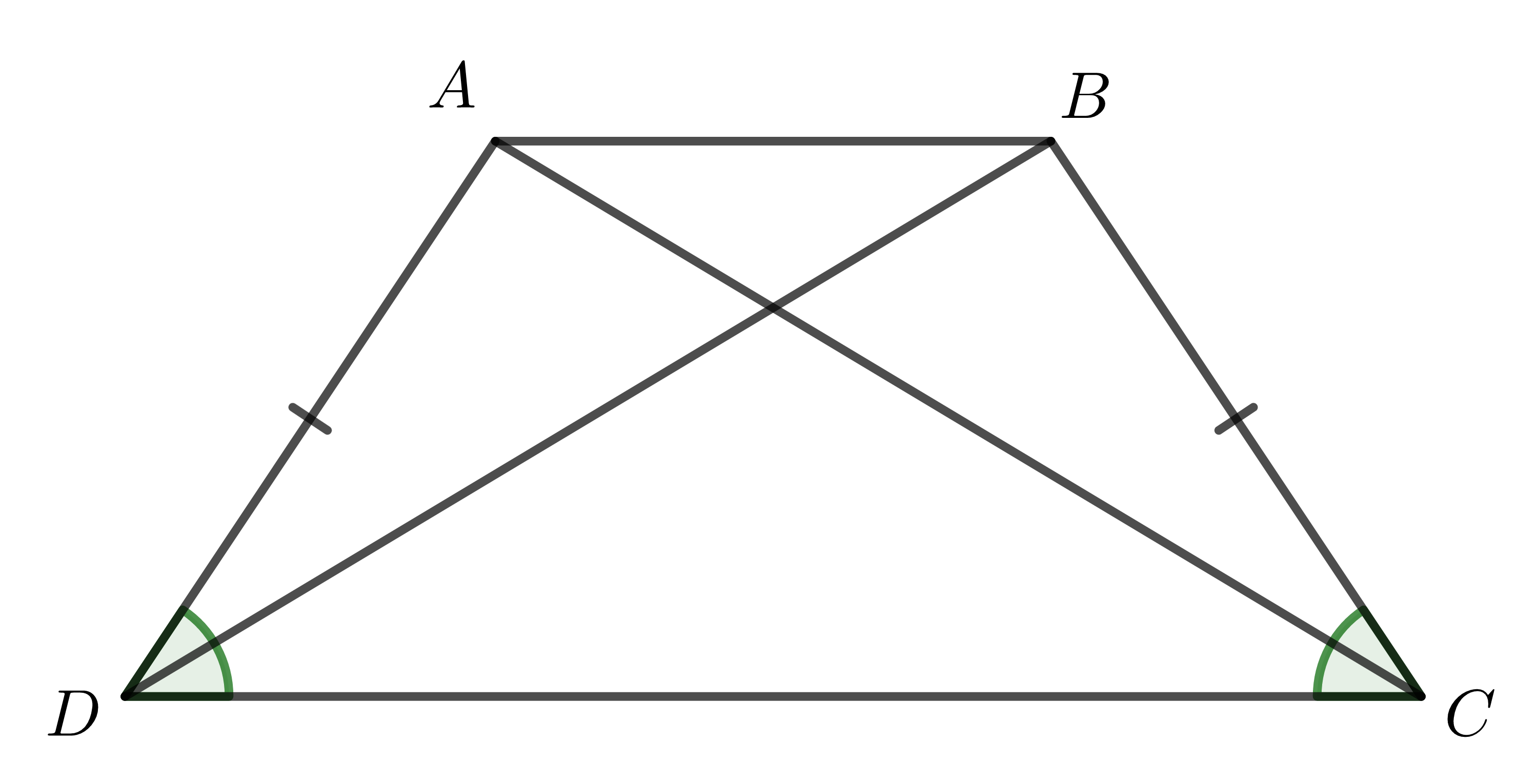
Xét tam giác \(ACD\) và tam giác \(BDC\) có:
- \(CD\) chung;
- \(\widehat{ADC}=\widehat{BCD}\) (do \(ABCD\) là hình thang cân);
- \(AD=BC\) (định lí 1)
\(\Rightarrow\Delta ACD=\Delta BDC\) (cạnh - góc - cạnh) \(\Rightarrow AC=BD\) (Điều phải chứng minh).
Như vậy, trong các bài toán về hình thang cân, ta có thể sử dụng ngay hai định lí trên để giải quyết yêu cầu đưa ra.
3. Dấu hiệu nhận biết hình thang cân
Trước tiên, ta có định lí sau:
Định lí 3: Hình thang có hai đường chéo bằng nhau là hình thang cân.
Chứng minh:
Xét hình thang \(ABCD\) (\(AB\)//\(CD\)). Giả sử \(AC=BD\).
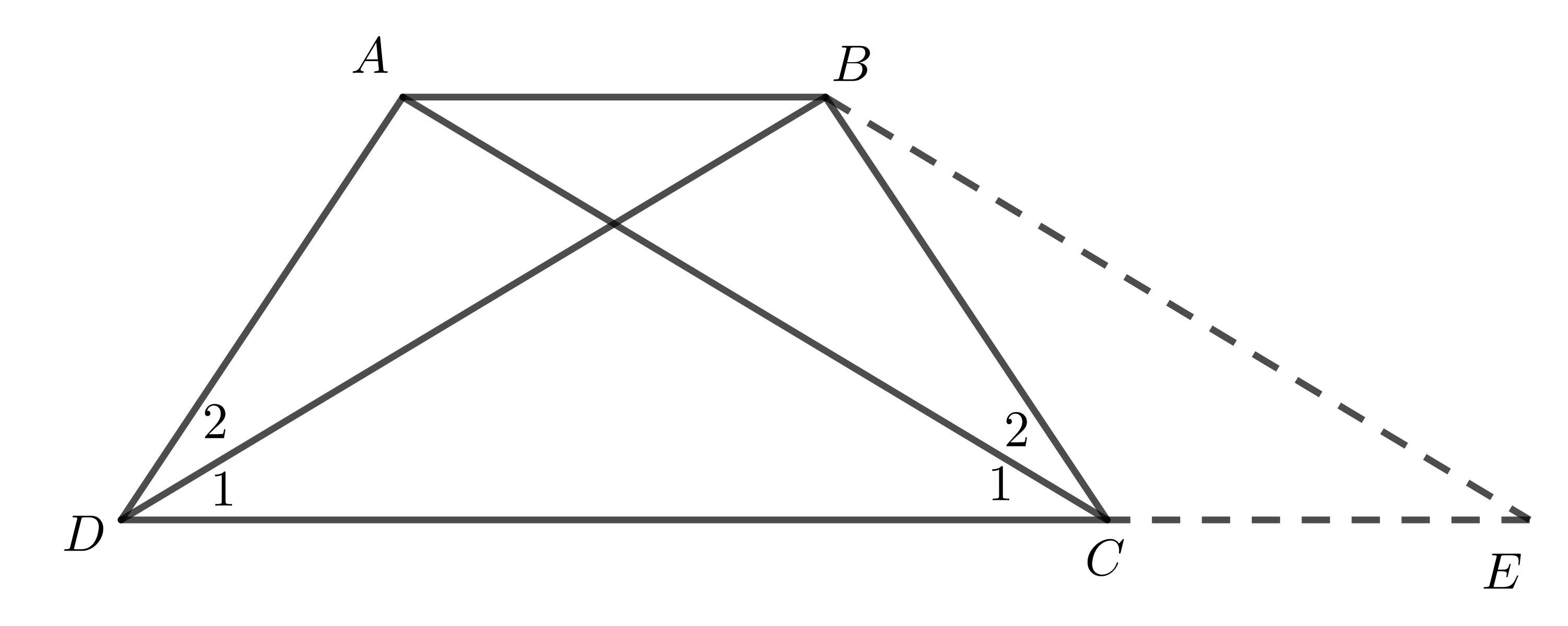
Qua \(B\) kẻ đường thẳng song song với \(AC\), cắt đường thẳng \(CD\) tại \(E\).
Do \(AB\)//\(CE\) nên \(ABEC\) là hình thang, mà \(BE\)//\(AC\) \(\Rightarrow BE=AC\)
\(\Rightarrow BE=BD\Rightarrow\Delta BDE\) cân tại \(B\Rightarrow\widehat{D_1}=\widehat{E}\).
Mặt khác, do \(BE\)//\(AC\) nên \(\widehat{E}=\widehat{C_1}\) (hai góc so le trong) \(\Rightarrow\widehat{C_1}=\widehat{D_1}\).
Xét \(\Delta ACD\) và \(\Delta BDC\) có:
- \(AC=BD\) (giả thiết);
- \(\widehat{C_1}=\widehat{D_1}\);
- \(CD\) chung
\(\Rightarrow\Delta ACD=\Delta BDC\) (cạnh - góc - cạnh) \(\Rightarrow\widehat{ADC}=\widehat{BCD}\) (hai góc tương ứng)
\(\Rightarrow ABCD\) là hình thang cân (Điều phải chứng minh).
Tổng quát: Để chứng minh một tứ giác là hình thang cân, ta cần chứng minh:
- Tứ giác đó là hình thang và có hai góc kề một đáy bằng nhau.
- Tứ giác đó là hình thang và có hai đường chéo bằng nhau.
@591438@