Bài 10: Đường thẳng song song với một đường thẳng cho trước

1. Khoảng cách giữa hai đường thẳng song song

Bài toán: Cho hai đường thẳng \(a,b\) song song. Lấy \(A,B\) bất kì thuộc \(a\). Dựng \(AH,BK\) vuông góc \(b\). Đặt \(AH=h\).

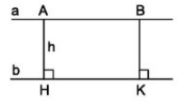
Bằng định nghĩa, ta chứng minh được \(ABKH\) là hình chữ nhật, do đó \(BK=AH=h\).

Như vậy, mọi điểm trên đường thẳng \(a\) cách đường thẳng \(b\) một khoảng bằng \(h\). Tương tự mọi điểm trên đường thẳng \(b\) cũng cắt đường thẳng \(a\) một khoảng bằng \(h\).

Ta nói: \(h\) là khoảng cách giữa hai đường thẳng song song \(a\) và \(b\).

Định nghĩa: Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia.

2. Tính chất của các điểm cách đều một đường thẳng cho trước

Bài toán: Cho đường thẳng \(b\). Hai đường thẳng \(a,a'\) nằm về hai nửa mặt phẳng \(\text{(I)}\) và \(\text{(II)}\) bờ \(b\) và cùng cách \(b\) một khoảng bằng \(h\). Lấy \(M\in\left(I\right),M'\in\left(II\right)\) sao cho \(M,M'\) cũng cách \(b\) một khoảng bằng \(h\).

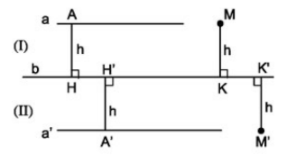
Ta có: \(AHKM\) có hai cạnh đối \(AH,MK\) vừa song song vừa bằng nhau nên \(AHKM\) là hình bình hành; mà \(\widehat{AHK}=90^0\) \(\Rightarrow AHKM\) là hình chữ nhật.

Do đó \(AM\)//\(b\), mà \(a\)//\(b\) nên \(AM\equiv a\Rightarrow M\in a\).

Hoàn toàn tương tự ta có \(M'\in a'\).

Từ kết quả bài toán trên, ta có tính chất:

Tính chất: Các điểm cách đường thẳng \(b\) một khoảng bằng \(h\) nằm trên hai đường thẳng song song với \(b\) và cách \(b\) một khoảng bằng \(h\).

Từ định nghĩa khoảng cách giữa hai đường thẳng song song và tính chất trên, ta rút ra nhận xét:

Nhận xét: Tập hợp các điểm cách đường thẳng cố định một khoảng \(h\) không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng \(h\).

3. Đường thẳng song song cách đều

Xét hình vẽ: 

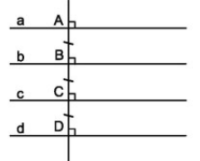
Trong hình vẽ trên, các đường thẳng \(a,b,c,d\) song song với nhau và khoảng cách giữa các đường thẳng \(a\) và \(b\), \(b\) và \(c\), \(c\) và \(d\) bằng nhau. Ta gọi chúng là các đường thẳng song song cách đều.

Ta có định lí:

• Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.
• Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.

Cụ thể: 

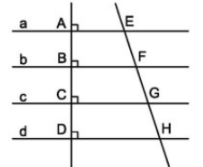
Trong hình vẽ trên, các đường thẳng \(a,b,c,d\) song song và cùng cắt đường thẳng đi qua các điểm \(E,F,G,H\).

• Nếu \(a,b,c,d\) song song cách đều thì ta có \(EF=FG=GH\).
• Ngược lại, nếu\( EF=FG=GH\) thì \(a,b,c,d\) song song cách đều.