Bài 9: Hình chữ nhật

1. Định nghĩa

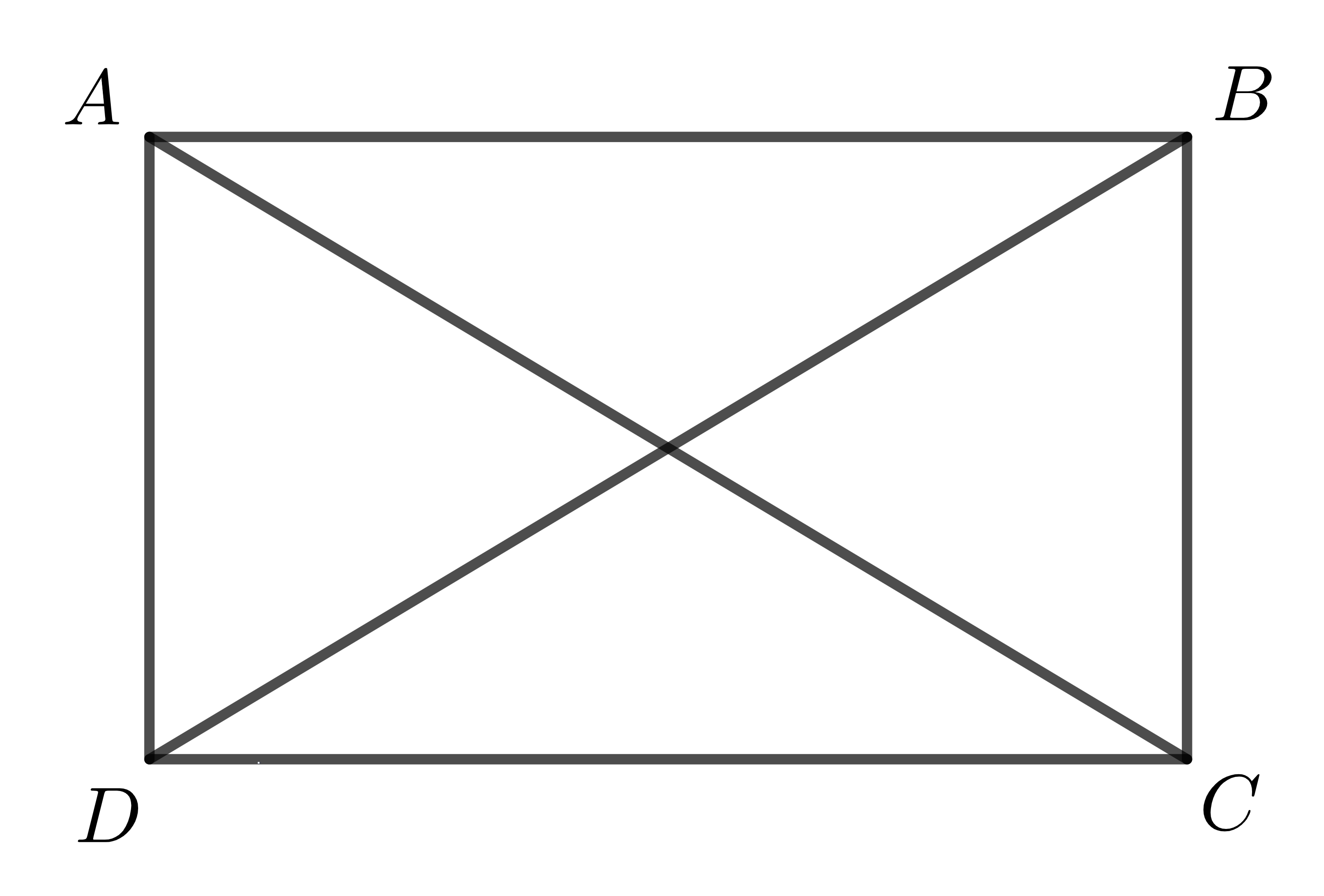
Cho tứ giác \(ABCD\) như hình vẽ sau:

Tứ giác \(ABCD\) có \(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^0\). Ta gọi tứ giác \(ABCD\) là một hình chữ nhật.

Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.

Tứ giác \(ABCD\) là hình chữ nhật \(\Leftrightarrow\) \(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^0\).

Nhận xét: Hình chữ nhật cũng là một hình bình hành, cũng là một hình thang cân.

Thật vậy: Xét hình chữ nhật \(ABCD\).

Ta có: \(\widehat{A}+\widehat{D}=180^0\) \(\Rightarrow AB\)//\(CD\) \(\Rightarrow ABCD\) là hình thang mà \(\widehat{D}=\widehat{C}\) nên \(ABCD\) là hình thang cân.

Lại có: \(\widehat{A}+\widehat{B}=180^0\Rightarrow AD\)//\(BC\Rightarrow ABCD\) là hình bình hành (các cạnh đối song song).

2. Tính chất

Ở trên ta đã biết, hình chữ nhật cũng là hình bình hành và hình thang cân nên nó có đầy đủ các tính chất của hình bình hành và hình thang cân:

• Các cạnh đối song song và bằng nhau.
• Hai đường chéo bằng nhau (do hình chữ nhật là hình thang cân).
• Hai đường chéo cắt nhau tại trung điểm mỗi đường (do hình chữ nhật là hình bình hành).

3. Dấu hiệu nhận biết

Để nhận biết một tứ giác là hình chữ nhật, ta có thể sử dụng các dấu hiệu sau:

1. Tứ giác có ba góc vuông là hình chữ nhật.
2. Hình thang cân có một góc vuông là hình chữ nhật.
3. Hình bình hành có một góc vuông là hình chữ nhật.
4. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

Chứng minh:

1) Xét tứ giác \(ABCD\). Giả sử \(\widehat{A}=\widehat{B}=\widehat{C}=90^0\).

Do tổng các góc của tứ giác bằng \(360^0\) nên ta suy ra \(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^0\)

\(\Rightarrow ABCD\) là hình chữ nhật.

2) Xét hình thang cân \(ABCD\) (\(AB\)//\(CD\)). Giả sử \(\widehat{A}=90^0\).

Do \(\widehat{A}+\widehat{D}=180^0\) (hai góc trong cùng phía) \(\Rightarrow\widehat{D}=90^0\Rightarrow\widehat{C}=90^0\) (hai góc ở đáy bằng nhau).

Theo dấu hiệu 1, ta suy ra \(ABCD\) là hình chữ nhật.

3) Xét hình bình hành \(ABCD\). Giả sử \(\widehat{A}=90^0\).

Ta có \(AB\)//\(CD\) \(\Rightarrow\widehat{A}+\widehat{D}=180^0\) (hai góc trong cùng phía) \(\Rightarrow\widehat{D}=90^0\).

Hoàn toàn tương tự, \(AD\)//\(BC\) \(\Rightarrow\widehat{A}+\widehat{B}=180^0\) (hai góc trong cùng phía) \(\Rightarrow\widehat{B}=90^0\).

Theo dấu hiệu 1, ta suy ra \(ABCD\) là hình chữ nhật.

4) Xét hình bình hành \(ABCD\). Giả sử \(AC=BD.\)

Ta có \(AB\)//\(CD\), \(AC=BD\) nên \(ABCD\) là hình thang cân \(\Rightarrow\widehat{ADC}=\widehat{BCD}\) (hai góc ở đáy).

Mặt khác, \(AD\)//\(BC\) \(\Rightarrow\widehat{ADC}+\widehat{BCD}=180^0\) \(\Rightarrow\widehat{ADC}=\widehat{BCD}=90^0\).

Theo dấu hiệu 2, ta suy ra \(ABCD\) là hình chữ nhật.

Ví dụ: Cho tam giác \(ABC\), đường cao \(AH\). Gọi \(I\) là trung điểm \(AC\). \(E\) là điểm đối xứng với \(H\) qua \(I\). Chứng minh \(AHCE\) là hình chữ nhật.

Lời giải:

Do \(E\) đối xứng với \(H\) qua \(I\) nên \(I\) là trung điểm \(HE\).

Mà \(I\) là trung điểm \(AC\) (giả thiết) \(\Rightarrow AHCE\) là hình bình hành.

Lại có \(\widehat{AHC}=90^0\) (do \(AH\perp BC\)). Do đó, \(AHCE\) là hình chữ nhật.

3. Áp dụng vào tam giác

Xét các bài toán sau: 

Bài toán 1: Cho tứ giác \(ABCD\) có \(\widehat{A}=90^0\), hai đường chéo cắt nhau tại trung điểm \(M\) của mỗi đường.

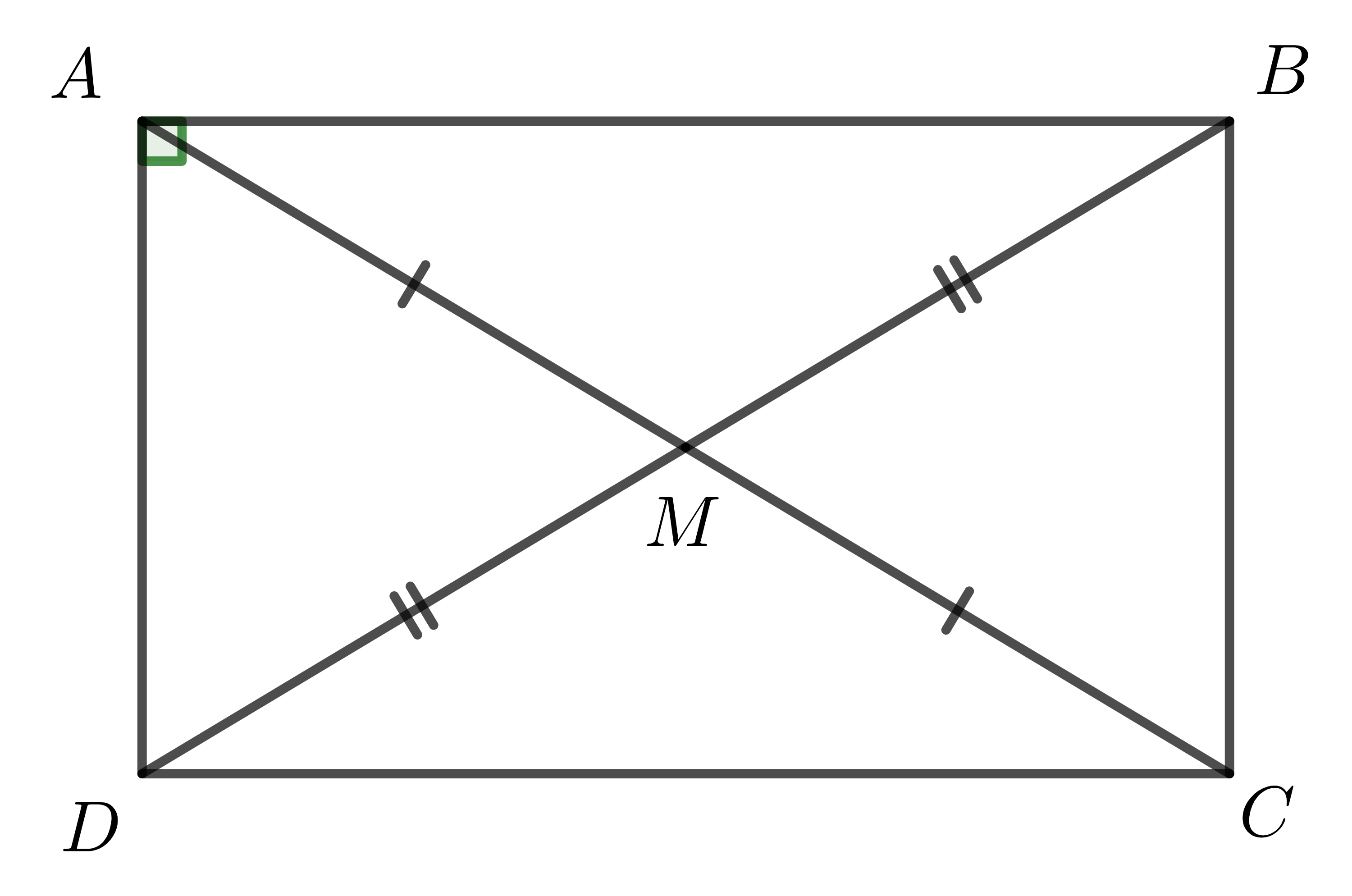
Hai đường chéo \(AC,BD\) cắt nhau tại trung điểm mỗi đường nên \(ABCD\) là hình bình hành.

Lại có \(\widehat{A}=90^0\) nên \(ABCD\) là hình chữ nhật.

\(\Rightarrow AC=BD\Rightarrow AM=BM=CM=DM\).

Tam giác \(ABD\) vuông tại \(A\), \(AM\) là đường trung tuyến ứng với cạnh huyền. Ta vừa chứng minh được \(AM=BM=DM=\dfrac{1}{2}BD\). Kết quả này không phụ thuộc vào cách chọn tứ giác \(ABCD\) thỏa mãn đề bài. 

Từ kết quả trên, ta có định lí:

Định lí: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

Bài toán 2: Xét tứ giác \(ABCD\) có các đường chéo cắt nhau tại \(M\). Biết \(MA=MB=MC=MD\).

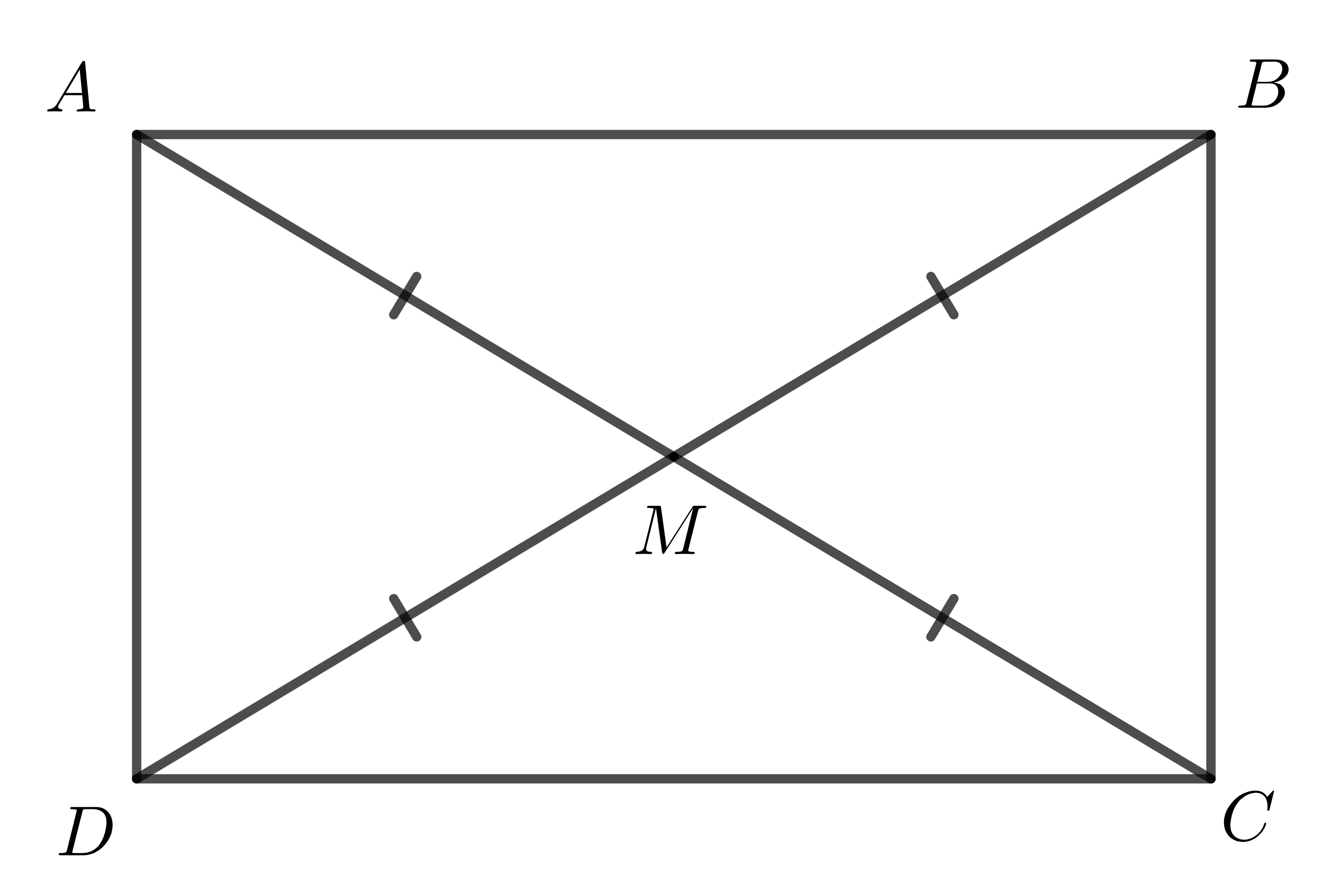
Ta có \(MA=MB=MC=MD\) nên \(M\) là trung điểm \(AC,BD\).

\(\Rightarrow ABCD\) là hình bình hành. 

Mặt khác, ta có \(MA+MC=MB+MD\Rightarrow AC=BD\).

Theo dấu hiệu 4, ta suy ra \(ABCD\) là hình chữ nhật, nên \(\widehat{A}=90^0.\)

Tam giác \(ABD\) có \(AM\) là đường trung tuyến ứng với \(BD\), và \(AM=BM=DM=\dfrac{1}{2}BD\). Ta đã chứng minh được tam giác \(ABD\) vuông tại \(A\).

Kết quả trên được phát biểu thành định lí sau:

Định lí: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng một nửa cạnh ấy thì tam giác đó là tam giác vuông.

Ví dụ: Cho tam giác \(ABC\) vuông tại \(A\), \(AB=6cm,AC=8cm\). Gọi \(M\) là trung điểm \(BC\). Tính \(AM\)?

Lời giải:

Áp dụng định lí Pytago, ta có: \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{6^2+8^2}=10\left(cm\right)\).

Do \(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) nên ta có: \(AM=\dfrac{1}{2}BC=\dfrac{1}{2}.10=5\left(cm\right).\)