Với mọi x,y>0 c/m: \(\left(x^2+y^2\right)\sqrt{x^2+y^2}\ge\sqrt{2}xy\left(x+y\right)\)

Những câu hỏi liên quan
P=\(\left(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}+\dfrac{\sqrt{x^3}-\sqrt{y^3}}{y-x}\right):\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
1 rút gọn
2 c/m P\(\ge\)0
1. ĐKXĐ : \(xy>0\)
Ta có : \(P=\left(\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}+\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{-\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}\right)\left(\dfrac{\sqrt{x}+\sqrt{y}}{x-2\sqrt{xy}+y+\sqrt{xy}}\right)\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}\left(\dfrac{\sqrt{x}+\sqrt{y}}{x-2\sqrt{xy}+y+\sqrt{xy}}\right)\)
\(=\dfrac{\left(\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)\right)\left(\sqrt{x}+\sqrt{y}\right)}{\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}\)
\(=\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\left(\sqrt{x}-\sqrt{y}\right)\left(x-\sqrt{xy}+y\right)}\)
\(=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2-\left(x+\sqrt{xy}+y\right)}{x-\sqrt{xy}+y}=\dfrac{x+2\sqrt{xy}+y-x-\sqrt{xy}-y}{x-\sqrt{xy}+y}\)
\(=\dfrac{\sqrt{xy}}{x-\sqrt{xy}+y}\)
2. Ta thấy : \(x-\sqrt{xy}+y=x-\dfrac{2.\sqrt{x}.\sqrt{y}}{2}+\dfrac{y}{4}+\dfrac{3y}{4}\)
\(=\left(\sqrt{x}-\dfrac{\sqrt{y}}{2}\right)^2+\dfrac{3y}{4}\)
Mà \(\left\{{}\begin{matrix}\left(\sqrt{x}-\dfrac{\sqrt{y}}{2}\right)^2\ge0\\\dfrac{3y}{4}\ge0\end{matrix}\right.\)
\(\Rightarrow x-\sqrt{xy}+y\ge0\)
Lại có : \(\sqrt{xy}\ge0\)
\(\Rightarrow P\ge0\) ( ĐPCM )
Đúng 1
Bình luận (0)
\(\sqrt{x^2+xy+y^2}=\sqrt{\left(x+y\right)^2-xy}\ge\sqrt{\left(x+y\right)^2-\frac{1}{4}\left(x+y\right)^2}=\frac{x+y}{2}.\sqrt{3}\)
cmtt=>\(\sqrt{x^2+xy+y^2}+\sqrt{y^2+yz+z^2}+\sqrt{z^2+zx+x^2}\ge\sqrt{3}\left(x+y+z\right)=3\)
C/m với mọi x,y>0
\(\left(1+x^2\right)\left(1+y^2\right)\ge\left(x+y\right)\left(1+xy\right)\)
1. a,b,c0 và a+b+c2017CM:Sigmadfrac{2017a-a^2}{bc}gesqrt{2}left(Sigmasqrt{dfrac{2017-a}{a}}right)2. cho x,y,z tm: x^2+y^2+z^23CM:8left(2-xright)left(2-yright)left(2-zright)geleft(x+yzright)left(y+zxright)left(z+xyright)3. a,b,c0 và a^2+b^2+c^2ge6CM:Sigmadfrac{1}{1+ab}gedfrac{3}{2}
Đọc tiếp
1. a,b,c>0 và a+b+c=2017
\(CM:\Sigma\dfrac{2017a-a^2}{bc}\ge\sqrt{2}\left(\Sigma\sqrt{\dfrac{2017-a}{a}}\right)\)
2. cho x,y,z tm: \(x^2+y^2+z^2=3\)
\(CM:8\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)\)
3. a,b,c>0 và \(a^2+b^2+c^2\ge6\)
\(CM:\Sigma\dfrac{1}{1+ab}\ge\dfrac{3}{2}\)
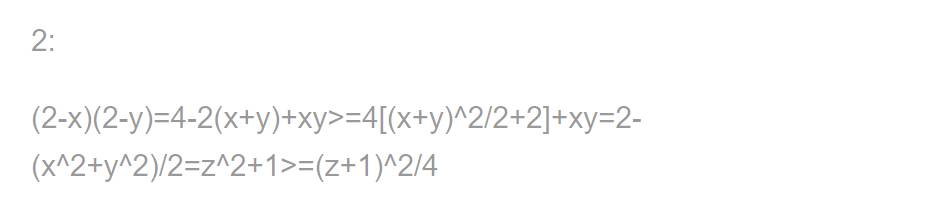
Tương tự, ta được:
\(\left(2-y\right)\left(2-z\right)>=\dfrac{\left(x+1\right)^2}{4}\)
và \(\left(2-z\right)\left(2-x\right)>=\left(\dfrac{y+1}{2}\right)^2\)
=>8(2-x)(2-y)(2-z)>=(x+1)(y+1)(z+1)
(x+yz)(y+zx)<=(x+y+yz+xz)^2/4=(x+y)^2*(z+1)^2/4<=(x^2+y^2)(z+1)^2/4
Tương tự, ta cũng co:
\(\left(y+xz\right)\left(z+y\right)< =\dfrac{\left(y^2+z^2\right)\left(x+1\right)^2}{2}\)
và \(\left(z+xy\right)\left(x+yz\right)< =\dfrac{\left(z^2+x^2\right)\left(y+1\right)^2}{2}\)
Do đó, ta được:
\(\left(x+yz\right)\left(y+zx\right)\left(z+xy\right)< =\left(x+1\right)\left(y+1\right)\left(z+1\right)\)
=>ĐPCM
Đúng 0
Bình luận (0)
Rút gọn:a/ frac{left(sqrt{x^2+9}-3right)left(sqrt{x^2+9}+3right)left(x+sqrt{xy}+yright)sqrt{x-2sqrt{xy}+y}}{xleft(xsqrt{x}-ysqrt{y}right)} (với x0, yge0, xney b/ left[left(frac{1}{sqrt{x}}+frac{1}{sqrt{y}}right).frac{2}{sqrt{x}+sqrt{y}}+frac{1}{sqrt{x}}+frac{1}{sqrt{y}}right]:frac{sqrt{x^3}+ysqrt{x}+xsqrt{y}+sqrt{y^3}}{sqrt{x^3y}+sqrt{xy^3}}(với x0 và xne1 c/ left(frac{sqrt{x}+1}{sqrt{xy}+1}+frac{sqrt{xy}+sqrt{x}}{1-sqrt{xy}}+1right):left(1-frac{sqrt{xy}+sqrt{x}}{sqrt{xy}-1}-frac{sqrt{x}+1}{sqrt...
Đọc tiếp
Rút gọn:
a/ \(\frac{\left(\sqrt{x^2+9}-3\right)\left(\sqrt{x^2+9}+3\right)\left(x+\sqrt{xy}+y\right)\sqrt{x-2\sqrt{xy}+y}}{x\left(x\sqrt{x}-y\sqrt{y}\right)}\) (với x>0, y\(\ge\)0, x\(\ne\)y
b/ \(\left[\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right).\frac{2}{\sqrt{x}+\sqrt{y}}+\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right]:\frac{\sqrt{x^3}+y\sqrt{x}+x\sqrt{y}+\sqrt{y^3}}{\sqrt{x^3y}+\sqrt{xy^3}}\)(với x>0 và x\(\ne\)1
c/ \(\left(\frac{\sqrt{x}+1}{\sqrt{xy}+1}+\frac{\sqrt{xy}+\sqrt{x}}{1-\sqrt{xy}}+1\right):\left(1-\frac{\sqrt{xy}+\sqrt{x}}{\sqrt{xy}-1}-\frac{\sqrt{x}+1}{\sqrt{xy}+1}\right)\)(với x>0 và x\(\ne\)1
ta có bđt cần chứng minh frac{sqrt{xy+z}+sqrt{2x^2+2y^2}}{1+sqrt{xy}}ge1Leftrightarrowsqrt{xy+z}+sqrt{2left(x^2+y^2right)}ge1+sqrt{xy}Áp dụng bđt bu nhi ta có sqrt{2left(x^2+y^2right)}ge x+y (1)mà x+y+z1Rightarrow xy+zxy+zleft(x+y+zright)left(z+xright)left(z+yright)áp dụng bu nhi a ta có sqrt{left(z+xright)left(z+yright)}ge z+sqrt{xy} (2)từ (1) và (2) sqrt{xy+z}+sqrt{2x^2+2y^2}ge x+y+z+sqrt{xy}1+sqrt{xy}
Đọc tiếp
ta có bđt cần chứng minh
\(\frac{\sqrt{xy+z}+\sqrt{2x^2+2y^2}}{1+\sqrt{xy}}\ge1\Leftrightarrow\sqrt{xy+z}+\sqrt{2\left(x^2+y^2\right)}\ge1+\sqrt{xy}\)
Áp dụng bđt bu nhi ta có
\(\sqrt{2\left(x^2+y^2\right)}\ge x+y\) (1)
mà x+y+z=1\(\Rightarrow xy+z=xy+z\left(x+y+z\right)=\left(z+x\right)\left(z+y\right)\)
áp dụng bu nhi a ta có \(\sqrt{\left(z+x\right)\left(z+y\right)}\ge z+\sqrt{xy}\) (2)
từ (1) và (2) => \(\sqrt{xy+z}+\sqrt{2x^2+2y^2}\ge x+y+z+\sqrt{xy}=1+\sqrt{xy}\)
Cho x, y, z >0 thoả mãn \(x^2+y^2+z^2=1\) . Cmr: \(\frac{x+y+z}{xy+yz+xz}\ge\sqrt{3}+\frac{1}{2\sqrt{3}}\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\)
Giải hệ pt
1/left{{}begin{matrix}4xsqrt{y+1}+8xleft(4x^2-4x-3right)sqrt{x+1}dfrac{x}{x+1}+x^2left(y+2right)sqrt{left(x+1right)left(y+1right)}end{matrix}right.
2/left{{}begin{matrix}xsqrt{y^2+6}+ysqrt{x^2+3}7xyxsqrt{x^2+3}+ysqrt{y^2+6}x^2+y^2+2end{matrix}right.left{{}begin{matrix}xsqrt{y^2+6}+ysqrt{x^2+3}7xyxsqrt{x^2+3}+ysqrt{y^2+6}x^2+y^2+2end{matrix}right.
3/left{{}begin{matrix}left(2x+y-1right)left(sqrt{x+3}+sqrt{xy}+sqrt{x}right)8sqrt{x}left(sqrt{x+3}+sqrt{xy}right)^2+xy2xleft(6-xright)end...
Đọc tiếp
Giải hệ pt
1/\(\left\{{}\begin{matrix}4x\sqrt{y+1}+8x=\left(4x^2-4x-3\right)\sqrt{x+1}\\\dfrac{x}{x+1}+x^2=\left(y+2\right)\sqrt{\left(x+1\right)\left(y+1\right)}\end{matrix}\right.\)
2/\(\left\{{}\begin{matrix}x\sqrt{y^2+6}+y\sqrt{x^2+3}=7xy\\x\sqrt{x^2+3}+y\sqrt{y^2+6}=x^2+y^2+2\end{matrix}\right.\)\(\left\{{}\begin{matrix}x\sqrt{y^2+6}+y\sqrt{x^2+3}=7xy\\x\sqrt{x^2+3}+y\sqrt{y^2+6}=x^2+y^2+2\end{matrix}\right.\)
3/\(\left\{{}\begin{matrix}\left(2x+y-1\right)\left(\sqrt{x+3}+\sqrt{xy}+\sqrt{x}\right)=8\sqrt{x}\\\left(\sqrt{x+3}+\sqrt{xy}\right)^2+xy=2x\left(6-x\right)\end{matrix}\right.\)\(\left\{{}\begin{matrix}\left(2x+y-1\right)\left(\sqrt{x+3}+\sqrt{xy}+\sqrt{x}\right)=8\sqrt{x}\\\left(\sqrt{x+3}+\sqrt{xy}\right)^2+xy=2x\left(6-x\right)\end{matrix}\right.\)
4/\(\left\{{}\begin{matrix}\sqrt{xy+x+2}+\sqrt{x^2+x}-4\sqrt{x}=0\\xy+x^2+2=x\left(\sqrt{xy+2}+3\right)\end{matrix}\right.\)\(\left\{{}\begin{matrix}\sqrt{xy+x+2}+\sqrt{x^2+x}-4\sqrt{x}=0\\xy+x^2+2=x\left(\sqrt{xy+2}+3\right)\end{matrix}\right.\)
m.n giúp e mấy bài này vs ạ!!
Với mọi a, b, c, x, y, z \(\in\) R, chứng minh : \(\sqrt{a^2+x^2}+\sqrt{b^2+y^2}+\sqrt{c^2+z^2}\ge\sqrt{\left(a+b+c\right)^2+\left(x+y+z\right)^2}\)
Ta sẽ chứng minh:
\(\sqrt{a^2+x^2}+\sqrt{b^2+y^2}\ge\sqrt{\left(a+b\right)^2+\left(x+y\right)^2}\)
Thật vậy, bình phương 2 vế, BĐT tương đương:
\(a^2+x^2+b^2+y^2+2\sqrt{a^2b^2+x^2y^2+a^2y^2+b^2x^2}\ge a^2+b^2+x^2+y^2+2ab+2xy\)
\(\Leftrightarrow\sqrt{a^2b^2+x^2y^2+a^2y^2+b^2x^2}\ge ab+xy\)
\(\Leftrightarrow a^2b^2+x^2y^2+a^2y^2+b^2x^2\ge a^2b^2+x^2y^2+2abxy\)
\(\Leftrightarrow a^2y^2+b^2x^2-2abxy\ge0\)
\(\Leftrightarrow\left(ay-bx\right)^2\ge0\) (luôn đúng)
Áp dụng:
\(VT=\sqrt{a^2+x^2}+\sqrt{b^2+y^2}+\sqrt{c^2+z^2}\)
\(VT\ge\sqrt{\left(a+b\right)^2+\left(x+y\right)^2}+\sqrt{c^2+z^2}\ge\sqrt{\left(a+b+c\right)^2+\left(x+y+z\right)^2}\) (đpcm)
Đúng 0
Bình luận (0)















