ΔABC cân tại A.AH⊥BC,AB=5cm,BC=8cm,G∈AHsao cho AH=\(\frac{1}{2}\)AG.Tính độ dài AM,BG
Cho ΔABC cân có AB = AC = 5cm, BC = 8cm. Kẻ AH vuông góc BC (HBC) a. Chứng minh: HB = HC. b. Tính độ dài AH. c. Kẻ HD vuông góc với AB (D∈AB), kẻ HE vuông góc với AC (E∈AC). Chứng minh ΔHDE cân.
a: Xét ΔABC cân tại A có AH là đường cao
nên H là trung điểm của BC
hay HB=HC
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
Cho Δ A B C cân tại A, trung tuyến AM. Biết B C = 24 c m , A M = 5 c m . Tính độ dài các cạnh AB và AC.
A. A B = A C = 13 c m
B. A B = A C = 14 c m
C. A B = A C = 15 c m
D. A B = A C = 16 c m
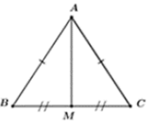
Δ A B C cân tại A (gt) mà AM là trung tuyến nên AM cũng là đường cao của tam giác đó.
Vì AM là trung tuyến của Δ A B C nên M là trung điểm của BC
⇒ B M = B C 2 = 24 : 2 = 12 c m

Bài 6. Cho ΔABC có AB = AC = 5cm, BC = 8cm. Kẻ AH vuông góc BC (H thuộc BC).
a) Chứng minh: HB = HC ̂
b) Tính độ dài đoạn AH?
c) Kẻ HD vuông góc AB (D thuộc AB), HE vuông góc AC (E thuộc AC). Chứng minh: ΔHDE cân.
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(gt)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: HB=HC(hai cạnh tương ứng)
b) Ta có: HB=HC(cmt)
mà HB+HC=BC(H nằm giữa B và C)
nên \(HB=HC=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=AB^2-BH^2=5^2-4^2=9\)
hay AH=3(cm)
Vậy: AH=3cm
c) Xét ΔABC có AB=AC(gt)
nên ΔABC cân tại A(Định nghĩa tam giác cân)
Ta có: ΔABC cân tại A(cmt)
nên \(\widehat{B}=\widehat{C}\)(hai góc ở đáy)
Xét ΔDBH vuông tại D và ΔECH vuông tại E có
HB=HC(cmt)
\(\widehat{B}=\widehat{C}\)(cmt)Do đó: ΔDBH=ΔECH(cạnh huyền-góc nhọn)
⇒HD=HE(Hai cạnh tương ứng)
Xét ΔHDE có HD=HE(cmt)
nên ΔHDE cân tại H(Định nghĩa tam giác cân)
Bài 1: Cho tam giác ABC cân tại B, kẻ CH vuông góc AB. Biết AH= 1cm, BH= 4cm. Tính độ dài AC.
Bài 2: Cho tam giác ABC vuông tại A. Cạnh AB= 5cm đường cao AH, BH= 3cm, CH= 8cm. Tính AC.
Bài 3: Cho tam giác ABC vuông tại A, có \(\frac{AB}{BC}=\frac{3}{5}\)và AC= 16cm. Tính độ dài các cạnh AB=BC.
Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC
Cho ΔABC cân tại A(BC>AB) có đường trung tuyến AI và trọng tâm G.
a, Biết AB=5cm;BC=8cm. Tính đôi dài của các đoạn thẳng AI,BG.
b, M∈tia đối của tia AC, AM=AB.N∈tia đối của tia CA, CN=CB. C/minh BN>BM
a) Ta có: ΔABC cân tại A(gt)
mà AI là đường trung tuyến ứng với cạnh đáy BC(gt)
nên AI là đường cao ứng với cạnh BC(Định lí tam giác cân)
hay AI\(\perp\)BC
Ta có: I là trung điểm của BC(gt)
nên \(BI=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABI vuông tại I, ta được:
\(AI^2+BI^2=AB^2\)
\(\Leftrightarrow AI^2=AB^2-BI^2=5^2-4^2=9\)
hay AI=3(cm)
Vậy: AI=3cm
Bài 3: Cho ΔABC cân có AB = AC = 5cm, BC = 8cm. Kẻ AH vuông góc BC (H thuộc BC)
a. Chứng minh: HB = HC.
b. Tính độ dài AH.
c. Kẻ HD vuông góc với AB (D∈AB), kẻ HE vuông góc với AC (E∈AC).
Chứng minh ΔHDE cân.
d) So sánh HD và HC.
Bài 4. Cho tam giác ABC có AB = AC = 5cm, BC = 6cm. Đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC.
a) Chứng minh ΔAMB = ΔAMC và AM là tia phân giác của góc A.
b) Chứng minh AM
c) Tính độ dài các đoạn thẳng BM và AM.
d) Từ M vẽ ME AB (E thuộc AB) và MF AC (F thuộc AC). Tam giác MEF là tam giác gì? Vì sao?
Bài 3:
a) Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC(ΔABC cân tại A)
AH chung
Do đó: ΔABH=ΔACH(cạnh huyền-cạnh góc vuông)
Suy ra: BH=CH(hai cạnh tương ứng)
b) Ta có: BH=CH(cmt)
mà BH+CH=BC(H nằm giữa B và C)
nên \(BH=CH=\dfrac{BC}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AH^2=AB^2-BH^2=5^2-4^2=9\)
hay AH=3(cm)
Vậy: AH=3(cm)
c) Xét ΔDBH vuông tại D và ΔECH vuông tại E có
BH=CH(cmt)
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
Do đó: ΔDBH=ΔECH(cạnh huyền-góc nhọn)
Suy ra: HD=HE(hai cạnh tương ứng)
Xét ΔHDE có HD=HE(cmt)
nên ΔHDE cân tại H(Định nghĩa tam giác cân)
Bài 4:
a) Xét ΔAMB và ΔAMC có
AM chung
MB=MC(M là trung điểm của BC)
AB=AC(ΔBAC cân tại A)
Do đó: ΔAMB=ΔAMC(c-c-c)
Suy ra: \(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
hay AM là tia phân giác của \(\widehat{BAC}\)(đpcm)
b) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MB=MC(M là trung điểm của BC)
nên M nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
hay AM\(\perp\)BC
c) Ta có: BM=CM(M là trung điểm của BC)
nên \(BM=CM=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABM vuông tại M, ta được:
\(AB^2=AM^2+BM^2\)
\(\Leftrightarrow AM^2=AB^2-BM^2\)
\(\Leftrightarrow AM^2=5^2-3^2=16\)
hay AM=4(cm)
Vậy: BM=3cm; AM=4cm
Bài1:Cho ΔMNP vuông tại N. Tính độ dài MN biết MP=√30cm,NP=√14 cm
Bài2:Cho ΔABC cân tại A. Biết AB=2cm. Tính BC
Bài3:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=6cm,HB=4cm,HC=9cm
Bài4:Cho ΔABC vuông tại A,AH⊥BC tại H. Tính độ dài các cạnh của ΔABC biết AH=4cm,HB=2cm,HC=8cm
Bài5:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=4cm,HB=2cm,HC=8cm.Tính BC,AH,AC
Bài6:Cho ΔABC vuông tại A,AH⊥BC tại H.Biết AB=6cm,AC=8cm và \(\dfrac{HB}{HC}\)=\(\dfrac{9}{16}\)Tính HB,HC
Bài 3:
\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)
BC=13cm
=>\(AC=3\sqrt{13}\left(cm\right)\)
- Áp dụng định lý pi ta go vào tam giác ABC vuông tại A ta được :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow AC^2+5^2=13^2\)
\(\Rightarrow AC=12\left(cm\right)\)
- Xét tam giác BHA và tam giác BAC có : \(\left\{{}\begin{matrix}\widehat{BHA}=\widehat{BAC}=90^o\\\widehat{B}\left(chung\right)\end{matrix}\right.\)
=> Hai tam giác trên đồng dạng .
=> \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
=> \(BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\)
=> \(CH=BC-BH=\dfrac{144}{13}\left(cm\right)\)
- Áp dụng định lý pi ta go vào tam giác ABH vuông tại H ta được :
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH=\dfrac{60}{13}\left(cm\right)\)
Vậy ...
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=13^2-5^2=144\)
hay AC=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot13=5\cdot12\)
\(\Leftrightarrow AH\cdot13=60\)
hay \(AH=\dfrac{60}{13}cm\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=BH^2+AH^2\)
\(\Leftrightarrow BH^2=AB^2-AH^2=5^2-\left(\dfrac{60}{13}\right)^2=\dfrac{625}{169}\)
hay \(BH=\dfrac{25}{13}cm\)
Ta có: BH+CH=BC(H nằm giữa B và C)
\(\Leftrightarrow CH=BC-BH=13-\dfrac{25}{13}\)
hay \(CH=\dfrac{144}{13}cm\)
Vậy: AC=12cm; \(AH=\dfrac{60}{13}cm\); \(BH=\dfrac{25}{13}cm\); \(CH=\dfrac{144}{13}cm\)
1. Cho ΔABC cân tại A có BC= 5cm, B = C = 40° . Tính AB và đường cao AH.
2. Cho hình vẽ biết B = 60°, AH = 5, BC = 10. Tính AB, AC

1) Mình làm rồi nhé:
https://hoc24.vn/cau-hoi/cho-dabc-can-tai-a-co-bc-5cm-b-c-40-tinh-ab-va-duong-cao-ah.8311486416239
2) Xét tam giác vuông ABH ta có:
\(cosB=\dfrac{AH}{AB}\)
\(\Rightarrow cos60^o=\dfrac{5}{AB}\Rightarrow AB=\dfrac{5}{cos60^o}=10\)
Áp dụng định lý Py-ta-go vào tam giác này ta có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{10^2-5^2}=5\sqrt{3}\)
Mà: \(BH+CH=BC\)
\(\Rightarrow CH=BC-BH=10-5\sqrt{3}\approx1,3\)
Áp dụng định lý Py-ta-go ta có:
\(AC=\sqrt{CH^2+AH^2}=\sqrt{1,3^2+5^2}\approx5,2\)