Tìm các số thực x,y khác 0 thỏa mãn: \(x-2xy+2y^2-2y^2-2x+6y+5=0\)

Những câu hỏi liên quan
Tìm các số thực x,y khác 0 thỏa mãn: \(x^2-2xy+y^2-2x+6y+5=0\)
Tìm các số thực x,y,z thỏa mãn (x−1)^2 +|3y−1|+|z+2| = 0.
Ta có: \(\left(x-1\right)^2\ge0\forall x\)
\(\left|3y-1\right|\ge0\forall y\)
\(\left|z+2\right|\ge0\forall z\)
Do đó: \(\left(x-1\right)^2+\left|3y-1\right|+\left|z+2\right|\ge0\forall x,y,z\)
Dấu '=' xảy ra khi \(\left(x,y,z\right)=\left(1;\dfrac{1}{3};-2\right)\)
Đúng 0
Bình luận (0)
tìm các cặp số x,y thỏa mãn x^2+5y^2-4xy-6y+4=0
\(\Leftrightarrow\left(x^2-4xy+4y^2\right)+\left(y^2-6y+9\right)=5\)
\(\Leftrightarrow\left(x-2y\right)^2+\left(y-3\right)^2=5\)
\(\Leftrightarrow\left(x-2y\right)^2=5-\left(y-3\right)^2\) (1)
Do \(\left(x-2y\right)^2\ge0;\forall x;y\)
\(\Rightarrow5-\left(y-3\right)^2\ge0\Rightarrow\left(y-3\right)^2\le5\)
\(\Rightarrow\left[{}\begin{matrix}\left(y-3\right)^2=0\\\left(y-3\right)^2=1\\\left(y-3\right)^2=4\end{matrix}\right.\)
Thay vào (1):
- Với \(\left(y-3\right)^2=0\) \(\Rightarrow\left(x-2y\right)^2=5\) vô nghiệm do 5 ko phải SCP
- Với \(\left(y-3\right)^2=1\Rightarrow\left[{}\begin{matrix}y=4\\y=2\end{matrix}\right.\)
\(y=4\Rightarrow\left(x-8\right)^2=4\Rightarrow\left[{}\begin{matrix}x=10\\x=6\end{matrix}\right.\)
\(y=2\Rightarrow\left(x-4\right)^2=4\Rightarrow\left[{}\begin{matrix}x=6\\x=2\end{matrix}\right.\)
- Với \(\left(y-3\right)^2=4\Rightarrow\left[{}\begin{matrix}y=5\\y=1\end{matrix}\right.\)
\(y=5\Rightarrow\left(x-10\right)^2=1\Rightarrow\left[{}\begin{matrix}x=11\\x=9\end{matrix}\right.\)
\(y=1\Rightarrow\left(x-2\right)^2=1\Rightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
Em tự kết luận các cặp nghiệm
Đúng 2
Bình luận (1)
Chắc phải là cặp số nguyên chứ có vô số cặp x;y bất kì thỏa mãn pt này
Đúng 1
Bình luận (1)
Cho các số dương x, y thỏa mãn: \(7x^2-13xy-2y^2=0\). Tính \(A=\frac{2x-6y}{7x+4y}\).
Tìm các số thực x,y,z thỏa mãn (x−1)2 +|3y−1|+|z+2| = 0.
Hãy giúp mk.TKS mn
`(x-1)^2>=0`
`|3y-1|>=0`
`|z+2|>=0`
`=>(x-1)^2+|3y-1|+|z+2|>=0`
Mà đề bài cho =0
`=>{(x-1=0),(3y-1=0),(z+2=0):}`
`=>{(x=1),(y=1/3),(z=-2):}`
Vậy `x=1` và `y=1/3` và `z=-2`
Đúng 1
Bình luận (1)
Ta có: \(\left(x-1\right)^2\ge0\forall x\)
\(\left|3y-1\right|\ge0\forall y\)
\(\left|z+2\right|\ge0\forall z\)
Do đó: \(\left(x-1\right)^2+\left|3y-1\right|+\left|z+2\right|\ge0\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-1=0\\3y-1=0\\z+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{1}{3}\\z=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho x và y thỏa mãn: x^2 + 2xy + 6x + 6y + 2y^2 + 8=0.Tìm giá trị LN và NN của biểu thức B= x + y + 2016.
Cho x,y,z là các số thực thỏa mãn 2x=3y=5z và |x-2y|=5.Tìm GTNN của 3x-2z
Các số thực x, y thỏa mãn: (x + 2y) + (2x - y)i = 6 + 7i. Giá trị biểu thức T = x + y bằng:
A. 4
B. 5
C. 6
D. 7
Ta có: (x + 2y) + (2x - y)i = 6 + 7i
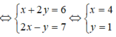
Vậy: T = 4 + 1 = 5
Chọn B
Đúng 0
Bình luận (0)
Cho các số dương x, y thỏa mãn:\(7x^2-13xy-2y^2=0\)
Tính: \(A=\frac{2x-6y}{7x+4y}\)
Các cậu giúp hộ ạ !!!
ta có \(7x^2-13xy-2y^2=0\)
\(7x^2-14xy+xy-2y^2=0\)
7x(x-2y)+y(x-2y)=0
(7x+y)(x-2y)=0
=>. 7x+y=0 hoặc x-2y=0
=> y=-7x hoặc x=2y
Thay lần lượt vào A là OK nha bn !
Đúng 0
Bình luận (0)


















