Cho tam giác ABC vuông tại A, đường cao AH biết BH=9, HC=6 . Tính góc B, góc C

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9; HC = 16. Tính độ dài các đoạn thẳng AH, AB, AC, số đo góc B, góc C?
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 49cm, HC=16cm
Tính góc B,C
Bài 1 Cho tam giác ABC vuông tại A có đường cao AH .biết BH = 9 cm ,HC = 16 cm .tính AH; AC ;số đo góc ABC (số đo góc làm tròn đến độ)
bài 2 Cho tam giác ABC vuông tại A , đường cao AH. biết AB = 3 cm ,AC = 4 cm. Tính độ dài các cạnh BC, AH và số đo góc ACB (làm tròn đến độ)
Bài 1:
AH=12cm
AC=20cm
\(\widehat{ABC}=37^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, biết HB 9; HC 16. Tính góc B và góc C. A.
B
^
53
0
8
;
C
^
36
0
52
B.
B
^
36
0
52...
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH, biết HB = 9; HC = 16. Tính góc B và góc C.
A. B ^ = 53 0 8 ' ; C ^ = 36 0 52 '
B. B ^ = 36 0 52 ' ; C ^ = 53 0 8 '
C. B ^ = 48 0 35 ' ; C ^ = 41 0 25 '
D. B ^ = 41 0 25 ' ; C ^ = 48 0 35 '
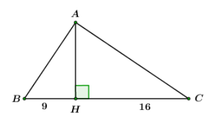
Ta có: BC = BH + CH = 9 + 16 = 25
Áp dụng hệ thức lượng cho ABC vuông tại A có đường cao AH ta có:
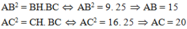
Xét ABC vuông tại A ta có:
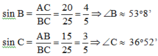
Đáp án cần chọn là: A
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A đường cao AH, AB=6, BC=10 a) Tính BH, HC, AH, góc BAH. b) Vẽ BD là tia phân giác của tam giác ABH ( D thuộc AC ). Kẻ AK vuông góc với BD tại K. Cmr: BH.BC=BK.BD. c) BD cắt AH tại S. Tính diện tích tứ giác SHCD?
b: Xét ΔACB vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\left(1\right)\)
Xét ΔABK vuông tại A có AK là đường cao
nên \(AB^2=BK\cdot BD\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=BK\cdot BD\)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại B đường cao BH cho AH=9 cm, HC=16 cm
a) tính BH,AB,BC
b)từ H kẻ HE vuông góc BC .chứng minh BE.BC=HA.HC
c)trung tuyến BM của tam giác ABC .Tính góc BMH
d0 Tia phân giác góc ABC cắt AC tại D. CM: 1/BA + 1/BC = (căn 2)/BD
b: Xét ΔBAC vuông tại B có BH là đường cao
nên \(HA\cdot HC=BH^2\left(1\right)\)
Xét ΔBHC vuông tại H có HE là đường cao
nên \(BE\cdot BC=BH^2\left(2\right)\)
Từ (1) và (2) suy ra \(HA\cdot HC=BE\cdot BC\)
Đúng 3
Bình luận (1)
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH. a) Biết AB 9cm, BC 15cm. Tính BH, HC b) Biết BH 1cm, HC 3cm. Tính AB, AC c) Biết AB 6cm, AC 8cm. Tính AH, BCBài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB 3cm, BH 2,4cm a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc BBài 3: Cho tam giác ABC có BC 9cm, góc B 60 độ, góc C 40 độ, đường cao AH. Tính AH, AB, AC
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A, đường cao AH.
a) Biết AB= 9cm, BC= 15cm. Tính BH, HC
b) Biết BH= 1cm, HC= 3cm. Tính AB, AC
c) Biết AB= 6cm, AC= 8cm. Tính AH, BC
Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB= 3cm, BH= 2,4cm
a) Tính BC, AC, AH, HC b) Tính tỉ số lượng giác của góc B
Bài 3: Cho tam giác ABC có BC= 9cm, góc B= 60 độ, góc C= 40 độ, đường cao AH. Tính AH, AB, AC
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
cho tam giác ABC vuông tại A có AH là đường cao . Biết BH= 9 cm , AB = 15 cm . tính BC , AC, HC , số đo góc ABC
Theo hệ thức lượng trong tam giác vuông ta có
\(15^2=9\cdot BC\)
\(BC=\frac{225}{9}=25\left(cm\right)\)
\(\Rightarrow9+HC=25\Rightarrow HC=16\left(cm\right)\)
Theo định lý Pytago ta có
\(AC=\sqrt{BC^2-AB^2}=\sqrt{400}=20\left(cm\right)\)
Ta có đặt \(\widehat{ABC}=\alpha\)
\(\sin\alpha=\frac{20}{25}=0,8\)
Tới đây mình chịu do kết quả nó hơi kỳ...
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a đường cao ah có bh=2 và hc=6 a,tính ah,ac,ab b, gọi k là truung điểm của ac tính góc akb
a, \(BC=BH+HC=8\)
Áp dụng HTL:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=16\\AC^2=CH\cdot BC=48\\AH^2=CH\cdot BC=12\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=4\left(cm\right)\\AC=4\sqrt{3}\left(cm\right)\\AH=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
\(b,\) Vì K là trung điểm AC nên \(AK=\dfrac{1}{2}AC=2\sqrt{3}\left(cm\right)\)
Ta có \(\tan\widehat{AKB}=\dfrac{AB}{AK}=\dfrac{4}{2\sqrt{3}}=\dfrac{2\sqrt{3}}{3}\approx\tan49^0\)
\(\Rightarrow\widehat{AKB}\approx49^0\)
Đúng 0
Bình luận (0)
Cho một tam giác ABC vuông tại A có widehat{B}dfrac{1}{2}widehat{C}. Kẻ đường cao AH sao cho cạnh AH vuông góc với cạnh huyền BC tại H. Các hình chiếu của AB và AC trên BC lần lượt là BH và HC. Biết HC 1,6cm.
a) Tính góc B và C, và các tỉ số lượng giác của chúng nó.
b*) Tính độ dài các cạnh BC, AB và AC.
Gợi ý: Sử dụng các hệ thức về tỉ số lượng giác của góc nhọn và một trong bốn hệ thức về cạnh góc vuông và đường cao trong tam giác vuông để tính.
c) Tính độ dài các cạnh AH và BH.
d) Hãy c...
Đọc tiếp
Cho một tam giác ABC vuông tại A có \(\widehat{B}=\dfrac{1}{2}\widehat{C}\). Kẻ đường cao AH sao cho cạnh AH vuông góc với cạnh huyền BC tại H. Các hình chiếu của AB và AC trên BC lần lượt là BH và HC. Biết HC = 1,6cm.
a) Tính góc B và C, và các tỉ số lượng giác của chúng nó.
b*) Tính độ dài các cạnh BC, AB và AC.
Gợi ý: Sử dụng các hệ thức về tỉ số lượng giác của góc nhọn và một trong bốn hệ thức về cạnh góc vuông và đường cao trong tam giác vuông để tính.
c) Tính độ dài các cạnh AH và BH.
d) Hãy chứng minh rằng: Cả ba tam giác vuông ABC, HBA và HAC đồng dạng với nhau.
e*) Chứng minh rằng: \(\dfrac{\sin\widehat{HAC}}{\cos\widehat{HBA}}\div\dfrac{\tan\widehat{HAC}}{\cot\widehat{ABC}}=\dfrac{csc^2\widehat{ABC}}{sec^2\widehat{ABC}\cdot\cot\widehat{HBA}}\)
Gợi ý:
1. Secant - sec α nghịch đảo với cos α
2. Cosecant - csc α nghịch đảo với sin α





















