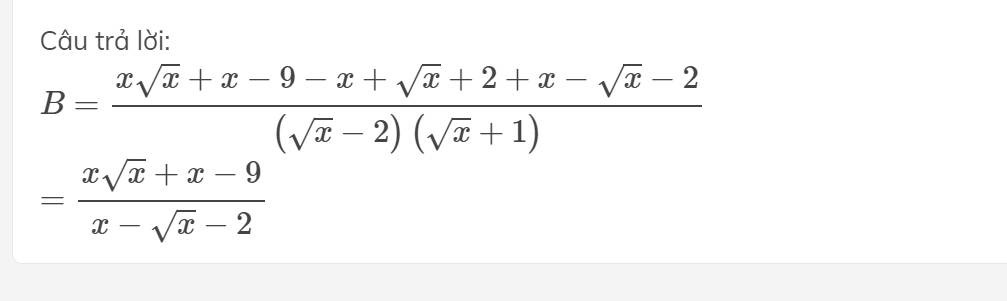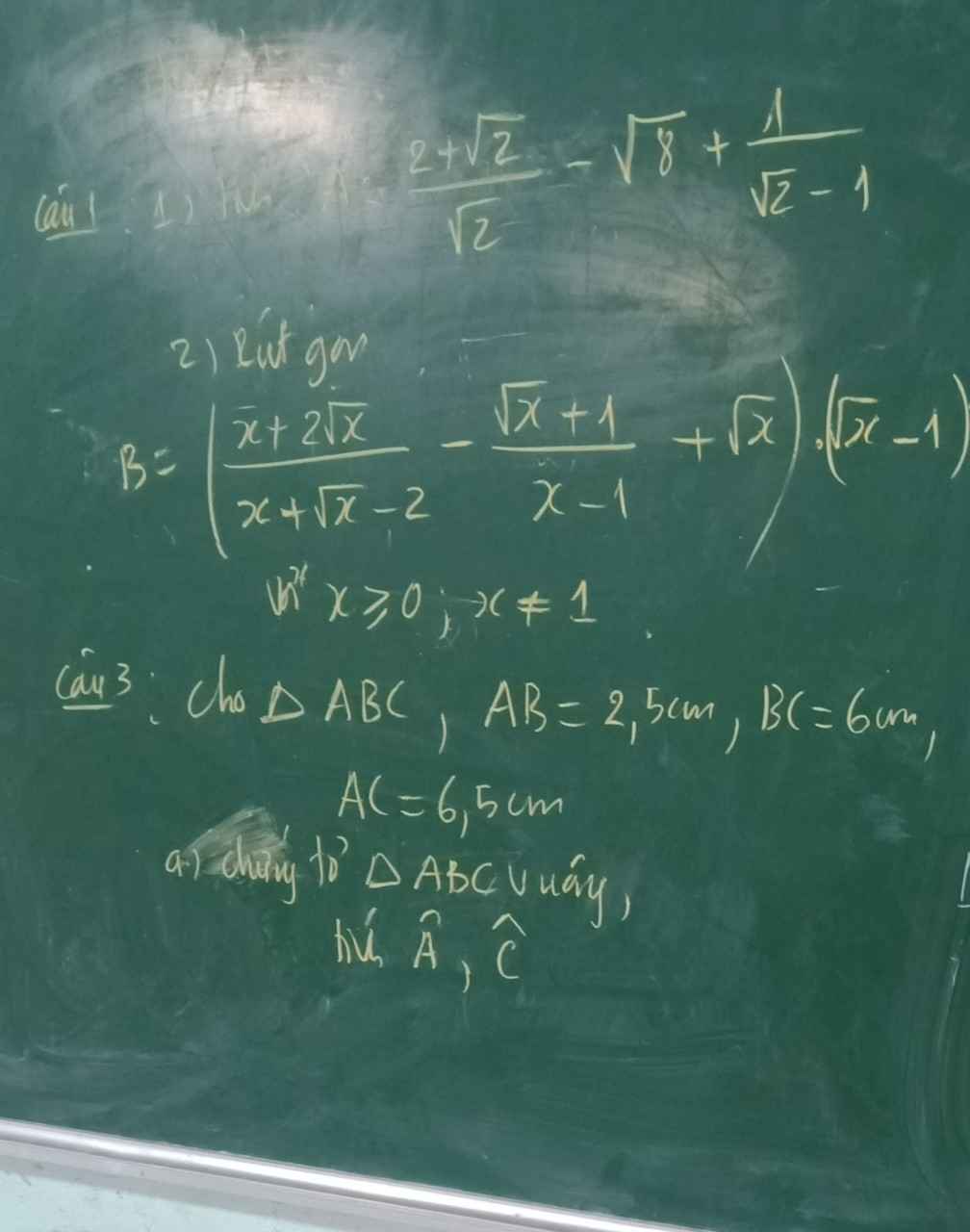Cho tam giác ABC có:AB=3cm;Ac=4cm;BC=5cm.Tính độ dài:AH,BH,CH ?
Đề số 1
AH là đường cao ứng với cạnh BC?
Do \(AB^2+AC^2=25=BC^2\) nên tam giác ABC vuông tại A theo Pitago đảo
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\left(cm\right)\)
\(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{9}{5}\left(cm\right)\)
\(CH=BC-BH=\dfrac{16}{5}\left(cm\right)\)
Đúng 3
Bình luận (1)
Ta có : \(AB^2+AC^2=3^2+4^2=5^2=BC^2\) \(\Rightarrow\Delta ABC\perp\) tại A
Có : \(AH\perp BC\) tại H . Áp dụng HTL ; ta có :
\(AH=\dfrac{AB.AC}{BC}=\dfrac{3.4}{5}=\dfrac{12}{5}\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=\dfrac{3^2}{5}=\dfrac{9}{5}\left(cm\right)\)
\(CH=BC-BH=5-\dfrac{9}{5}=\dfrac{16}{5}\) (cm)
Đúng 2
Bình luận (0)
Câu 1:Giải các pt và hệ pt sau:
1)Giải pt:
a,\(\sqrt{\left(3x-1\right)^2}=2\)
b,(2x+10)(x-4)=0
2)Giải hệ pt:
a,\(\left\{{}\begin{matrix}2x-y=1-2y\\3x+y=3-x\end{matrix}\right.\)
b,\(\left\{{}\begin{matrix}x-y=1\\3x+1=7\end{matrix}\right.\)
1) Giải pt:
a, \(\sqrt{\left(3x-1\right)^2}=2\Leftrightarrow\left|3x-1\right|=2\Leftrightarrow\left[{}\begin{matrix}3x-1=2\\3x-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=3\\3x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{1;-\dfrac{1}{3}\right\}.\)
b, \(\left(2x+10\right)\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}2x+10=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=4\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{-5;4\right\}.\)
2) Giải hệ pt:
a, \(\left\{{}\begin{matrix}2x-y=1-2y\\3x+y=3-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=1\\4x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-2x\\4x+\left(1-2x\right)=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1-2x\\2x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm là: \(\left(x;y\right)=\left(1;-1\right).\)
b, \(\left\{{}\begin{matrix}x-y=1\\3x+1=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=1\\3x=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy hệ phương trình có nghiệm là: \(\left(x;y\right)=\left(2;1\right).\)
Đúng 1
Bình luận (0)
Câu 1:Cho x,y là các số không âm thỏa mãn sqrt{x}+sqrt{y}ge1.Tìm giá trị nhỏ nhất của biểu thức Pdfrac{2x+8sqrt{x}+17}{sqrt{x}+2}+dfrac{3y+6sqrt{y}+5}{sqrt{y}+1}Câu 2:Cho x0,y0 và x+yge6.Tìm giá trị nhỏ nhất của biểu thức:P3x+2y+dfrac{6}{x}+dfrac{8}{y}.Câu 3:Cho biểu thức Pa4+b4-ab,với a,b là các số thực thỏa mãn a2+b2+ab3.Tìm giá trị lớn nhất và nhỏ nhất của P.
Đọc tiếp
Câu 1:Cho x,y là các số không âm thỏa mãn \(\sqrt{x}+\sqrt{y}\ge1\).Tìm giá trị nhỏ nhất của biểu thức P=\(\dfrac{2x+8\sqrt{x}+17}{\sqrt{x}+2}+\dfrac{3y+6\sqrt{y}+5}{\sqrt{y}+1}\)
Câu 2:Cho \(x>0,y>0\) và x+y\(\ge\)6.Tìm giá trị nhỏ nhất của biểu thức:
P=3x+2y+\(\dfrac{6}{x}\)+\(\dfrac{8}{y}\).
Câu 3:Cho biểu thức P=a4+b4-ab,với a,b là các số thực thỏa mãn a2+b2+ab=3.Tìm giá trị lớn nhất và nhỏ nhất của P.
1.
\(P=\dfrac{2\left(\sqrt{x}+2\right)^2+9}{\sqrt{x}+2}+\dfrac{3\left(\sqrt{y}+1\right)^2+2}{\sqrt{y}+1}\)
\(=2\left(\sqrt{x}+2\right)+\dfrac{9}{\sqrt{x}+2}+3\left(\sqrt{y}+1\right)+\dfrac{2}{\sqrt{y}+1}\)
\(=\left(\sqrt{x}+2\right)+\dfrac{9}{\sqrt{x}+2}+2\left(\sqrt{y}+1+\dfrac{1}{\sqrt{y}+1}\right)+\sqrt{x}+\sqrt{y}+3\)
\(P\ge2\sqrt{\dfrac{9\left(\sqrt{x}+2\right)}{\sqrt{x}+2}}+2.2\sqrt{\dfrac{\sqrt{y}+1}{\sqrt{y}+1}}+1+3=14\)
\(P_{min}=14\) khi \(\left(x;y\right)=\left(1;0\right)\)
Đúng 1
Bình luận (0)
2.
\(P=\dfrac{3}{2}\left(x+\dfrac{4}{x}\right)+\dfrac{1}{2}\left(y+\dfrac{16}{y}\right)+\dfrac{1}{2}\left(x+y\right)\)
\(P\ge\dfrac{3}{2}.2\sqrt{\dfrac{4x}{x}}+\dfrac{1}{2}.2\sqrt{\dfrac{16y}{y}}+\dfrac{1}{2}.6=19\)
\(P_{min}=19\) khi \(\left(x;y\right)=\left(2;4\right)\)
3.
Ta có: \(3=a^2+b^2+ab\ge2ab+ab=3ab\Rightarrow ab\le1\)
\(3=a^2+b^2+ab\ge-2ab+ab=-ab\Rightarrow ab\ge-3\)
\(\Rightarrow-3\le ab\le1\)
Từ đó:
\(P=\left(a^2+b^2\right)^2-2a^2b^2-ab=\left(3-ab\right)^2-2a^2b^2-ab\)
\(P=-a^2b^2-7ab+9\)
\(P=-\left(a^2b^2+7ab-8\right)+1=\left(1-ab\right)\left(ab+8\right)+1\ge1\)
\(P_{min}=1\) khi \(a=b=\pm1\)
\(P=-\left(a^2b^2+7ab+12\right)+21=-\left(ab+3\right)\left(ab+4\right)+21\le21\)
\(P_{max}=21\) khi \(\left(a;b\right)=\left(-\sqrt{3};\sqrt{3}\right);\left(\sqrt{3};-\sqrt{3}\right)\)
Đúng 1
Bình luận (0)
a: BC=5cm
AH=3*4/5=2,4cm
HB=3^2/5=1,8cm
HC=5-1,8=3,2cm
b: ΔAHB vuông tại H có HE vuông góc AB
nên AH^2=AE*AB
ΔAHC vuông tại H có HF vuông góc AC
nên AH^2=AF*AC=AE*AB
Đúng 0
Bình luận (0)
Rút gọn biểu thức : B = x√x +x - 9/x - √x - 2 - √x - 1/ √x - 2 + √x - 2/√x + 1 ( x>0, x khác 4 ) - Giải giúp mình với ạ, mình cảm ơn!
Câu 3:
Xét ΔABC có \(AC^2=AB^2+BC^2\)
nên ΔBAC vuông tại B
Xét ΔABC vuông tại B có sin A=BC/AC=6/6,5=12/13
nên góc A=67 độ
=>góc C=23 độ
Đúng 0
Bình luận (0)
Giải Phương Trình 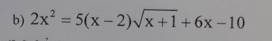
\(\Leftrightarrow2\left(x-2\right)^2-4\left(x-2\right)\sqrt{x+1}-\left(x-2\right)\sqrt{x+1}+2\sqrt{\left(x+1\right)^2}=0\)
=>\(2\left(x-2\right)\left(x-2-2\sqrt{x+1}\right)-\sqrt{x+1}\left(x-2-2\sqrt{x+1}\right)=0\)
=>\(\left(x-2-2\sqrt{x+1}\right)\left(2x-4-\sqrt{x+1}\right)=0\)
=>x(x-8)=0 hoặc 4x^2-17x+15=0
=>x=0(loại);x=8(nhận);x=3(nhận); x=5/4(loại)
S={3;8}
Đúng 0
Bình luận (0)
Câu 1 : giá trị biểu thức sqrt{left(2-sqrt{5}right)^2}+2+sqrt{5} bằng Câu 2 : Cho tam giác ABC vuông tại A , biết BC 10 cm , góc B 30 độ Khi đó độ dài cạnh AC bằng
Đọc tiếp
Câu 1 : giá trị biểu thức \(\sqrt{\left(2-\sqrt{5}\right)^2}+2+\sqrt{5}\) bằng
Câu 2 : Cho tam giác ABC vuông tại A , biết BC = 10 cm , góc B = 30 độ Khi đó độ dài cạnh AC bằng
Câu 1:
\(=\sqrt{5}-2+2+\sqrt{5}=2\sqrt{5}\)
Đúng 0
Bình luận (0)
Trong hình trên tan C bằng :dfrac{CH}{AH} dfrac{AC}{BC} dfrac{AH}{AC} dfrac{AB}{AC}
Đọc tiếp
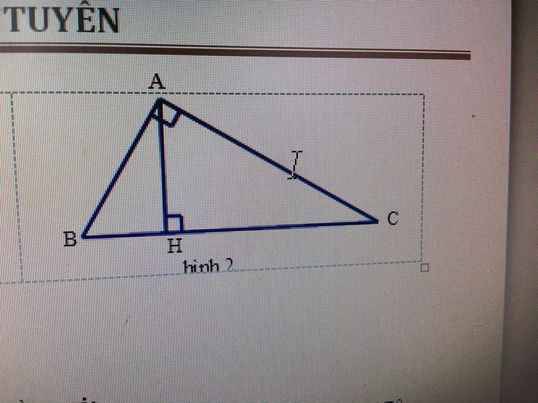 Trong hình trên tan C bằng :
Trong hình trên tan C bằng :
\(\dfrac{CH}{AH}\) \(\dfrac{AC}{BC}\) \(\dfrac{AH}{AC}\) \(\dfrac{AB}{AC}\)
Cho tam giác ABC vuông tại A ,đường cao AH.Gọi E,F lần lượt là hình chiếu của H trên canh AB , AC .
1) Cho AC = 3cm , BC=6cm .Tính AB , góc B , AH , HC
2) Cm : Tứ giác AEHF là hcn và \(EF^2\) = AB*AE
3) CM : EA*EB+AF*FC=HB*HC
![]()
1: \(AB=\sqrt{6^2-3^2}=3\sqrt{3}\left(cm\right)\)
Xét ΔABC vuông tại A có sin B=AC/BC=1/2
nên góc B=30 độ
\(AH=\dfrac{3\cdot3\sqrt{3}}{6}=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
\(HC=\dfrac{3^2}{6}=1.5\left(cm\right)\)
2: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
=>AH=EF
=>\(EF^2=AB\cdot AE\)
Đúng 1
Bình luận (0)